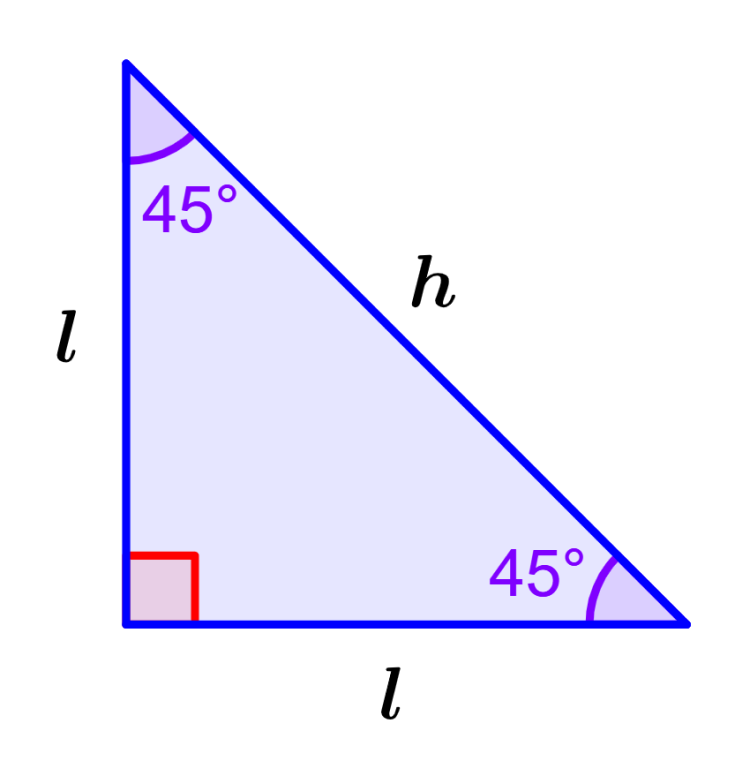
Un triángulo rectángulo es un triángulo en el que exactamente un ángulo interno mide 90 grados. Dado que la suma de los ángulos internos en cualquier triángulo es igual a 180 grados, sabemos que la suma de los otros dos ángulos de un triángulo rectángulo debe ser igual a 90 grados. Los dos lados perpendiculares son llamados los catetos de un triángulo rectángulo y el lado más largo, opuesto al ángulo recto, es llamado la hipotenusa. Un triángulo rectángulo puede ser escaleno (que tiene los tres lados de diferentes longitudes) o isósceles (que tiene dos lados con la misma longitud).
A continuación, miraremos la definición de un triángulo rectángulo isósceles. También, conoceremos sus fórmulas más importantes y las aplicaremos para resolver algunos problemas.
Definición del triángulo rectángulo isósceles
Un triángulo rectángulo isósceles es un triángulo con un ángulo de 90 grados que consiste de dos catetos con longitudes iguales. Dado que los dos catetos tienen longitudes iguales, los ángulos correspondientes serán congruentes (la misma medida).
Entonces, en un triángulo rectángulo isósceles, dos catetos y dos ángulos agudos son congruentes.
Dado que es un triángulo, el ángulo entre los dos catetos medirá 90 grados. Por lo tanto, los catetos serán perpendiculares el uno con el otro.
Fórmulas más usadas del triángulo rectángulo isósceles
La fórmula más importante asociada con triángulos rectángulos es el teorema de Pitágoras. De acuerdo con este teorema, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados del triángulo rectángulo.
En el caso de un triángulo rectángulo isósceles, sabemos que los otros dos lados son iguales en longitud. Entonces, podemos encontrar la hipotenusa usando la siguiente fórmula:
| $latex {{h}^2}={{l}^2}+{{l}^2}$ $latex {{h}^2}=2{{l}^2}$ |
en donde, h es la longitud de la hipotenusa y l es la longitud de los lados.
Área de un triángulo rectángulo isósceles
El área de cualquier triángulo puede ser calculada usando la fórmula $latex A=\frac{1}{2}bh$, en donde b es la longitud de la base del triángulo y h es la longitud de la altura.
Dado que en un triángulo rectángulo isósceles los lados tienen la misma longitud, podemos usar l para representar a la longitud de cada lado y tenemos la fórmula:
| $latex A= \frac{1}{2}l \times l$ $latex A= \frac{1}{2}{{l}^2}$ |
en donde, l es la longitud de uno de los lados congruentes del triángulo.
Perímetro de un triángulo rectángulo isósceles
El perímetro es igual a la suma de las longitudes de todos los lados del triángulo. Entonces, podemos calcular el perímetro de un triángulo usando la fórmula $latex p=a+b+c$, en donde, $latex a,~b,~c$ son las longitudes de los lados.
En un triángulo rectángulo isósceles, sabemos que los lados tienen longitudes congruentes, por lo que tenemos la siguiente fórmula:
| $latex p=h+l+l$ $latex p=h+2l$ |
en donde, h es la longitud de la hipotenusa y l es la longitud de los lados congruentes.
Ejemplos de problemas de triángulos rectángulos isósceles
EJEMPLO 1
- ¿Cuál es la longitud de la hipotenusa de un triángulo que tiene lados congruentes de longitud 5 m?
Solución: Podemos usar el teorema de Pitágoras para encontrar la hipotenusa. Dado que tenemos dos lados congruentes, usamos la siguiente fórmula:
$latex {{h}^2}=2{{l}^2}$
$latex {{h}^2}=2({{5}^2})$
$latex {{h}^2}=2(25)$
$latex {{h}^2}=50$
$latex h=7.07$
La longitud de la hipotenusa es 7.07 m.
EJEMPLO 2
- Un triángulo rectángulo isósceles tiene lados congruentes de longitud 10 m. ¿Cuál es su área?
Solución: Usamos la fórmula modificada del área con el valor $latex l=10$ que es la longitud de los lados congruentes:
$latex A= \frac{1}{2}{{l}^2}$
$latex A= \frac{1}{2}({{10}^2})$
$latex A= \frac{1}{2}(100)$
$latex A=50$
El área del triángulo es 50 m².
EJEMPLO 3
- ¿Cuál es el perímetro de un triángulo que tiene una hipotenusa de 19.8 m y lados congruentes de longitud 14?
Solución: Podemos usar la fórmula del perímetro para resolver esto. Tenemos dos lados congruentes, por lo que usamos la siguiente fórmula:
$latex p=h+2l$
$latex p=19.8+2(14)$
$latex p=19.8+28$
$latex p=47.8$
El perímetro es 47.8 m.
Ejercicios de triángulos rectángulos isósceles para resolver
Véase también
¿Interesado en aprender más sobre triángulos isósceles? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
