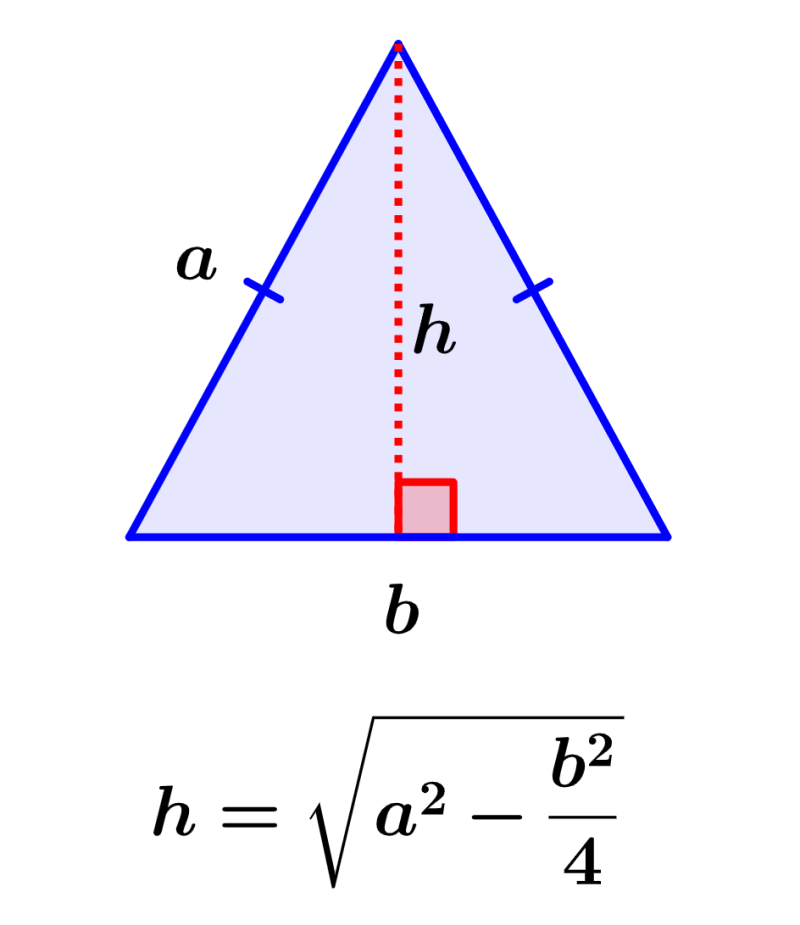
La altura de un triángulo isósceles es la distancia perpendicular desde la base hasta el vértice opuesto. Para calcular la altura, podemos usar el teorema de Pitágoras y derivar una fórmula que depende de la longitud de la base y la longitud de uno de los lados congruentes.
A continuación, aprenderemos a derivar la fórmula de la altura de triángulos isósceles. Además, usaremos esta fórmula para resolver algunos ejercicios de práctica.
Fórmula de la altura de triángulos isósceles
La altura de un triángulo isósceles es calculada usando la longitud de su base y la longitud de unos de los lados congruentes. Podemos calcular la altura usando la siguiente fórmula:
| $latex h= \sqrt{{{a}^2}- \frac{{{b}^2}}{4}}$ |
en donde, a es la longitud de los lados congruentes del triángulo y b es la longitud de la base del triángulo.
Derivación de la fórmula de la altura
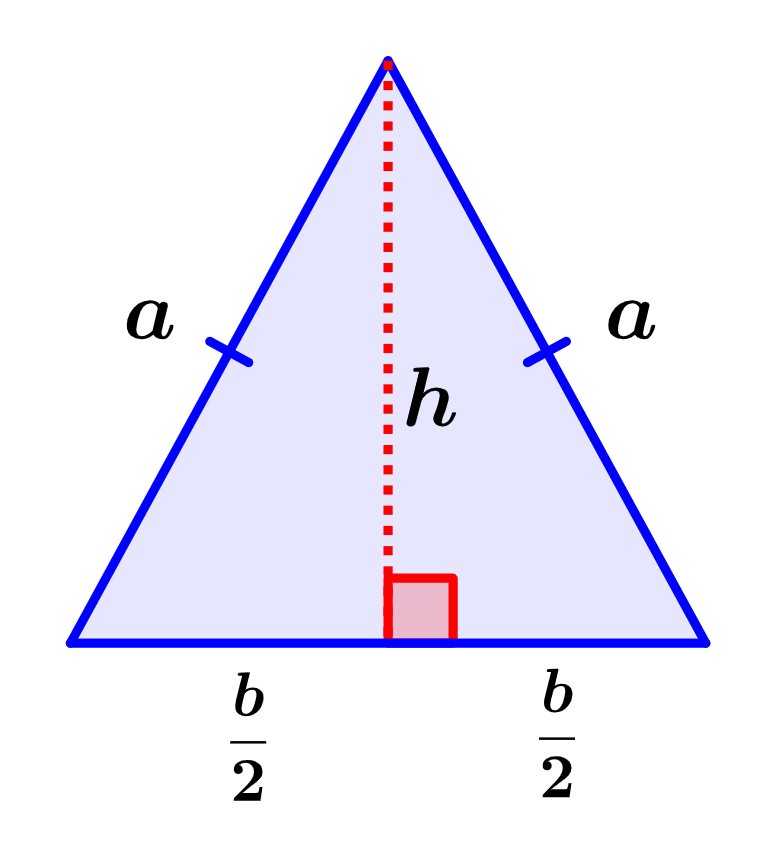
Para derivar esta fórmula, podemos considerar al siguiente triángulo isósceles:
Al trazar una línea que representa a la altura, podemos ver que dividimos al triángulo isósceles en dos triángulos rectángulos congruentes. Podemos usar uno de los triángulos obtenidos y aplicar el teorema de Pitágoras para calcular la altura.
Recordemos que el teorema de Pitágoras nos dice que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. Entonces, tenemos:
$latex {{a}^2}={{h}^2}+{{( \frac{b}{2})}^2}$
$latex {{a}^2}={{h}^2}+ \frac{{{b}^2}}{4}$
$latex {{h}^2}={{a}^2}- \frac{{{b}^2}}{4}$
$latex h= \sqrt{{{a}^2}- \frac{{{b}^2}}{4}}$
Hemos obtenido una expresión para la altura.
Ejercicios de altura de triángulos isósceles resueltos
Los siguientes ejercicios usan la fórmula vista para encontrar la altura de los triángulos isósceles. Intenta resolver los ejercicios tú mismo antes de mirar la solución.
EJERCICIO 1
¿Cuál es la altura de un triángulo isósceles que tiene una base de 8 m y lados congruentes de longitud 6 m?
Solución
De la pregunta, tenemos los siguientes datos:
- Base, $latex b=8$ m
- Lados, $latex a=6$ m
Entonces, usamos la fórmula de la altura con estos valores:
$latex h= \sqrt{{{a}^2}- \frac{{{b}^2}}{4}}$
$latex h= \sqrt{{{6}^2}- \frac{{{8}^2}}{4}}$
$latex h= \sqrt{36- \frac{64}{4}}$
$latex h= \sqrt{36-16}$
$latex h= \sqrt{20}$
$latex h=4.47$
La altura del triángulo es 4.47 m.
EJERCICIO 2
Un triángulo isósceles tiene una base de 10 m y lados congruentes con longitud 12 m. ¿Cuál es la longitud de su altura?
Solución
Podemos identificar la siguiente información:
- Base, $latex b=10$ m
- Lados, $latex a=12$ m
Reemplazando estos valores en la fórmula, tenemos:
$latex h= \sqrt{{{a}^2}- \frac{{{b}^2}}{4}}$
$latex h= \sqrt{{{12}^2}- \frac{{{10}^2}}{4}}$
$latex h= \sqrt{144- \frac{100}{4}}$
$latex h= \sqrt{144-25}$
$latex h= \sqrt{119}$
$latex h=10.91$
La altura del triángulo es 10.91 m.
EJERCICIO 3
Un triángulo isósceles tiene una base de longitud 8 m y lados congruentes de longitud 9 m. ¿Cuál es la longitud de la altura?
Solución
De la pregunta, tenemos los siguientes datos:
- Base, $latex b=8$ m
- Lados, $latex a=9$ m
Sustituyendo estos valores en la fórmula de la altura, tenemos:
$latex h= \sqrt{{{a}^2}- \frac{{{b}^2}}{4}}$
$latex h= \sqrt{{{9}^2}- \frac{{{8}^2}}{4}}$
$latex h= \sqrt{81- \frac{64}{4}}$
$latex h= \sqrt{81-16}$
$latex h= \sqrt{65}$
$latex h=8.06$
La altura del triángulo es 8.06 m.
EJERCICIO 4
¿Cuál es la altura de un triángulo que tiene una base de longitud 14 m y lados congruentes de longitud 11 m?
Solución
Tenemos la siguiente información:
- Base, $latex b=14$ m
- Lados, $latex a=11$ m
Entonces, usamos la fórmula de la altura con estos valores:
$latex h= \sqrt{{{a}^2}- \frac{{{b}^2}}{4}}$
$latex h= \sqrt{{{11}^2}- \frac{{{14}^2}}{4}}$
$latex h= \sqrt{121- \frac{196}{4}}$
$latex h= \sqrt{121-49}$
$latex h= \sqrt{72}$
$latex h=8.49$
La altura del triángulo es 8.49 m.
Ejercicios de altura de triángulos isósceles para resolver
Usa la fórmula de la altura de triángulos isósceles para resolver los siguientes problemas. Si es que necesitas ayuda, puedes mirar los ejercicios resueltos de arriba.
Véase también
¿Interesado en aprender más sobre triángulos isósceles? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
