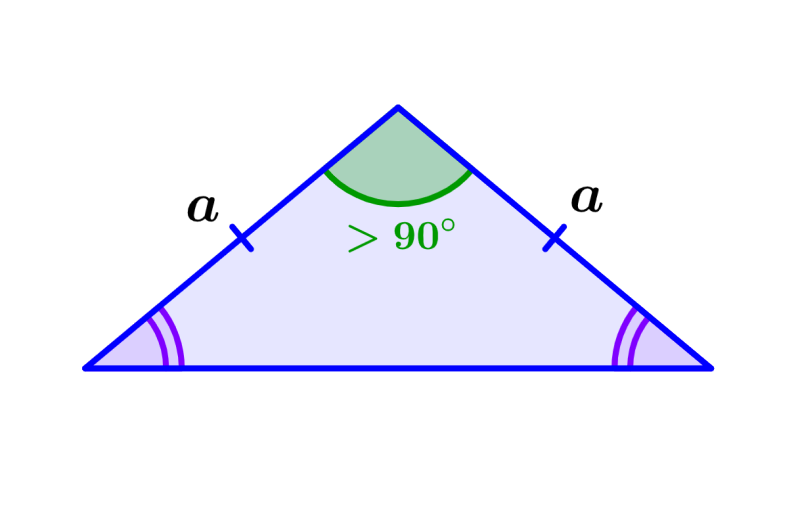
Los triángulos isósceles obtusángulos son triángulos que tienen dos lados con la misma longitud y un ángulo mayor que 90 grados. Estos triángulos cumplen con las condiciones de un triángulo isósceles y un triángulo obtusángulo al mismo tiempo. Recordemos que un triángulo isósceles tiene dos lados que tienen la misma longitud y dos ángulos que tienen la misma medida. Por otra parte, un triángulo obtusángulo se caracteriza por tener un ángulo interno que mide más de 90 grados.
A continuación, conoceremos las características más importantes de este tipo de triángulos. También, haremos una revisión de las fórmulas más útiles y las aplicaremos para resolver algunos ejercicios.
Características de los triángulos isósceles obtusángulos
Los triángulos isósceles obtusángulos tienen las siguientes características:
- Dos lados del triángulo son congruentes (tienen igual longitud).
- El lado que no tiene la misma longitud es llamado la base del triángulo.
- Un ángulo interno del triángulo es obtuso, es decir, tiene más de 90 grados.
- Los ángulos opuestos a los lados iguales también son iguales y agudos.
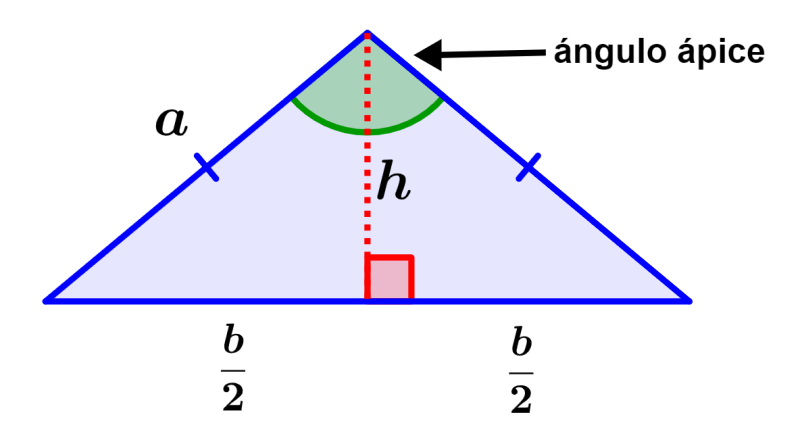
- El ángulo diferente a los otros dos es llamado ángulo ápice.
- El ángulo ápice es el ángulo obtuso.
- La altura es la línea perpendicular a la base y que une al ángulo ápice.
- La altura divide a la base en dos partes iguales, así como también al ángulo ápice.
- La altura divide al triángulo en dos triángulos rectángulos congruentes.
Fórmulas más usadas de triángulos isósceles
Con las siguientes fórmulas, podemos resolver una gran cantidad de problemas relacionados a triángulos isósceles.
Fórmula del perímetro de triángulos isósceles
El perímetro de cualquier figura geométrica es calculado al sumar las longitudes de los lados de la figura. La fórmula del perímetro de triángulos isósceles considera el hecho que dos lados del triángulo son iguales:
| $latex p=b+2a$ |
en donde, b es la longitud de la base y a es la longitud de los lados congruentes.
Fórmula del área de triángulos isósceles
La fórmula para calcular el área de cualquier triángulo es la siguiente:
| $latex A= \frac{1}{2} \times b \times h$ |
en donde, b representa a la longitud de la base y h representa a la longitud de la altura.
Fórmula de la altura de triángulos isósceles
La fórmula de la altura es derivada del teorema de Pitágoras, en donde usamos las longitudes de la base y de los lados congruentes:
| $latex h= \sqrt{{{a}^2}- \frac{{{b}^2}}{4}}$ |
en donde, a es la longitud de los lados congruentes y b es la longitud de la base.
Ejemplos resueltos de problemas de triángulos isósceles
EJEMPLO 1
- Un triángulo isósceles tiene una base de longitud 15 m y sus lados congruentes miden 12 m. ¿Cuál es su perímetro?
Solución: De la pregunta, obtenemos los siguientes valores:
- Base, $latex b=15$ m
- Lados, $latex a=12$ m
Usando la fórmula del perímetro, tenemos:
$latex p=b+2a$
$latex p=15+2(12)$
$latex p=15+24$
$latex p=39$
El perímetro es 39 m.
EJEMPLO 2
- ¿Cuál es el área de un triángulo que tiene una base de 20 m y una altura de 15 m?
Solución: Reconocemos los siguientes valores:
- Base, $latex b=20$ m
- Altura, $latex h=15$ m
Usamos la fórmula del área con estos valores:
$latex A= \frac{1}{2}bh$
$latex A= \frac{1}{2}(20)(15)$
$latex A=150$
El área es 150 m².
EJEMPLO 3
- Un triángulo isósceles tiene una base de longitud 16 m y lados congruentes de longitud 10 m. ¿Cuál es su altura?
Solución: Tenemos los siguientes valores:
- Base, $latex b=16$ m
- Lados, $latex a=10$ m
Usamos la fórmula de la altura con estos valores:
$latex h= \sqrt{{{a}^2}- \frac{{{b}^2}}{4}}$
$latex h= \sqrt{{{10}^2}- \frac{{{16}^2}}{4}}$
$latex h= \sqrt{100- \frac{256}{4}}$
$latex h= \sqrt{100-64}$
$latex h= \sqrt{36}$
$latex h=6$
La altura del triángulo es 6 m.
Ejercicios de triángulos isósceles para resolver
Véase también
¿Interesado en aprender más sobre triángulos isósceles? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
