Las secciones transversales de un cubo son figuras bidimensionales obtenidas por la intersección de un plano con un cubo. Dependiendo de la orientación del plano, podemos obtener secciones transversales cuadradas, rectangulares, triangulares y hexagonales.
A continuación, aprenderemos sobre las secciones transversales de un cubo detalladamente usando diagramas.
Sección transversal cuadrada
Cuando cortamos a un cubo con un plano que es paralelo a cualquiera de sus seis caras, la sección transversal formada es cuadrada.
Un cubo tiene todos sus lados con la misma longitud. Esto significa que las seis caras del cubo tienen la misma forma y la misma área. Entonces, el área de una sección transversal cuadrada de un cubo es igual al área de una de las caras.
EJEMPLO
Si es que un cubo tiene lados de 5 m, ¿cuál es el área de su sección transversal cuadrada?.
Solución: Sabemos que el área de la sección transversal cuadrada es igual al área de una de las caras del cubo. Entonces, solo tenemos que encontrar el área de una cara del cubo.
El área de un cuadrado es igual a A=l², en donde, l es la longitud de uno de los lados del cuadrado. Entonces, tenemos:
A=l²
A=5²
A=25 m²
Sección transversal rectangular
Cuando cortamos a un cubo con un plano que cruza por las diagonales de las caras, obtenemos una sección transversal rectangular.
Podemos encontrar el área de esta sección transversal rectangular usando la longitud de uno de los lados como la altura del rectángulo y la longitud de la diagonal de las caras del cubo como la base del rectángulo. Luego, simplemente multiplicamos estas dos longitudes para obtener el área.
EJEMPLO
Encuentra el área de la sección rectangular formada por las diagonales de las caras de un cubo que tiene lados de 10 m.
Solución: Para encontrar el área de la sección transversal, tenemos que encontrar la longitud de la diagonal de una cara del cubo. Para esto usamos el teorema de Pitágoras, en donde los catetos son dos lados del cubo y la hipotenusa es la diagonal de la cara del cubo:
$latex c^2=a^2+b^2$
$latex c^2=10^2+10^2$
$latex c^2=100+100$
$latex c^2=200$
$latex c=\sqrt{200}$
$latex c=10~\sqrt{2}$
Ahora, multiplicamos esa longitud por la longitud de uno de los lados del cubo y tenemos $latex A=100~\sqrt{2}$ m².
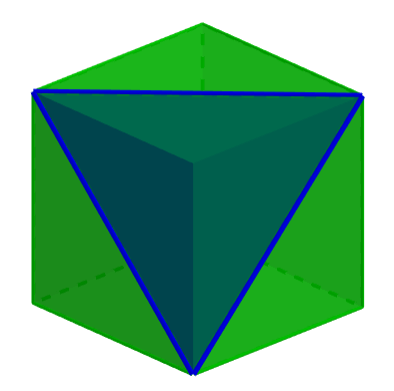
Sección transversal triangular
Las secciones transversales cuadrada y rectangular son formadas cuando intersecamos a un cubo con planos paralelos a las caras del cubo. Sin embargo, también podemos obtener diferentes secciones transversales cuando cortamos a un cubo con un plano que tiene una inclinación con respecto a su base.
Por ejemplo, cuando el plano interseca a tres aristas del cubo, obtenemos una sección transversal triangular. Si es que el plano interseca a tres vértices del cubo, obtenemos un triángulo equilátero.
Sección transversal hexagonal
Cuando un plano interseca a un cubo en los puntos medios de seis de sus aristas, obtenemos una sección transversal hexagonal regular como se muestra en el diagrama.
También podemos obtener hexágonos irregulares cuando inclinamos al plano para que interseque en seis aristas fuera de los puntos medios.
Véase también
¿Interesado en aprender más sobre secciones transversales? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
