Las secciones transversales de una esfera son figuras bidimensionales formadas por la intersección de un plano con una esfera. Dado que la esfera tiene una forma completamente redonda con un radio constante, cualquier plano que corte a una esfera formará una sección transversal circular sin importar la inclinación del plano.
A continuación, conoceremos más detalles sobre las secciones transversales de una esfera. Usaremos diagramas y ejemplos.
Secciones transversales circulares
Una esfera es una figura tridimensional perfectamente redonda, la cual tiene un radio constante en todas las direcciones. Esto significa que, cuando cortamos a una esfera con un plano, siempre obtendremos una sección transversal circular independientemente de la inclinación del plano.
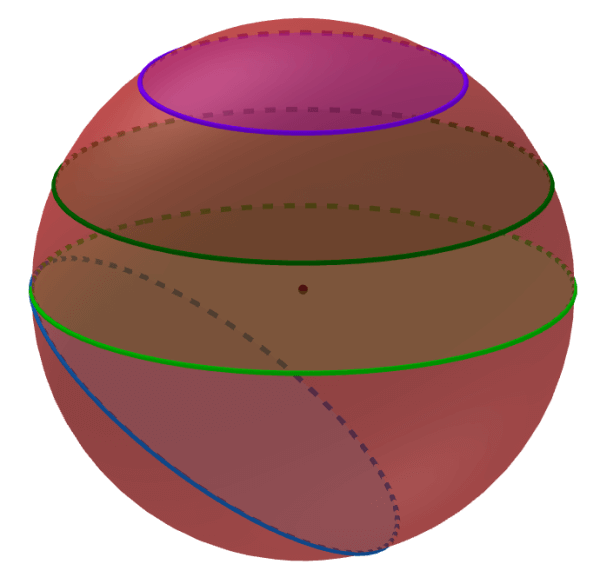
Dependiendo de la orientación del plano que corta a la esfera, podemos tener tres tipos de secciones transversales:
- Sección transversal horizontal
- Sección transversal vertical
- Sección transversal inclinada
Sin embargo, como ya lo hemos mencionado, todas las secciones transversales de una esfera serán circulares.
Área de la sección transversal de una esfera
Dado que la sección transversal es una figura bidimensional, podemos calcular su área si es que tenemos algo de información de la figura. Por ejemplo, si es que conocemos el radio de la esfera y sabemos que la sección transversal cruza por el centro, podemos usar la fórmula del área de un círculo con el radio de la esfera.
Además, podemos calcular el área de cualquier sección transversal de una esfera si es que conocemos su radio.
EJEMPLO 1
Encuentra el área de la sección transversal que pasa por el centro de una esfera que tiene un radio de 5 m.
Solución: Dado que la sección transversal pasa por el centro de la esfera, sabemos que la sección tendrá el mismo diámetro y el mismo radio que la esfera. Entonces, podemos usar la fórmula del área de un círculo con el radio dado.
A=πr²
A=π(5)²
A=25π m²
EJEMPLO 2
¿Cuál es el área de una sección transversal de una esfera con un radio de 8 m?.
Solución: Nuevamente, solo tenemos que usar la fórmula del área del círculo con el radio dado.
A=πr²
A=π(8)²
A=64π m²
Véase también
¿Interesado en aprender más sobre secciones transversales? Mira estas páginas:


