Una función inversa es una función que revierte el efecto de la función original. La tangente inversa es una función que revierte el efecto de la función tangente. Sabemos que con la función tangente, podemos calcular el lado opuesto si es que conocemos el lado adyacente y el ángulo de un triángulo rectángulo. Con la función tangente inversa, podemos encontrar la medida de un ángulo si es que conocemos las medidas del lado opuesto y del lado adyacente.
A continuación, aprenderemos a usar la función tangente inversa y la aplicaremos para resolver algunos ejercicios de práctica.
¿Cómo encontrar la tangente inversa?
Para encontrar la tangente inversa, tenemos que encontrar el ángulo que resultaría en el número deseado si es que obtenemos su tangente. Por ejemplo, si es que queremos encontrar la tangente inversa de 1, tenemos que preguntarnos «¿cuál ángulo tiene una tangente de 1?». La respuesta es 45°, por lo que concluimos que la tangente inversa de 1 es 45°.
Usamos la notación $latex {{\tan}^{-1}}$ para representar a la tangente inversa. Ten en cuenta que en este caso, el «-1» no indica un recíproco, sino que indica que la función es inversa. Usando esta notación, tendríamos $latex {{\tan}^{-1}}(1)=45$°.
En realidad, existen más ángulos que tienen una tangente igual a 1. Sin embargo, lo que estamos preguntando es «¿cuál es el ángulo más simple que tiene una tangente igual a 1?» La respuesta es 45°. Entonces, tenemos $latex {{\tan}^{-1}}(1)=45$° o en radianes, tenemos $latex {{\tan}^{-1}}(1)=\frac{\pi}{4}$.
La función tangente inversa también es conocida como la función arco tangente y podemos usar la notación «arctan(x)» para representarla.
Gráfica de la función tangente inversa
Una función inversa se caracteriza porque las coordenadas en x y las coordenadas en y de la función se intercambian. Esto significa que en la función tangente inversa, los valores de x corresponden a los valores de y de la función tangente y los valores de y corresponden a los valores de x.
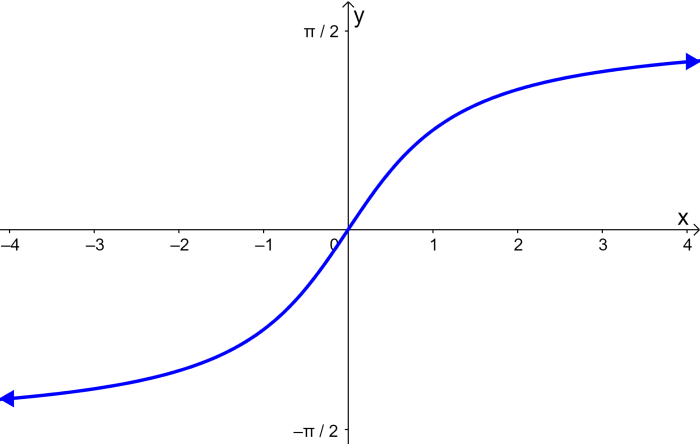
El dominio de la función tangente inversa es igual a todos los números reales. Esto significa que podemos usar cualquier número en la entrada o variable independiente (usualmente x).
El rango de la función tangente inversa es igual a todos los números reales dentro de $latex -90^{\circ} <y<90^{\circ} $ o en radianes, $latex -\frac{\pi}{2}<y<\frac{\pi}{2}$. Esto significa que el ángulo resultante de la tangente inversa tiene que estar dentro de este rango.
Ejercicios de tangente inversa resueltos
Los siguientes ejercicios pueden ser usados para aprender sobre las aplicaciones de la tangente inversa. Cada ejercicio tiene su respectiva solución, pero intenta resolver los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
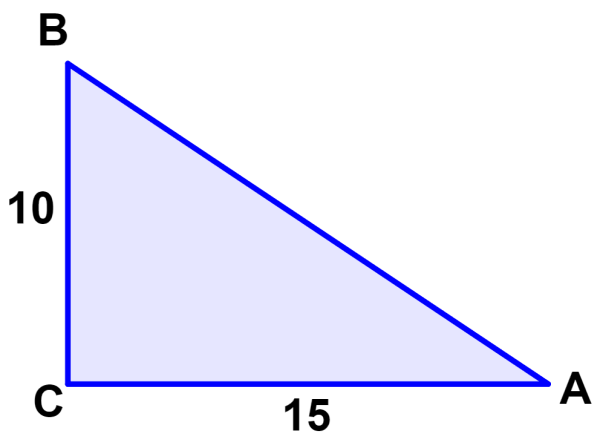
Usa los lados del triángulo y una calculadora para encontrar la medida del ángulo ∠A.
Solución
Podemos ver que en referencia al ángulo ∠A, tenemos las medidas del lado opuesto y el lado adyacente. Entonces, podemos formar una relación con la tangente:
$latex \tan(A)=\frac{\text{opuesto}}{\text{adyacente}}$
$latex \tan(A)=\frac{10}{15}$
Si es que usamos la función tangente inversa, podemos escribir:
$latex {{\tan}^{-1}}(\frac{10}{15})=A$
$latex A=33.7$°
El ángulo A mide 33.7°.
EJERCICIO 2
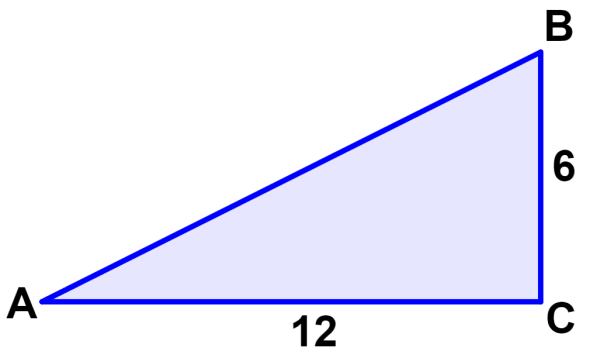
¿Cuál es el valor del ángulo A en el siguiente triángulo?
Solución
Con respecto al ángulo ∠A, conocemos al lado opuesto y al lado adyacente, por lo que usamos la tangente para formar la siguiente ecuación:
$latex \tan(A)=\frac{\text{opuesto}}{\text{adyacente}}$
$latex \tan(A)=\frac{6}{12}$
Al usar la función tangente inversa y una calculadora, tenemos:
$latex {{\tan}^{-1}}(\frac{6}{12})=A$
$latex A=26.6$°
El ángulo A mide 26.6°.
EJERCICIO 3
¿Cuál es la medida del ángulo B?
Solución
En referencia al ángulo ∠B, tenemos las longitudes del lado opuesto y del lado adyacente, por lo que usamos la tangente para encontrar la siguiente relación:
$latex \tan(B)=\frac{\text{opuesto}}{\text{adyacente}}$
$latex \tan(B)=\frac{12}{6}$
Ahora, usamos la tangente inversa para obtener lo siguiente usando una calculadora:
$latex {{\tan}^{-1}}(\frac{12}{6})=B$
$latex B=63.4$°
El ángulo B mide 63.4°.
Véase también
¿Interesado en aprender más sobre tangentes? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
