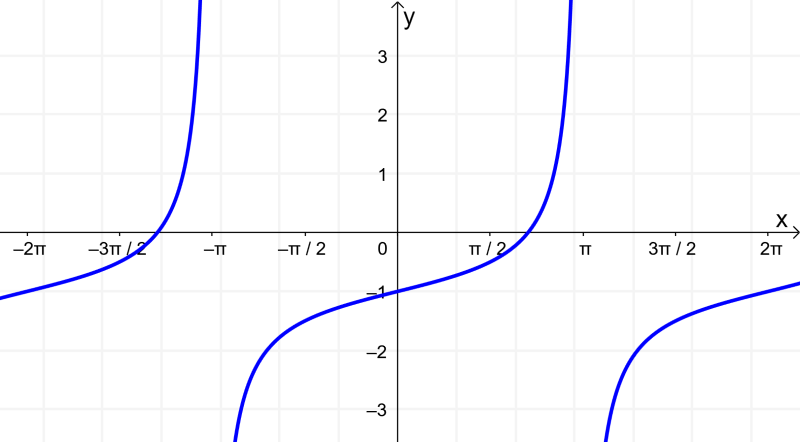
La gráfica de la tangente se ve diferente en comparación con las gráficas del seno y del coseno. A diferencia del dominio del seno y del coseno, el dominio de la tangente no es igual a todos los números reales. La tangente es equivalente al seno sobre el coseno. Por lo tanto, cuando los valores del coseno son iguales a 0, la tangente tiende a infinito. Esto significa que la tangente tiene asíntotas cuando los valores del coseno son 0. Por otra parte, el rango de la tangente sí es igual a todos los números reales.
A continuación, conoceremos cómo graficar la función tangente básica y aprenderemos sobre las variaciones que podemos realizar para modificar su gráfica.
TRIGONOMETRÍA
Relevante para…
Aprender sobre la gráfica de la función tangente con ejercicios.
TRIGONOMETRÍA
Relevante para…
Aprender sobre la gráfica de la función tangente con ejercicios.
Gráfica de la función tangente básica
Recordemos que podemos escribir a la tangente en términos del seno y del coseno: $latex \tan(x)=\frac{\sin(x)}{\cos(x)}$. Esto significa que la tangente será igual a cero cuando el numerador (el seno) es igual a cero. Esto sucede en 0, π, 2π, 3π, etc, y en -π, -2π, -3π, etc.
La tangente será indefinida cada vez que el denominador (el coseno) es cero. Un cero en el denominador significa que tenemos una asíntota vertical.
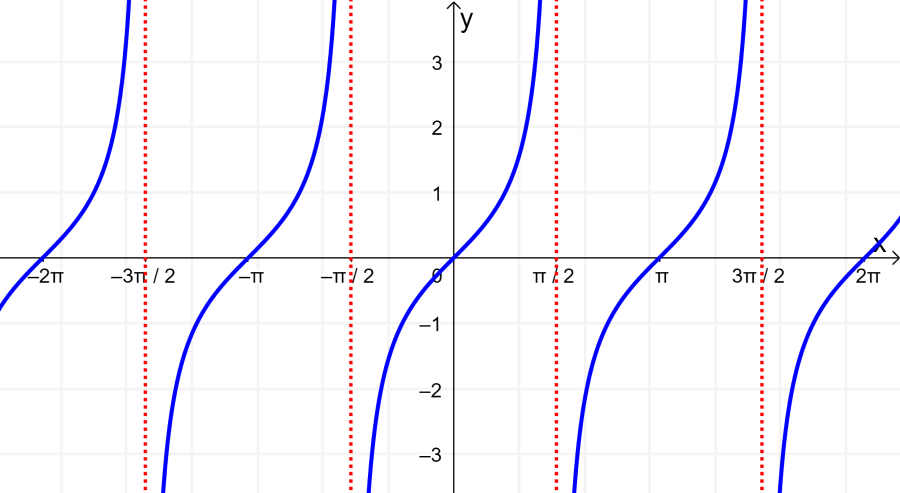
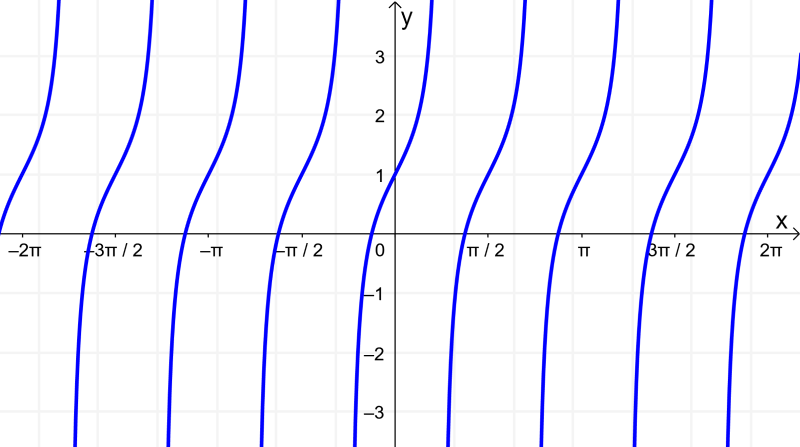
Entonces, la gráfica de la tangente tendrá asíntotas verticales cada vez que el coseno es cero: en -π/2, π/2, 3π/2, etc. Luego, podemos usar un valor que se encuentre en cada porción del eje x para determinar la posición de la gráfica. La gráfica es trazada tomando en cuenta que nunca cruza a las asíntotas.
En la gráfica, vemos que la función se repite en intervalos regulares de π. Esto significa que el periodo de la tangente es π.
Dominio de la función tangente
La función tangente tiene un patrón que se repite indefinidamente tanto hacia el lado x positivo como hacia el lado x negativo. Sin embargo, la tangente puede ser escrita como $latex \tan(x)=\frac{\sin(x)}{\cos(x)}$ y sabemos que no podemos tener al cero en el denominador, por lo que cada vez que tengamos $latex \cos(x)=0$, la función es indefinida.
Esto sucede cuando tenemos múltiplos de $latex \frac{\pi}{2}$. Entonces, el dominio es todos los números reales a excepción de los múltiplos de $latex \frac{\pi}{2}$.
Rango de la función tangente
La gráfica de la función tangente claramente nos muestra que la función puede resultar en cualquier valor de y. Esto significa que el rango es igual a todos los números reales.
Gráficas de variaciones de la función tangente
La gráfica de la función tangente básica puede ser modificada para obtener diferentes variaciones. Podemos modificarla cambiando los diferentes parámetros de la forma general de la tangente. La forma general de la función tangente es:
$latex y=A~\tan(Bx-C)+D$
Cada uno de los parámetros de la función tangente afecta a diferentes características de la gráfica resultante.
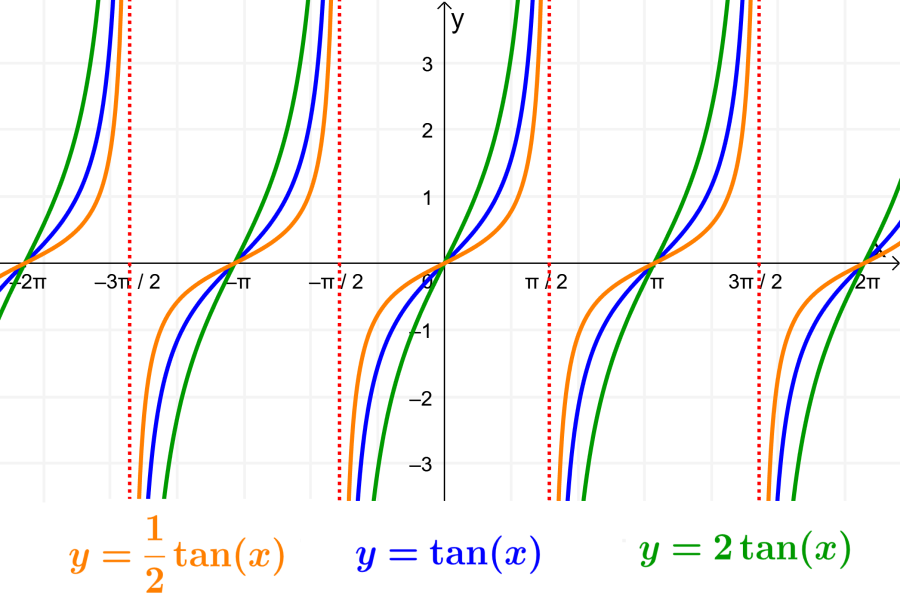
Determinar el estiramiento vertical de la función tangente
El estiramiento vertical representa al cambio en los valores de y de la función con respecto a la función original. Usando la forma general de la tangente, el factor por el que la función es estirada verticalmente es encontrada usando |A|. Si es que A es mayor que 1, la gráfica es estirada y si es que A está entre 0 y 1, la gráfica es comprimida.
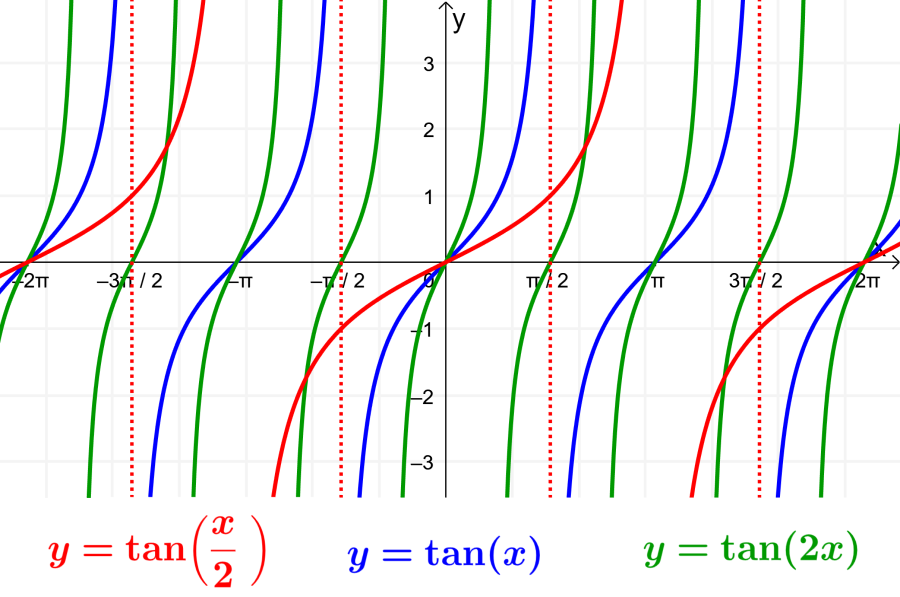
Determinar al periodo de la función tangente
El periodo de la función tangente representa al intervalo después del cual la función se repite. El periodo de la función tangente básica es π.
El parámetro B en la forma general afecta al periodo de la función. Podemos determinar el periodo usando la ecuación $latex P=\frac{\pi}{|B|}$. Cuando el valor de B es mayor que 1, la función es «acelerada» y el periodo es menor que π, por lo que la función es comprimida horizontalmente.
Cuando el valor de B es menor que 1, la función es «desacelerada» y el periodo es mayor que π, por lo que la función es estirada horizontalmente.
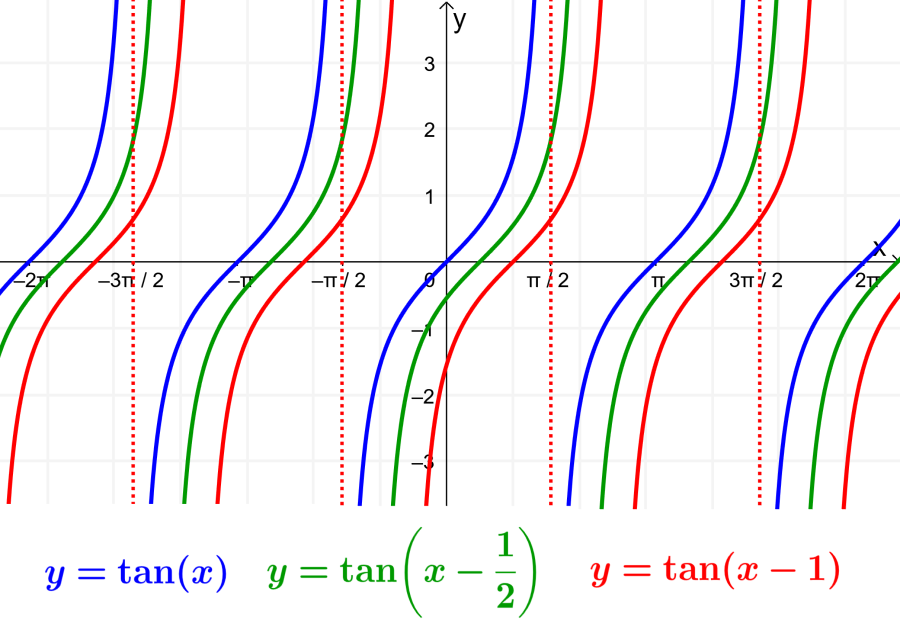
Determinar la fase de la función tangente
La fase representa al desplazamiento horizontal de la función con respecto a la función tangente básica.
Para determinar la fase de la función, reescribimos a la forma general de la función de la siguiente forma: $latex y=A~\tan(B(x-\frac{C}{B})+D$. En esta forma, la fase es igual a $latex \frac{C}{B}$. La gráfica es desplazada hacia la derecha cuando C>0. La gráfica es desplazada hacia la izquierda cuando C<0.
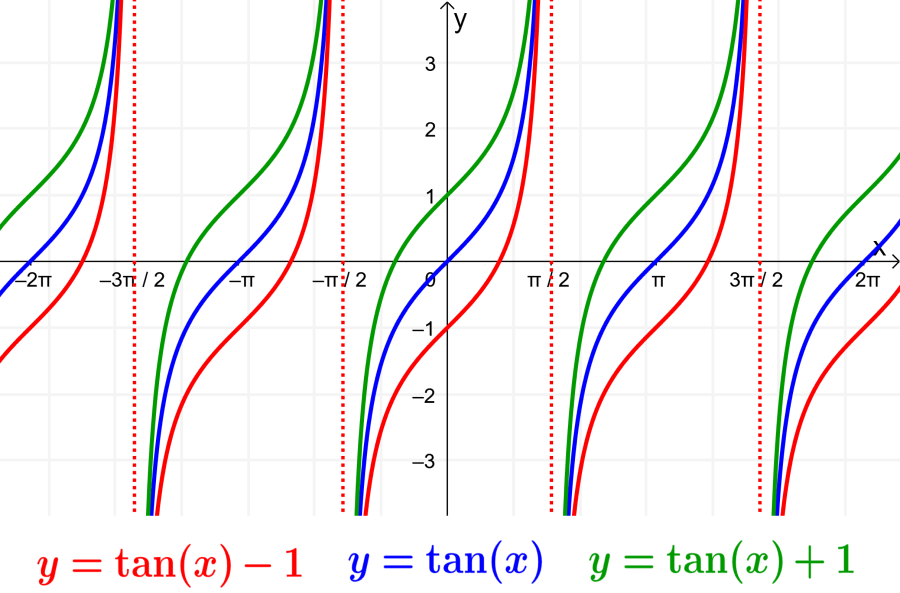
Determinar el desplazamiento vertical de la función tangente
El desplazamiento vertical es determinado por el valor de D en la forma general de la función tangente. Si es que tenemos un valor positivo de D, la gráfica es desplazada hacia arriba. Si es que tenemos un valor negativo de D, la gráfica es desplazada hacia abajo.
Ejercicios de gráficas de tangentes resueltos
Los siguientes ejercicios son resueltos usando lo aprendido sobre las gráficas de las tangentes y sus diferentes parámetros. Intenta resolver los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
¿Cuál es la gráfica de la función $latex y=\tan(2x)+1$?
Solución
Para graficar a esta función, podemos compararla con la forma general para obtener los diferentes parámetros y los efectos que tendrán en la gráfica de la función tangente básica:
- Estiramiento vertical: $latex |A|=1$. La gráfica básica no es afectada.
- Periodo: $latex P=\frac{\pi}{|B|}=\frac{\pi}{2}$. El periodo es la mitad de la gráfica básica. Esto significa que la gráfica estará comprimida horizontalmente.
- Fase: $latex \frac{C}{B}=0$. La función no es desplazada horizontalmente.
- Traslación vertical: $latex D=1$. La gráfica es desplazada verticalmente por 1 unidad.
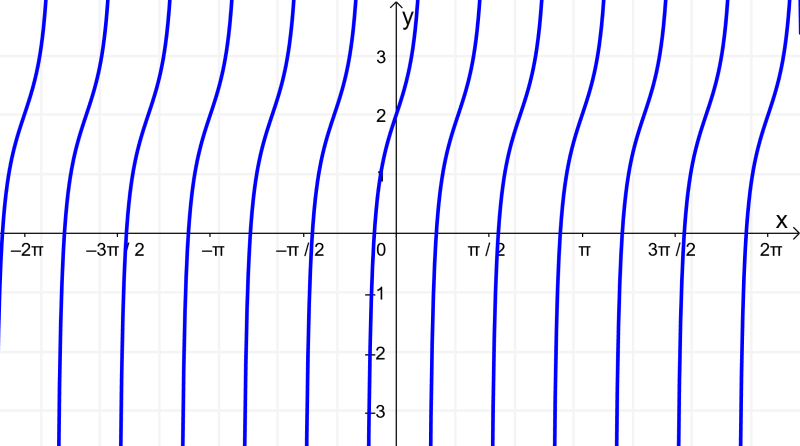
Usando esto, podemos obtener la gráfica de la función:
EJERCICIO 2
Si es que tenemos la función $latex y=2\tan(\frac{1}{2}x-1)-1$, ¿cuál es su gráfica?
Solución
Podemos usar la forma general para obtener los diferentes parámetros y la siguiente información:
- Estiramiento vertical: $latex |A|=2$. La gráfica es estirada verticalmente por un factor de 2.
- Periodo: $latex P=\frac{\pi}{|B|}=\frac{\pi}{\frac{1}{2}}=2\pi$. Eso es el doble del periodo de la función básica, por lo que la gráfica estará estirada horizontalmente.
- Fase: $latex \frac{C}{B}=\frac{1}{\frac{1}{2}}=2$. La gráfica es movida 2 unidades hacia la derecha.
- Traslación vertical: $latex D=-1$. La gráfica es desplazada 1 unidad hacia abajo.
Aplicando estas transformaciones a la función tangente básica, tenemos:
EJERCICIO 3
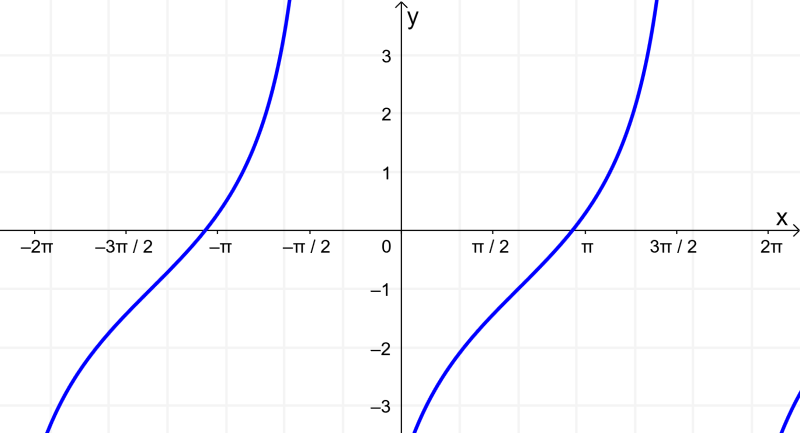
¿Cuál es la ecuación de la siguiente función tangente?
Solución
Podemos extraer la siguiente información de la gráfica:
- La gráfica no está estirada ni comprimida verticalmente. Esto significa que $latex A=1$.
- La gráfica tiene un periodo de $latex \frac{\pi}{3}$. Entonces, el parámetro B debe ser 3.
- La gráfica no tiene ningún desplazamiento horizontal, por lo que C debe ser 0.
- La gráfica está desplazada 2 unidades hacia arriba, por lo que D es igual a 2.
Podemos determinar que la ecuación de esta gráfica es:
$latex y=\tan(3x)+2$
EJERCICIO 4
¿Cuál es la ecuación de la siguiente función tangente?
Solución
Podemos obtener la siguiente información al mirar a la gráfica de la función:
- La gráfica está comprimida verticalmente. Comparando con la función tangente básica, los valores de y son la mitad, por lo que $latex A=\frac{1}{2}$.
- El periodo de la función es 2π, por lo que tenemos $latex B=\frac{1}{2}$.
- No tenemos ningún desplazamiento horizontal, por lo que C debe ser 0.
- La gráfica está desplazada 1 unidad hacia abajo, por lo que D es igual a -1.
Usando esto, concluimos que la ecuación de la gráfica es:
$latex y=\frac{1}{2}\tan(\frac{1}{2}x)-1$
Véase también
¿Interesado en aprender más sobre tangentes? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
