La tangente de un ángulo puede ser definida usando a un triángulo rectángulo. La tangente es igual a la longitud del lado opuesto al ángulo dividida por la longitud del lado adyacente. A pesar de que la tangente es definida con los ángulos de un triángulo rectángulo, la función tangente puede ser usada para cualquier ángulo.
A continuación, aprenderemos más sobre la tangente de un ángulo. Conoceremos los valores de la tangente de ángulos importantes y resolveremos algunos ejercicios de práctica.
Definición de la tangente de un ángulo
El seno y el coseno no son las únicas funciones trigonométricas frecuentemente usadas. La tangente de un ángulo es otra función trigonométrica muy importante. La tangente es definida en términos del círculo unitario.
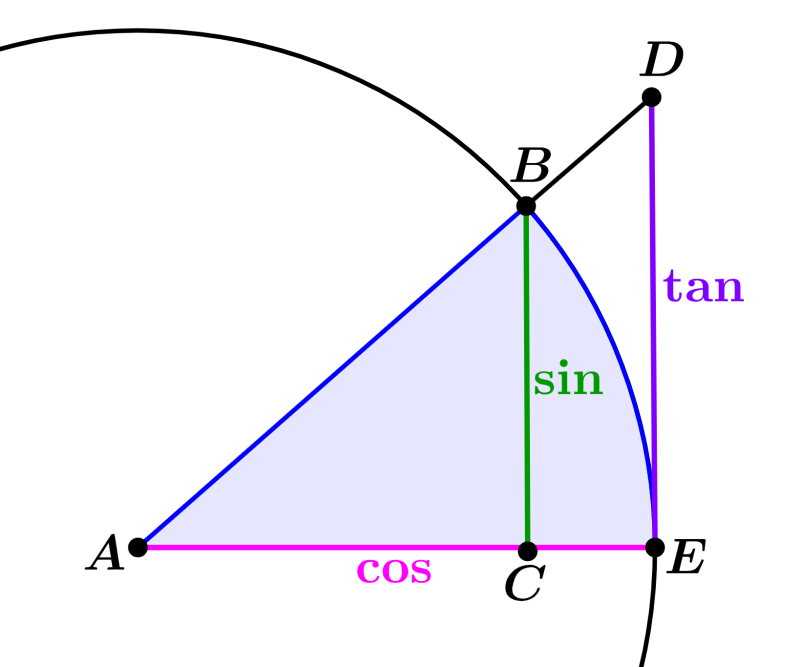
En el siguiente diagrama, la tangente es la longitud de la línea vertical ED que es tangente desde el punto de tangencia, E, hasta el punto D en donde la línea tangente corta al rayo AD formado por el ángulo.
Tangentes en términos de seno y coseno
Los triángulos ABC y ADE del diagrama de arriba son semejantes, por lo que las proporciones de sus lados son iguales. Esto significa que tenemos:
$latex \frac{ED}{AE}=\frac{CB}{AC}$
Mirando al diagrama, vemos que tenemos $latex EA=\tan(A)$. Usamos al círculo unitario, por lo que tenemos $latex AE=1$. Además, también tenemos las relaciones $latex CB=\sin(A)$ y $latex AC=\cos(A)$. Usando esto, encontramos la identidad fundamental:
| $latex \tan(A)=\frac{\sin(A)}{\cos(A)}$ |
Triángulos rectángulos y tangentes
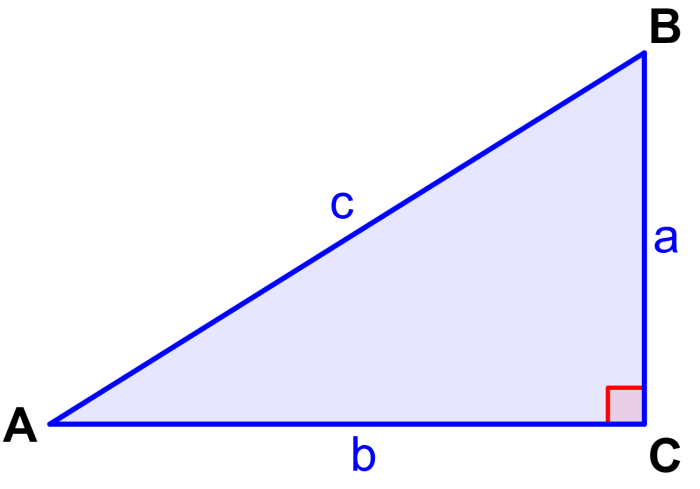
Similar a como el seno y el coseno pueden ser encontrados en términos de los lados de un triángulo rectángulo, también podemos hacer lo mismo con las tangentes. Vamos a usar al triángulo rectángulo ABC que tiene un ángulo recto en C.
Podemos usar las relaciones que ya hemos visto. Primero, tenemos $latex \tan(A)=\frac{\sin(A)}{\cos(A)}$. También usamos las relaciones $latex \sin(A)=\frac{a}{c}$ y $latex \cos(A)=\frac{b}{c}$.
Usando esto, podemos dividir a $latex \frac{a}{c}$ por $latex \frac{b}{c}$. Al cancelar a c en el numerado y el denominador, concluimos que $latex \tan(A)=\frac{a}{b}$. Esto significa que la tangente es igual al lado opuesto dividido por el lado adyacente:
| $latex \tan(x)=\frac{\text{opuesto}}{\text{adyacente}}$ |
Tangentes para ángulos especiales comunes
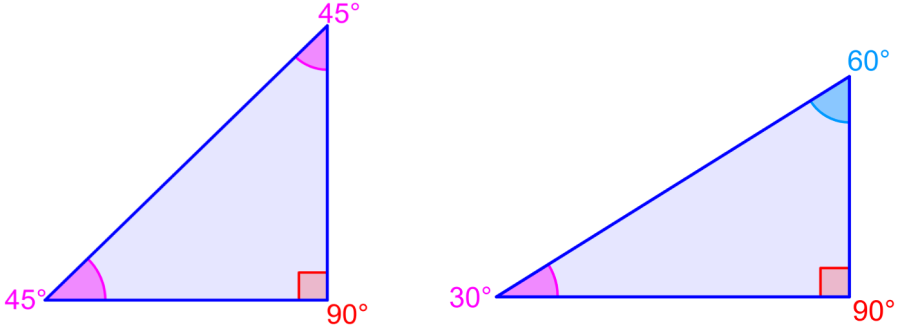
La tangente de los ángulos más comunes es encontrada usando las proporciones de los lados de triángulos especiales y el hecho que la tangente es igual al seno sobre el coseno. Por ejemplo, vamos a usar un triángulo isósceles rectángulo, el cual tiene los ángulos 45°-45°-90°.
Podemos usar el teorema de Pitágoras: $latex {{c}^2}={{a}^2}+{{b}^2}$. En este caso, dos lados son iguales, es decir, $latex a=b$. Entonces, tenemos $latex {{c}^2}=2{{a}^2}$. Esto significa que tenemos $latex c=a\sqrt{2}$.
Por lo tanto, tanto el seno como el coseno de 45° son iguales a $latex \frac{1}{\sqrt{2}}$ o $latex \frac{\sqrt{2}}{2}$. Dado que la tangente es igual al seno sobre el coseno, la tangente de 45° es igual a 1.
También usamos al triángulo especial 30°-60°-90°. Este triángulo tiene lados de proporción 1:$latex \sqrt{3}$:2. Usando estas proporciones, tenemos $latex \sin(30^{\circ})=\cos(60^{\circ})=\frac{1}{2}$ y también tenemos $latex \sin(60^{\circ})=\cos(30^{\circ})=\frac{\sqrt{3}}{2}$.
| Grados | Radianes | Seno | Coseno | Tangente |
| 90° | $latex \frac{\pi}{2}$ | 1 | 0 | Indefinido |
| 60° | $latex \frac{\pi}{3}$ | $latex \frac{\sqrt{3}}{2}$ | $latex \frac{1}{2}$ | $latex \sqrt{3}$ |
| 45° | $latex \frac{\pi}{4}$ | $latex \frac{\sqrt{2}}{2}$ | $latex \frac{\sqrt{2}}{2}$ | 1 |
| 30° | $latex \frac{\pi}{6}$ | $latex \frac{1}{2}$ | $latex \frac{\sqrt{3}}{2}$ | $latex \frac{\sqrt{3}}{3}$ |
| 0° | 0 | 0 | 1 | 0 |
Ejercicios de tangente de un ángulo resueltos
Los siguientes ejercicios son resueltos usando lo aprendido sobre las tangentes de ángulos. Todos los ejercicios hacen referencia al triángulo rectángulo visto arriba.
EJERCICIO 1
En un triángulo, tenemos $latex \tan(A)=1.2$ y $latex b=5$, ¿cuál es el valor de a?
Solución
Usamos el triángulo de arriba como referencia. Entonces, tenemos la relación $latex \tan(A)=\frac{b}{a}$. Usando los valores dados en esta fórmula y resolviendo para c, tenemos:
$latex \tan(A)=\frac{b}{a}$
$latex 1.2=\frac{5}{a}$
$latex a=\frac{5}{1.2}$
$latex a=4.17$
La longitud de a es 4.17.
EJERCICIO 2
Determina el valor de b si es que tenemos $latex a=11$ y $latex \tan(B)=0.78$.
Solución
Usamos el triángulo de arriba como referencia y podemos obtener la relación $latex \tan(B)=\frac{b}{a}$. Reemplazamos a los valores dados en esta fórmula y al resolver para c, tenemos:
$latex \tan(B)=\frac{b}{a}$
$latex 0.78=\frac{b}{11}$
$latex b=0.78(11)$
$latex b=8.58$
La longitud de b es 8.58.
EJERCICIO 3
Determina la medida del ángulo A si es que tenemos $latex a=12$ y $latex b=8$.
Solución
Formamos la expresión $latex \tan(A)=\frac{a}{b}$. Entonces, usando los valores dados, tenemos:
$latex \tan(A)=\frac{a}{b}$
$latex \tan(A)=\frac{12}{8}$
$latex \tan(A)=1.5$
Ahora, tenemos que usar la función $latex {{\tan}^{-1}}$ en una calculadora para obtener el resultado:
$latex {{\tan(1.5)}^{-1}}=56.3$°
El ángulo A mide 56.3°.
→ Calculadora de Tangente (Grados y Radianes)
Ejercicios de tangente de un ángulo para resolver
Usa la fórmula de la tangente vista arriba para resolver los siguientes ejercicios de práctica. Determina la longitud de un lado o la medida de un ángulo con la información dada.
Véase también
¿Interesado en aprender más sobre tangentes? Mira estas páginas: