El círculo unitario es utilizado en matemáticas para relacionar a las funciones trigonométricas básicas en una manera más fácil. Dado que el radio del círculo unitario es 1, esto facilita la aplicación del teorema de Pitágoras y resulta en que las coordenadas en x sean equivalentes al coseno y las coordenadas en y sean equivalentes al seno.
A continuación, aprenderemos más detalles sobre el círculo unitario usando diagramas. Conoceremos los valores de las funciones seno y coseno de los ángulos más importantes en términos de radianes.
¿Qué es el círculo unitario?
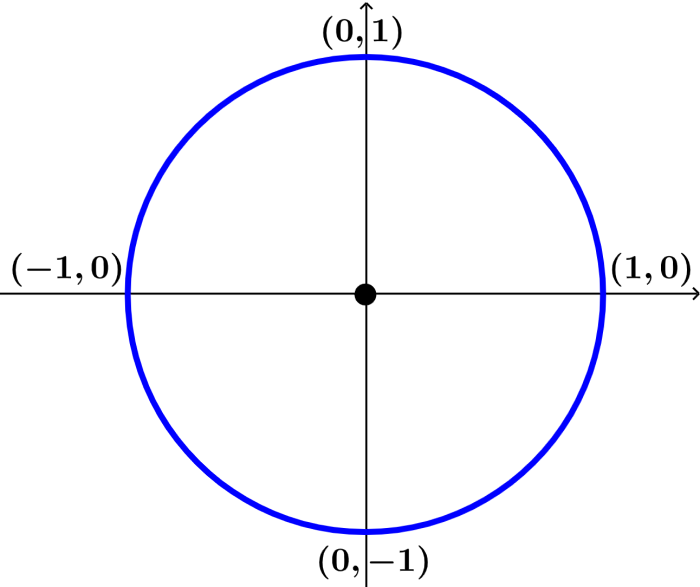
Un círculo unitario es un círculo que tiene un radio de 1. Por ejemplo, la siguiente imagen muestra un círculo unitario.
El círculo unitario es empleado en matemáticas para entender las relaciones de las diferentes funciones trigonométricas en el plano cartesiano. En este círculo, los valores del seno de un ángulo son equivalentes a las coordenadas en y y los valores del coseno de un ángulo son equivalentes a las coordenadas en x.
Usando el teorema de Pitágoras en el círculo unitario, podemos relacionar a las funciones trigonométricas seno, coseno y tangente.
Fórmula para el círculo unitario
La ecuación de un círculo está dada por la forma general:
$latex {{(x-h)}^2}+{{(y-k)}^2}={{r}^2}$
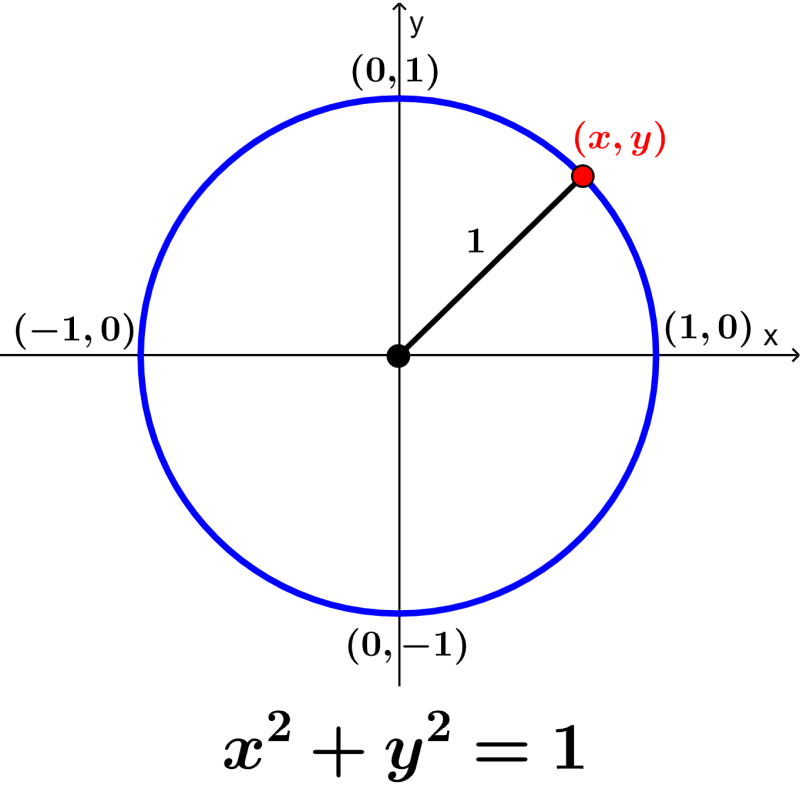
en donde, $latex (h, k)$ son las coordenadas del centro del círculo y r es el radio. Entonces, $latex (x, y)$ representan a los puntos en el círculo que se ubican a una distancia r desde el centro.
En el caso del círculo unitario, el centro está ubicado en (0, 0) y el radio es 1. Esto significa que la fórmula del círculo unitario es:
$latex {{x}^2}+{{y}^2}=1$
Calcular funciones trigonométricas usando el círculo unitario
Podemos calcular las funciones trigonométricas usando el círculo unitario. Para esto, tenemos que aplicar el teorema de Pitágoras en un círculo unitario para relacionar a las funciones trigonométricas.
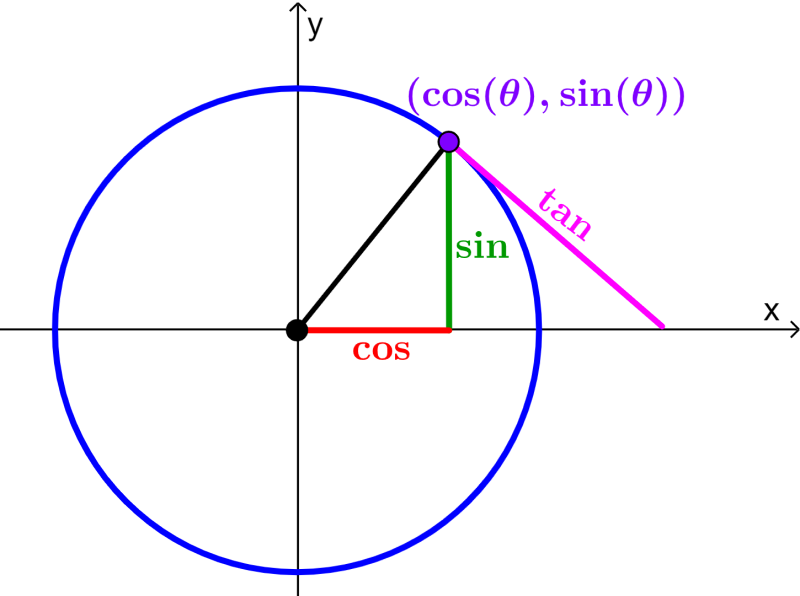
En el siguiente diagrama, tenemos graficadas a las funciones trigonométricas en un círculo unitario en el plano cartesiano.
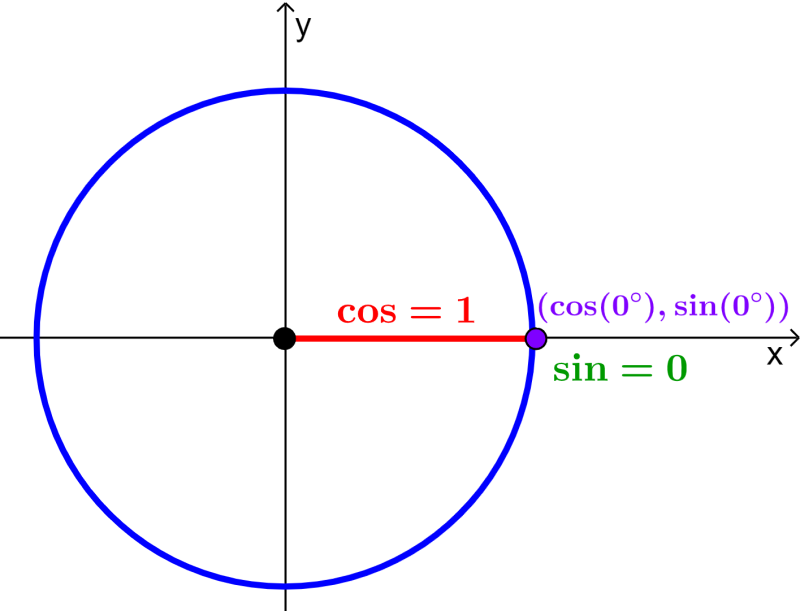
En el círculo unitario, el coseno es equivalente a la coordenada en x y el seno es equivalente a la coordenada en y. Por ejemplo, veamos lo que sucede cuando $latex \theta=0$.
Observamos que la coordenada en x es 1 y la coordenada en y es 0, por lo que tenemos:
- $latex \cos(0)=1$
- $latex \sin(0)=0$
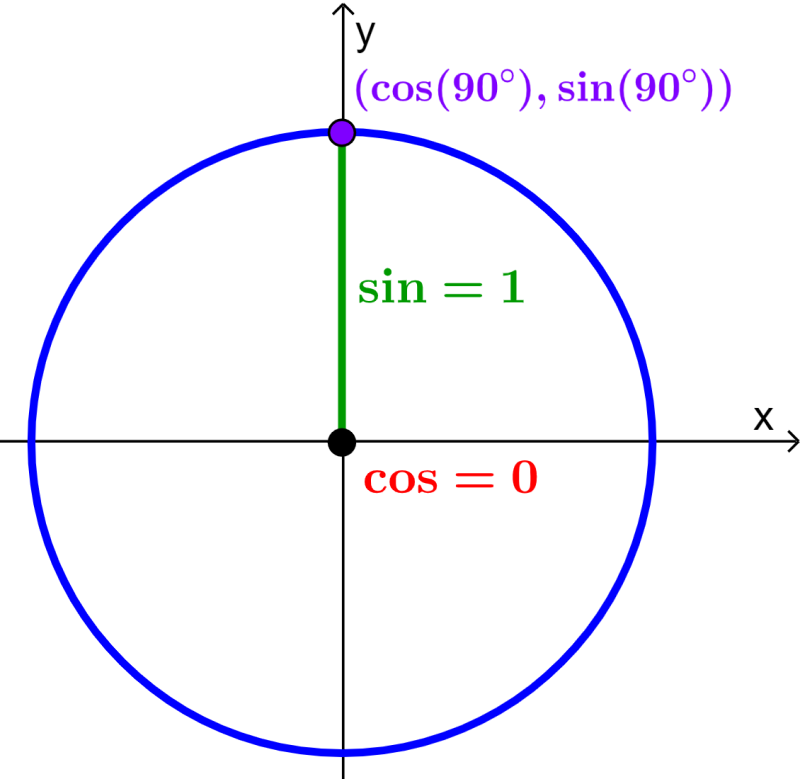
Ahora, veamos lo que sucede cuando $latex \theta=90$°.
En este caso, observamos que la coordenada en x es 0 y la coordenada en y es 1, por lo que tenemos:
- $latex \cos(90)=0$
- $latex \sin(90)=1$
Esto puede ser extendido a varios ángulos al considerar las proporciones de la coordenada x y de la coordenada y.
Círculo unitario en radianes
Muchas veces, medir a los ángulos en radianes resulta más útil, sobre todo en temas relacionados a Cálculo. Por esta razón, vamos a encontrar varios valores en el círculo unitario usando radianes. Recordemos que una vuelta completa al círculo unitario es igual a 360°, lo cual es igual a 2π radianes.
Podemos convertir a los ángulos en radianes y expresar en términos de radianes:
| Ángulo | Radianes | Seno | Coseno |
| 0° | 0 | 0 | 1 |
| 30° | $latex \frac{\pi}{6}$ | $latex \frac{1}{2}$ | $latex \frac{\sqrt{3}}{2}$ |
| 45° | $latex \frac{\pi}{4}$ | $latex \frac{\sqrt{2}}{2}$ | $latex \frac{\sqrt{2}}{2}$ |
| 60° | $latex \frac{\pi}{3}$ | $latex \frac{\sqrt{3}}{2}$ | $latex \frac{1}{2}$ |
| 90° | $latex \frac{\pi}{2}$ | 1 | 0 |
Estos son los valores de las funciones trigonométricas en el primer cuadrante del círculo unitario. Los números $latex \frac{1}{2}$, $latex \frac{\sqrt{2}}{2}$, $latex \frac{\sqrt{3}}{2}$, 0 y 1 se repiten tomando en cuenta los signos de los 4 cuadrantes:
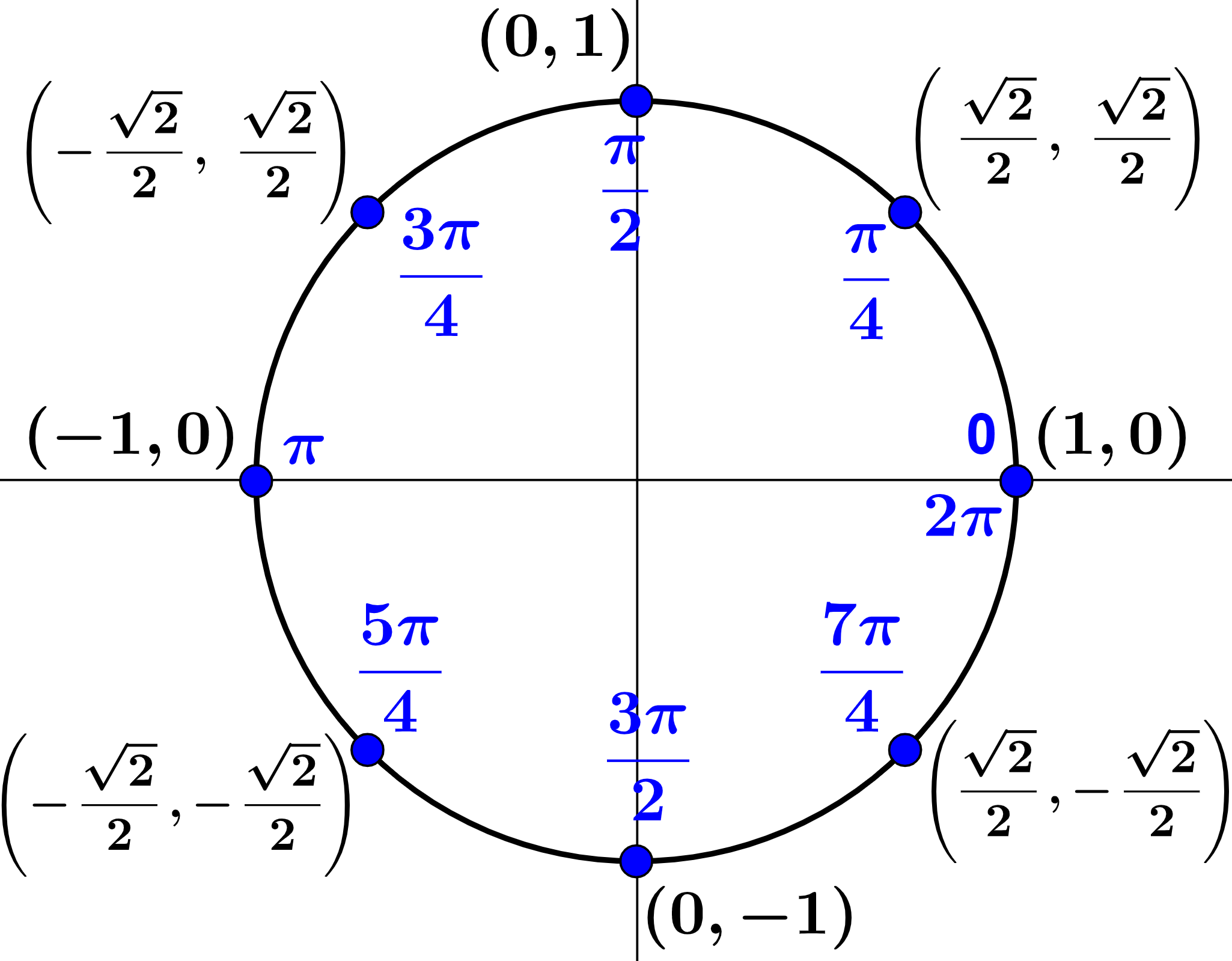
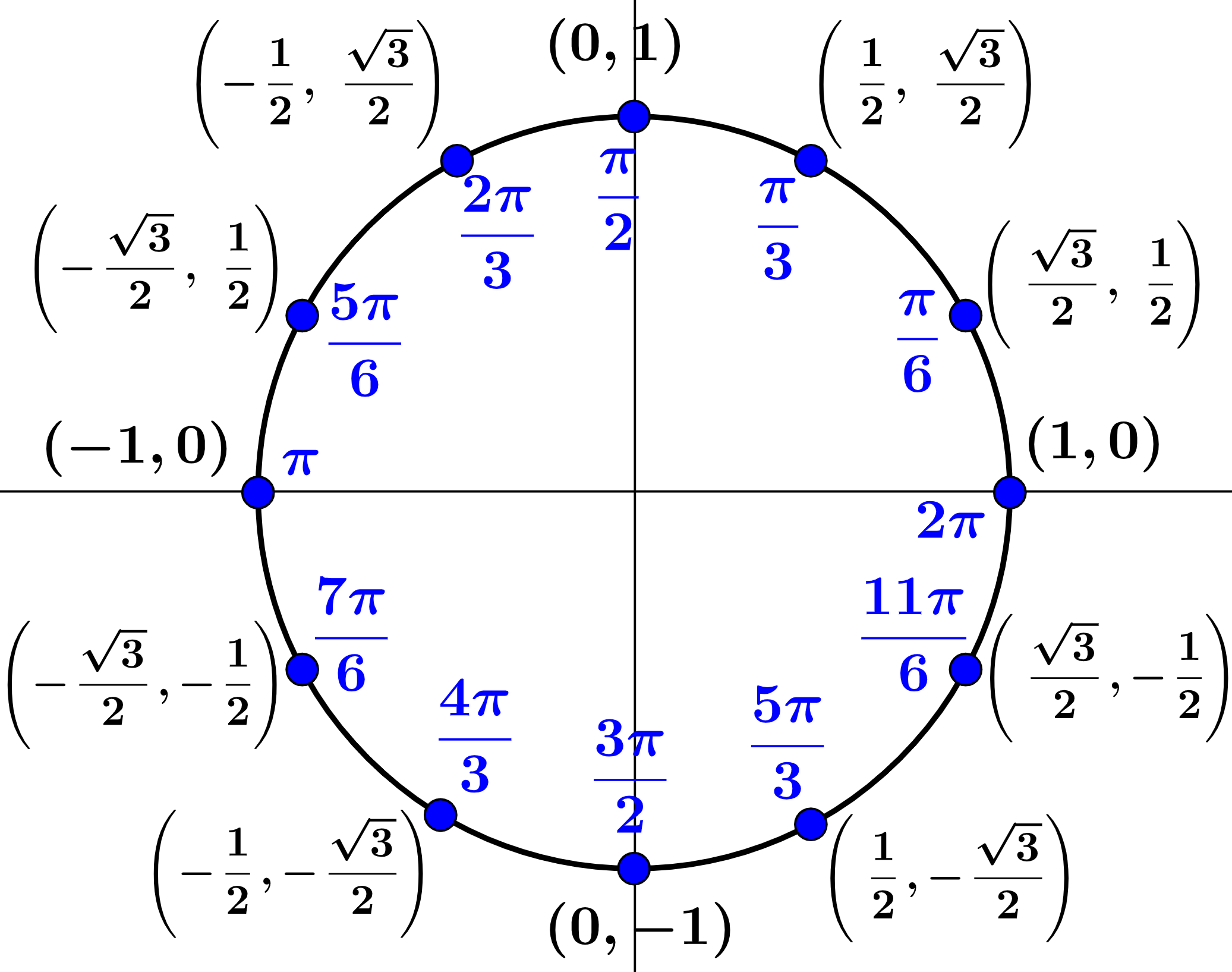
Entonces, los siguientes diagramas representan al círculo unitario con los valores de las funciones trigonométricas de los ángulos más importantes.
Véase también
¿Interesado en aprender más sobre tangentes? Mira estas páginas: