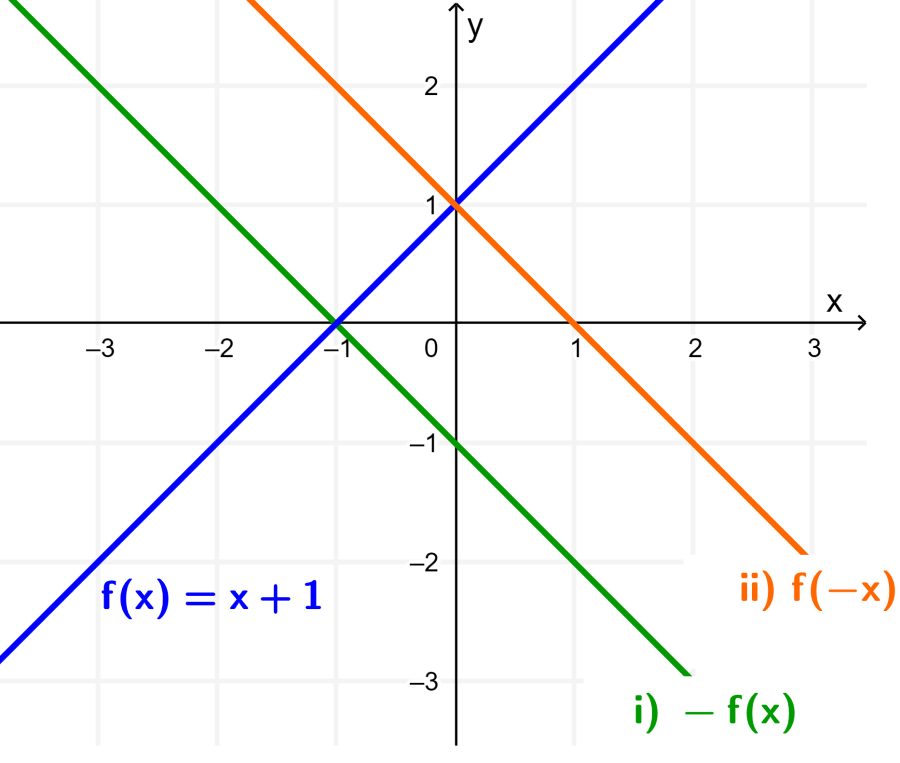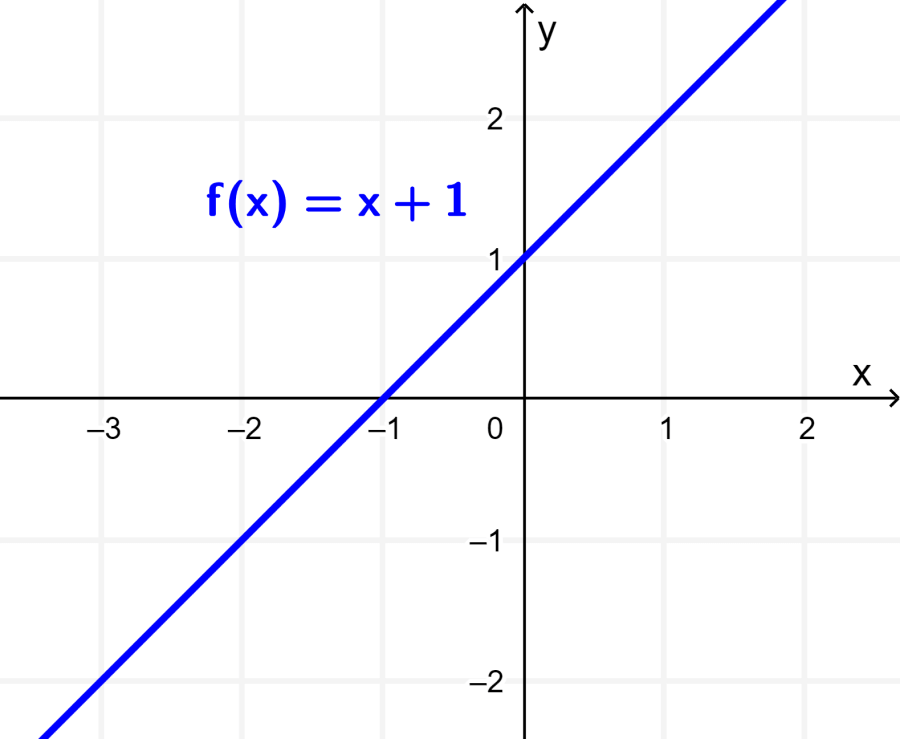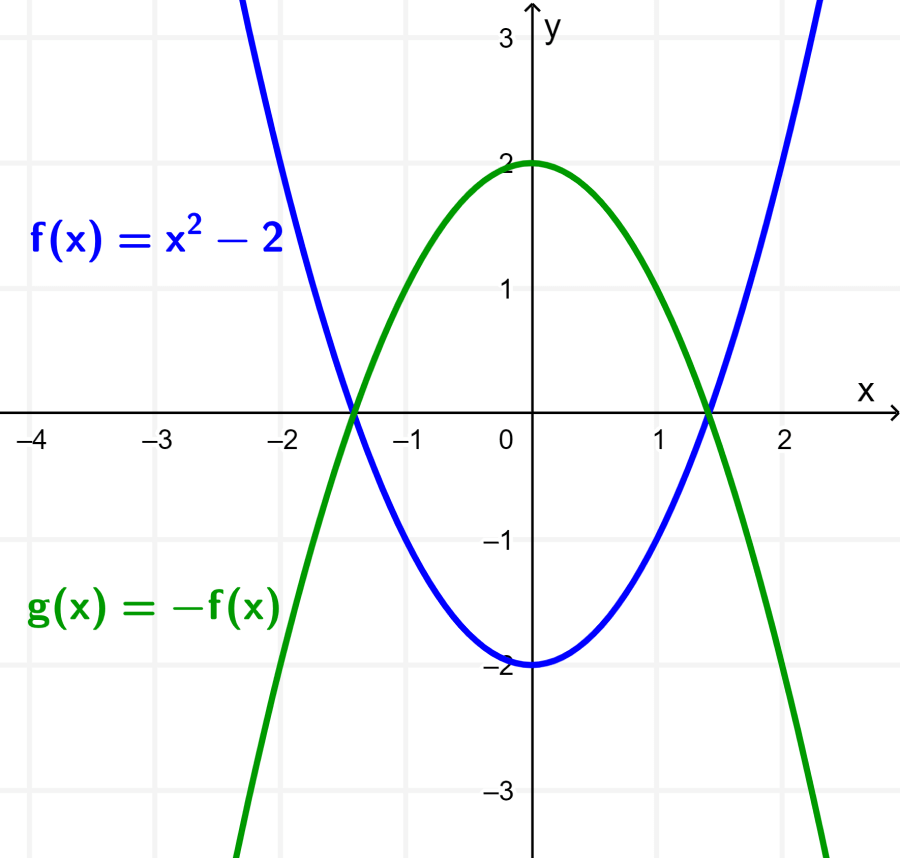La transformación de funciones son los cambios que podemos aplicar en una función para modificar su gráfica. Una de las transformaciones importantes es la reflexión de funciones. Una función puede ser reflejada con respecto al eje x cuando tenemos –f(x) y puede ser reflejada con respecto al eje y cuando tenemos f(-x).
A continuación, aprenderemos cómo obtener una reflexión de una función, tanto en el eje x como en el eje y. Usaremos ejemplos para ilustrar las ideas importantes.
ÁLGEBRA
Relevante para…
Aprender a sobre la reflexión de funciones en el eje x y el eje y.
ÁLGEBRA
Relevante para…
Aprender a sobre la reflexión de funciones en el eje x y el eje y.
Realizar reflexiones de una función con respecto al eje x y al eje y
Las reflexiones de una función son transformaciones que logran que la gráfica de la función sea reflejada con respecto a uno de los ejes. Una reflexión es equivalente a «darle la vuelta» a la gráfica de la función usando los ejes como referencia.
Podemos entender este concepto usando a la función $latex f(x)=x+1$. Cuando graficamos esta función, obtenemos la recta mostrada en la siguiente gráfica:
Ahora, podemos realizar dos transformaciones diferentes en la función $latex f(x)$ para obtener las siguientes funciones:
(i) $latex -f(x)=-(x+1)=-x-1$
(ii) $latex f(-x)=(-x)+1=-x+1$
Si es que graficamos a las funciones (i) y (ii) junto con la función $latex f(x)$ original, tenemos:
En el caso (i), la gráfica de la función original $latex f(x)$ ha sido reflejada con respecto al eje x.
En el caso (ii), la gráfica de la función original $latex f(x)$ ha sido reflejada con respecto al eje y.
En resumen, tenemos:
- La transformación $latex -f(x)$, resulta en una reflexión de la gráfica de $latex f(x)$ con respecto al eje x.
- La transformación $latex f(-x)$, resulta en una reflexión de la gráfica de $latex f(x)$ con respecto al eje y.
Ejemplos de reflexión de funciones
En los siguientes ejemplos, aplicamos lo aprendido sobre la reflexión de funciones con respecto al eje x y con respecto al eje y. Cada ejemplo tiene una solución detallada.
EJEMPLO 1
Traza la gráfica de la función $latex f(x)=x^2-2$ y luego, grafica la función $latex g(x)=-f(x)$.
Solución
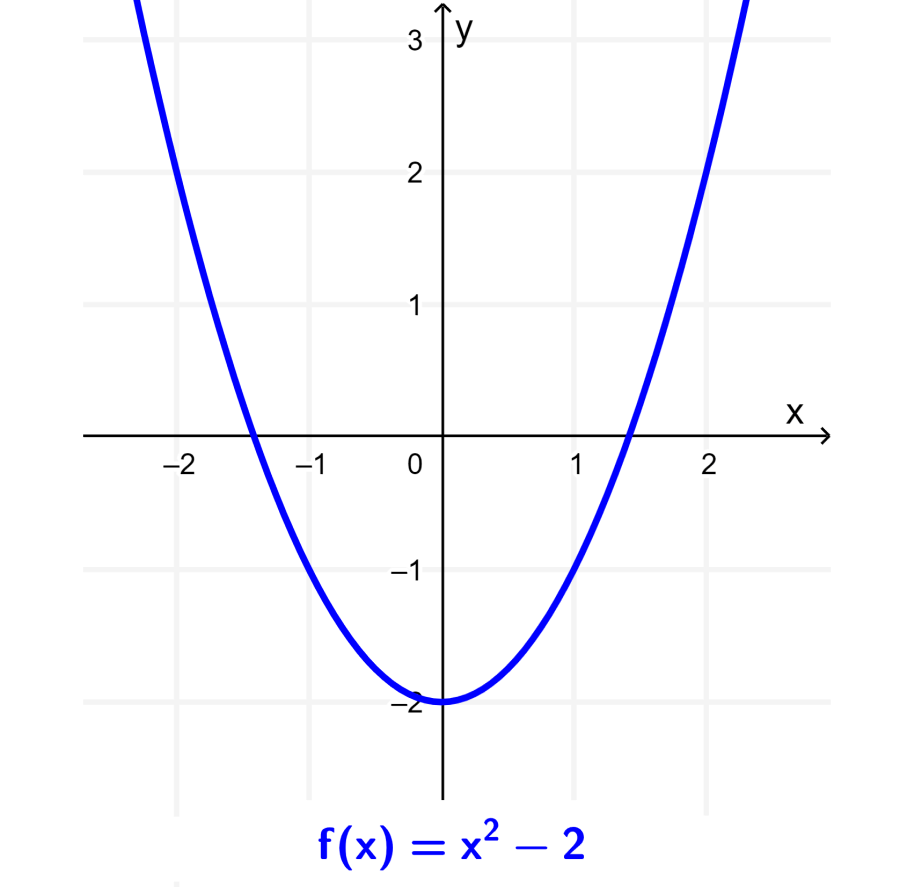
La gráfica de f es una parábola con un desplazamiento de 2 unidades hacia abajo, como se muestra en la siguiente gráfica:
Ahora, cuando aplicamos la transformación en la función g, obtenemos $latex g(x)=-x^2+2$. Podemos obtener su gráfica al al reflejar a la gráfica de f con respecto al eje x:
.
EJEMPLO 2
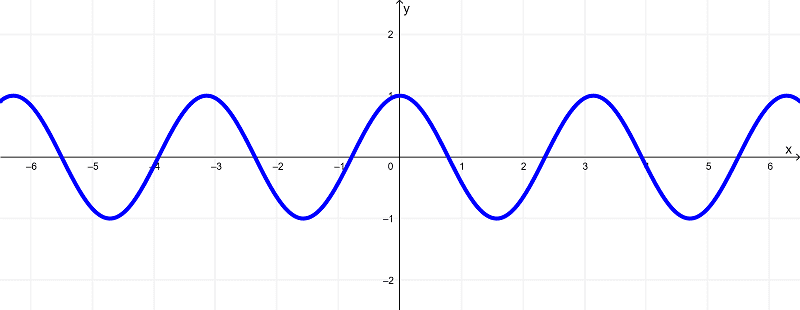
¿Cuál es la diferencia entre la gráfica de $latex f(x)=\cos(2x)$ y la gráfica de $latex g(x)=\cos(-2x)$?
Solución
La gráfica de la función $latex f(x)=\cos(2x)$ es la siguiente:
Podemos observar que la función g es equivalente a $latex g(x)=f(-x)$. Entonces, la función g es obtenida al aplicar una reflexión con respecto al eje y.
Ahora, podemos mirar que la gráfica de $latex f(x)=\cos(2x)$ tiene una simetría con respecto al eje y. Esto significa que si es que la reflejamos con respecto al eje y, obtendremos la misma gráfica.
Entonces, las gráficas de $latex f(x)=\cos(2x)$ y de $latex g(x)=\cos(-2x)$ son las mismas.
EJEMPLO 3
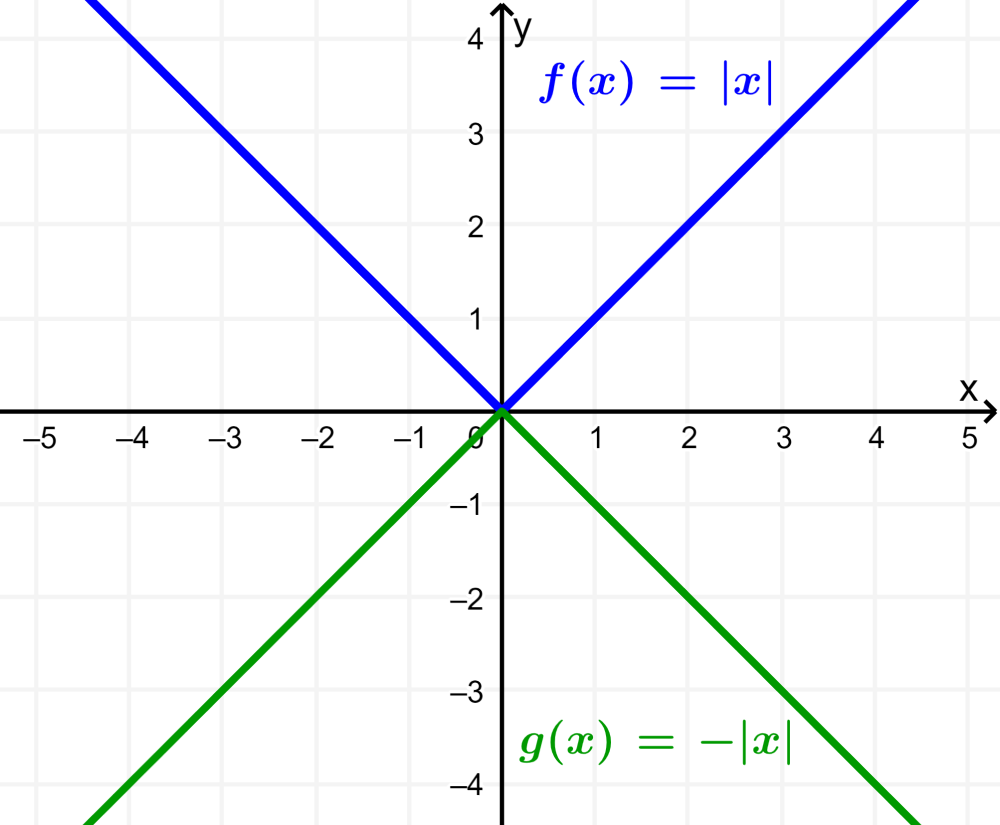
Grafica la función valor absoluto en su forma base y luego grafica a $latex g(x)=-|x|$.
Solución
La gráfica de la función valor absoluto en su forma base, $latex f(x)=|x|$, es la siguiente:
Ahora, podemos observar que la función g es igual a $latex g(x)=-f(x)$. Entonces, obtenemos la gráfica de g al aplicar una reflexión con respecto al eje x de la gráfica de f.
.
EJEMPLO 4
¿Cuál es una función que tiene una reflexión con respecto al eje y de la función $latex f(x)=3x^2+5x+3$?
Solución
Para obtener una reflexión con respecto al eje y, tenemos que aplicar la transformación $latex g(x)=f(-x)$.
Entonces, podemos encontrar la función g al sustituir –x por x en la función f:
$latex g(x)=3(-x)^2+5(-x)+3$
$latex g(x)=3x^2-5-x+3$
Ejercicios de reflexión de funciones para resolver
Resuelve los siguientes ejercicios usando todo lo aprendido sobre la reflexión de funciones.
Véase también
¿Interesado en aprender más sobre transformaciones de funciones? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
