Existen varias transformaciones que podemos aplicar a las funciones para modificar sus gráficas. Podemos realizar aplicar un desplazamiento vertical o un desplazamiento horizontal. Además, también podemos producir reflexiones con respecto al eje x y al eje y. Por último, podemos estirar o comprimir a las gráficas.
A continuación, conoceremos las diferentes transformaciones usadas para modificar las gráficas de las funciones. Usaremos varios ejemplos para entender las ideas.
Desplazamiento vertical de una función
Consideremos a la función f definida por $latex f(x)=x^2$. Si es que graficamos esta función, tenemos lo siguiente:
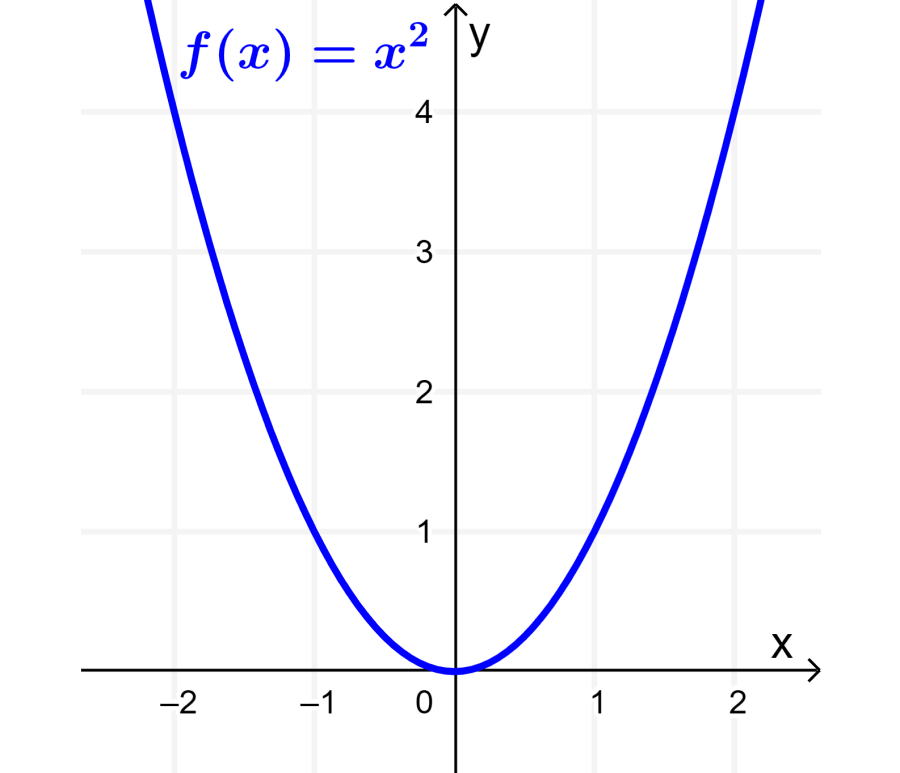
Ahora, si es que simplificamos las expresiones para (i) $latex f(x)+1$ y para (ii) $latex f(x)-1$, tenemos:
(i) $latex f(x)+1=x^2+1~$ y (ii) $latex f(x)-1=x^2-1$
Al graficar las funciones (i) y (ii) en el mismo plano cartesiano que la función original, obtenemos las curvas mostradas en el siguiente diagrama:
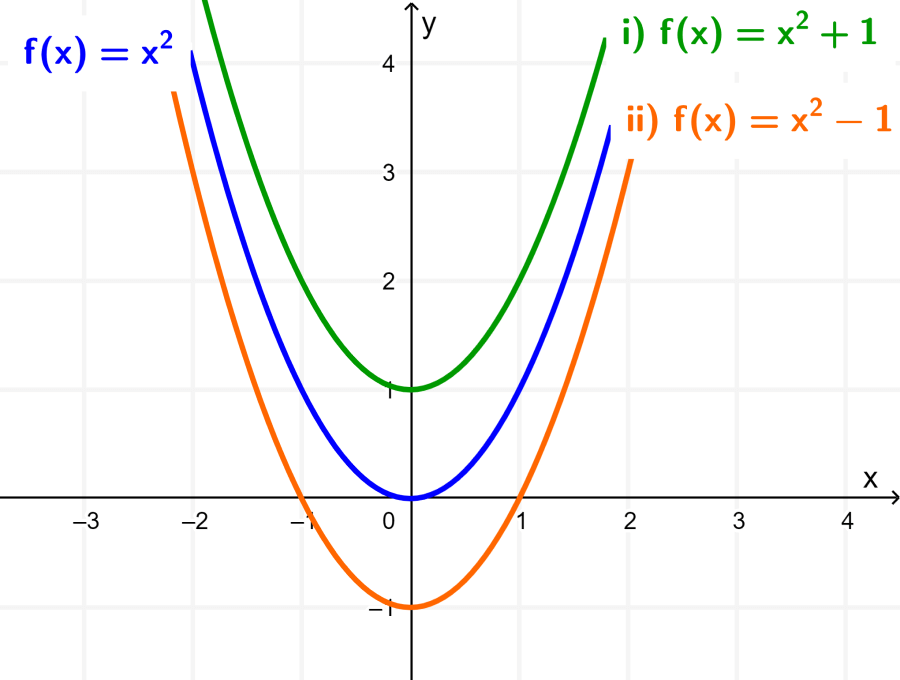
En el caso (i), la gráfica de f ha sido trasladada 1 unidad hacia arriba. Es decir, 1 unidad paralela al eje y.
En el caso (ii), la gráfica de f ha sido trasladada 1 unidad hacia abajo. Es decir, -1 unidad paralela al eje y.
En general, tenemos lo siguiente:
- La transformación $latex f(x)+a$, en donde $latex a$ es una constante, produce un desplazamiento en la gráfica de f de $latex a$ unidades paralelo al eje y (hacia arriba).
- La transformación $latex f(x)-a$, en donde $latex a$ es una constante, produce un desplazamiento en la gráfica de f de $latex -a$ unidades paralelo al eje y (hacia abajo).
EJEMPLO
La función f está definida por $latex f(x)=x^3$. Traza la gráfica de f y luego traza la gráfica de $latex g(x)=x^3-3$.
Solución: La gráfica de f está mostrada en la parte izquierda de la siguiente gráfica.
Dado que $latex g(x)=f(x)-3$, podemos obtener la gráfica de la función g al trasladar a la gráfica de f por -3 unidades con respecto al eje y (3 unidades hacia abajo). Esta gráfica es mostrada en la derecha:
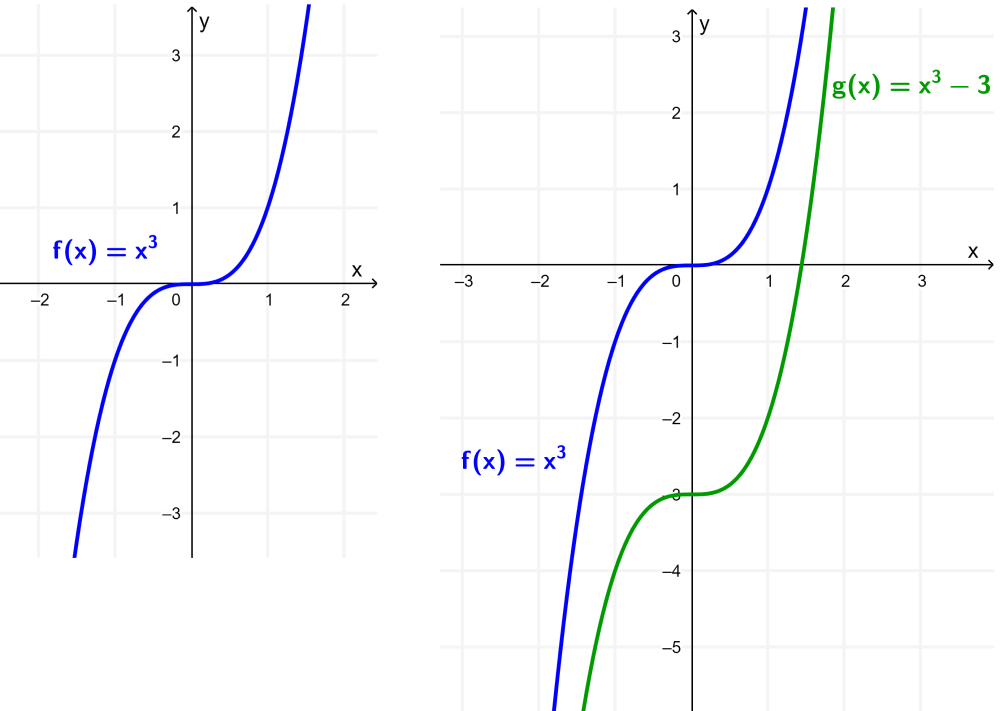
Desplazamiento horizontal de una función
Consideremos a la función f definida por $latex f(x)=2x-1$. Al graficar esta función, obtenemos una recta como se muestra en la siguiente gráfica:
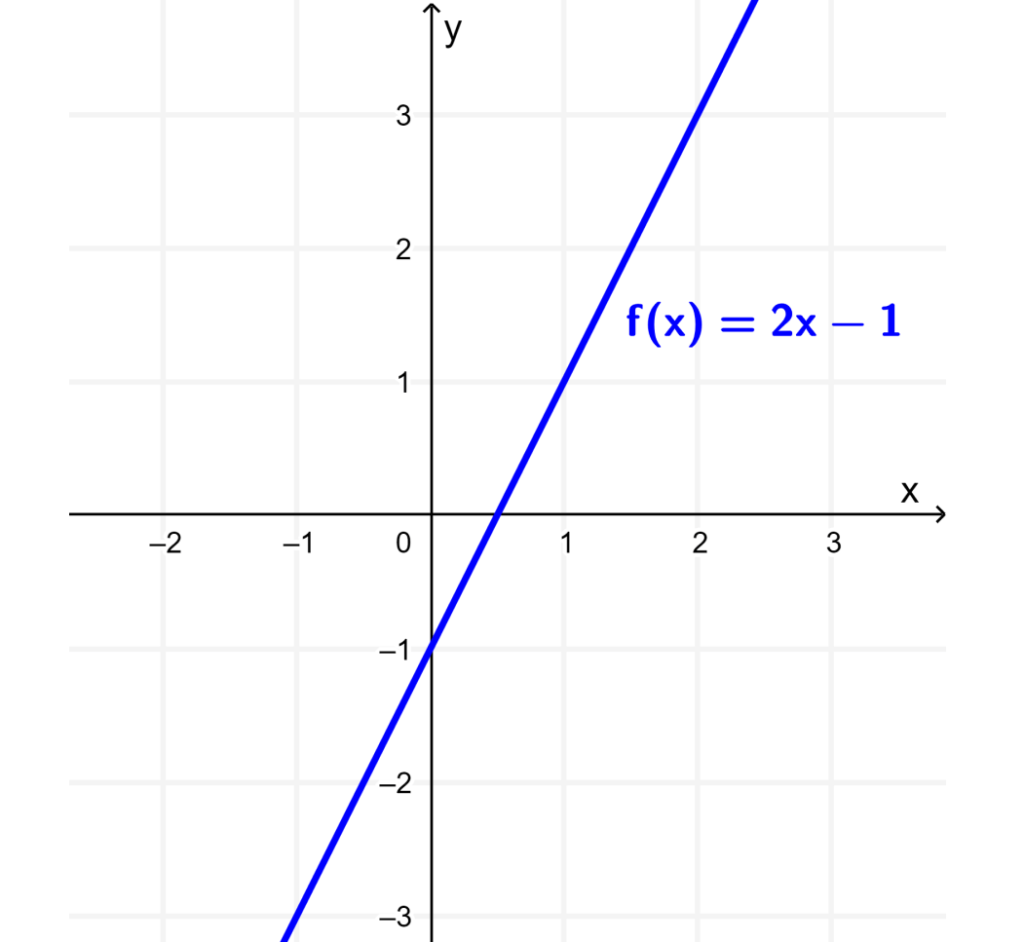
Ahora, si es que simplificamos las expresiones para (i) $latex f(x+2)$ y para (ii) $latex f(x-2)$, tenemos:
(i) $latex f(x+2)=2(x+2)-1~$ y (ii) $latex f(x-2)=2(x-2)-1$
(i) $latex f(x+2)=2x+3~$ y (ii) $latex f(x-2)=2x-5$
Si es que graficamos a las funciones (i) y (ii) en el mismo plano cartesiano que la función original, obtenemos las siguientes rectas:
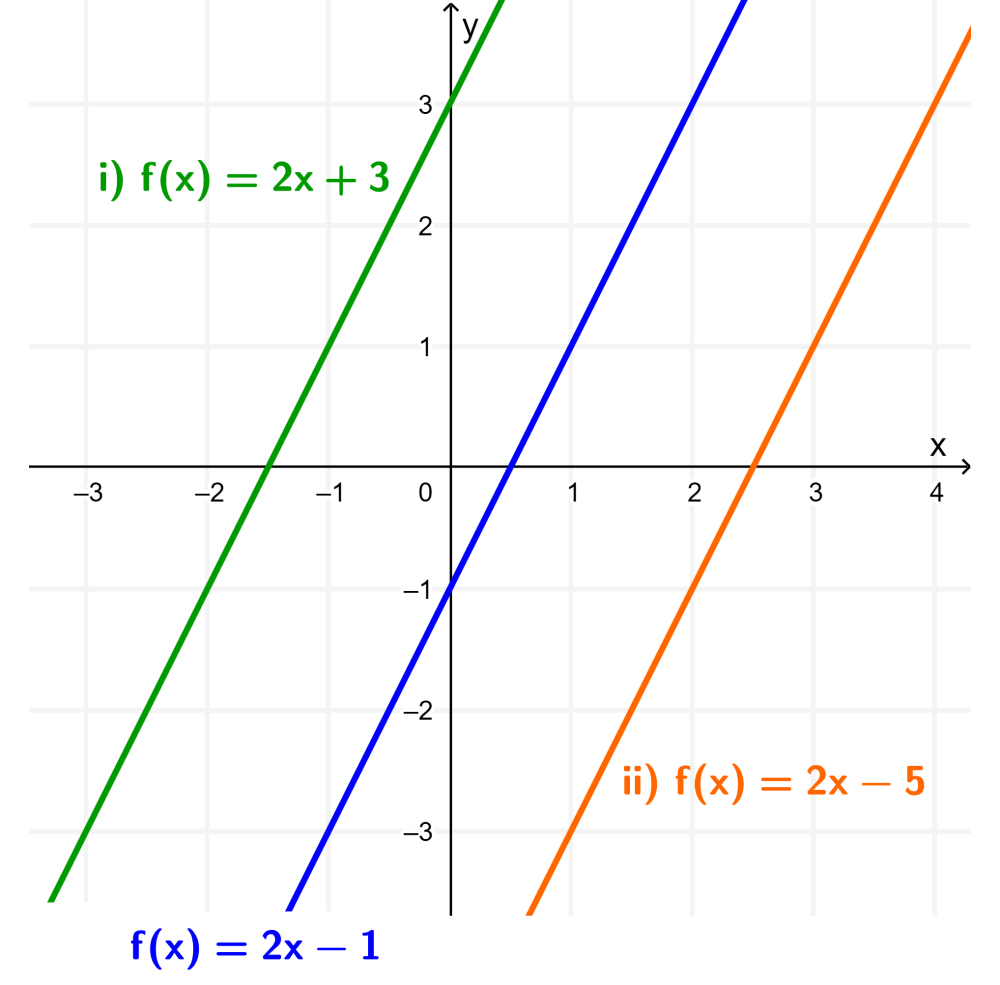
En el caso (i), la gráfica de f ha sido trasladada 2 unidades hacia la izquierda. Es decir, -2 unidades paralelas al eje x.
En el caso (ii), la gráfica de f ha sido trasladada 2 unidades hacia la derecha. Es decir, 2 unidades paralelas al eje x.
En general, tenemos lo siguiente:
- La transformación $latex f(x+a)$, en donde $latex a$ es una constante, produce un desplazamiento en la gráfica de f de $latex -a$ unidades paralelas al eje x (hacia la izquierda).
- La transformación $latex f(x-a)$, en donde $latex a$ es una constante, produce un desplazamiento en la gráfica de f de $latex a$ unidades paralelas al eje x (hacia la derecha).
EJEMPLO
Grafica la función $latex f(x)=x^2-1$. Luego, encuentra la versión simplificada de $latex g(x)=f(x+2)$ y grafícala.
Solución: La gráfica de la función f es la siguiente:
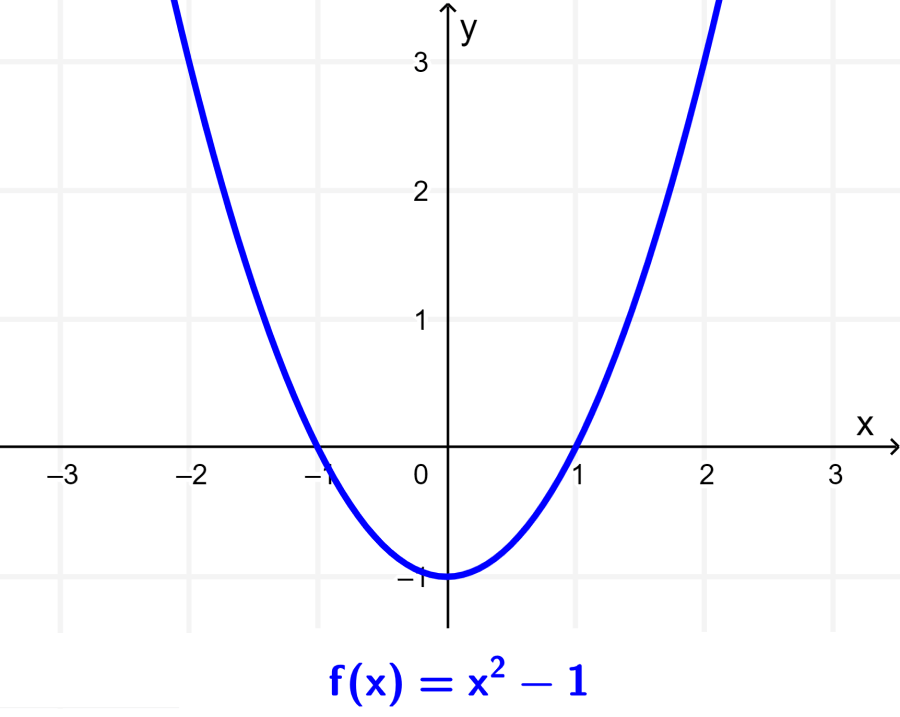
Ahora, la función g está dada por:
$latex g(x)=f(x+2)$
$latex =(x+2)^2-1$
$latex =x^2+4x+4-1$
$latex =x^2+4x+3$
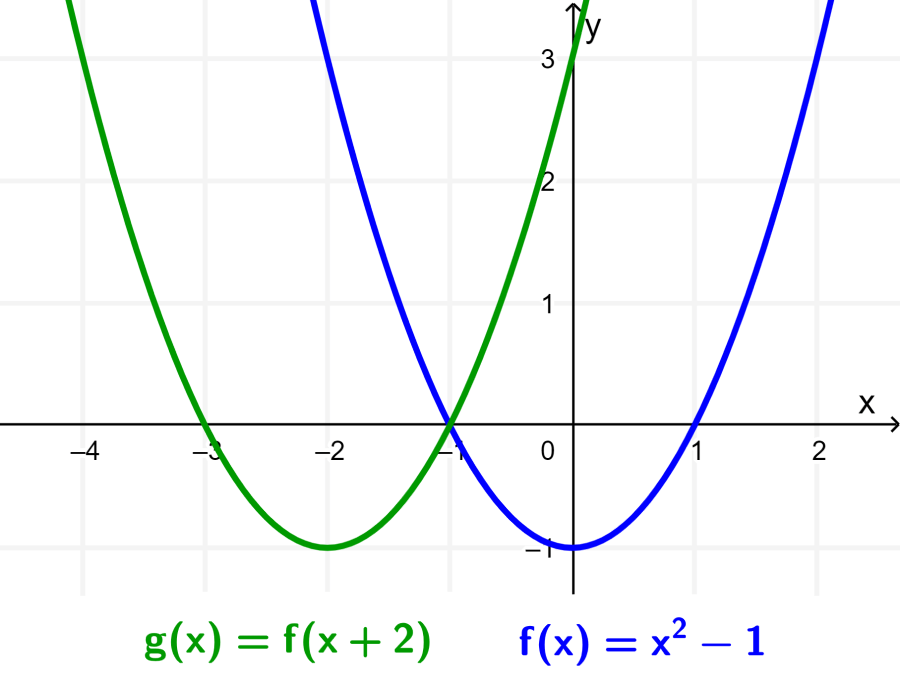
Dado que $latex g(x)=f(x+2)$, la gráfica de g puede ser obtenida al trasladar a la gráfica de f por 2 unidades hacia la izquierda, es decir, -2 unidades en el eje x.
Reflexión de funciones
Vamos a considerar a la función f definida por $latex f(x)=x+1$. Cuando graficamos esta función, obtenemos la recta mostrada en la siguiente gráfica:
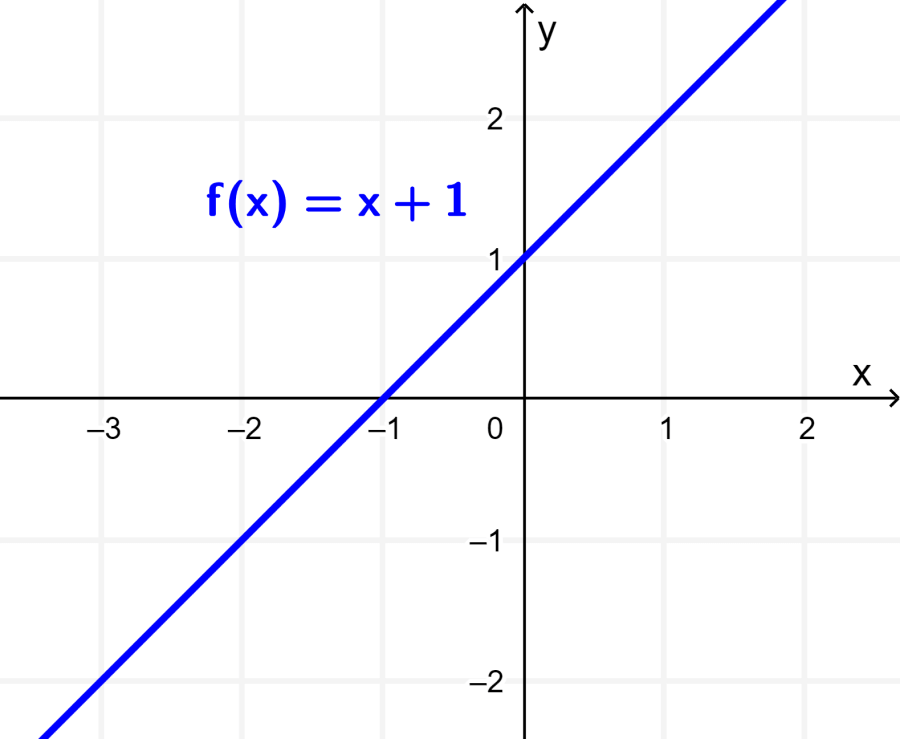
Ahora, vamos a considerar las siguientes funciones:
(i) $latex -f(x)=-(x+1)=-x-1$
(ii) $latex f(-x)=(-x)+1=-x+1$
Al graficar a las funciones (i) y (ii) en el mismo plano cartesiano que la función original, obtenemos las siguientes rectas:
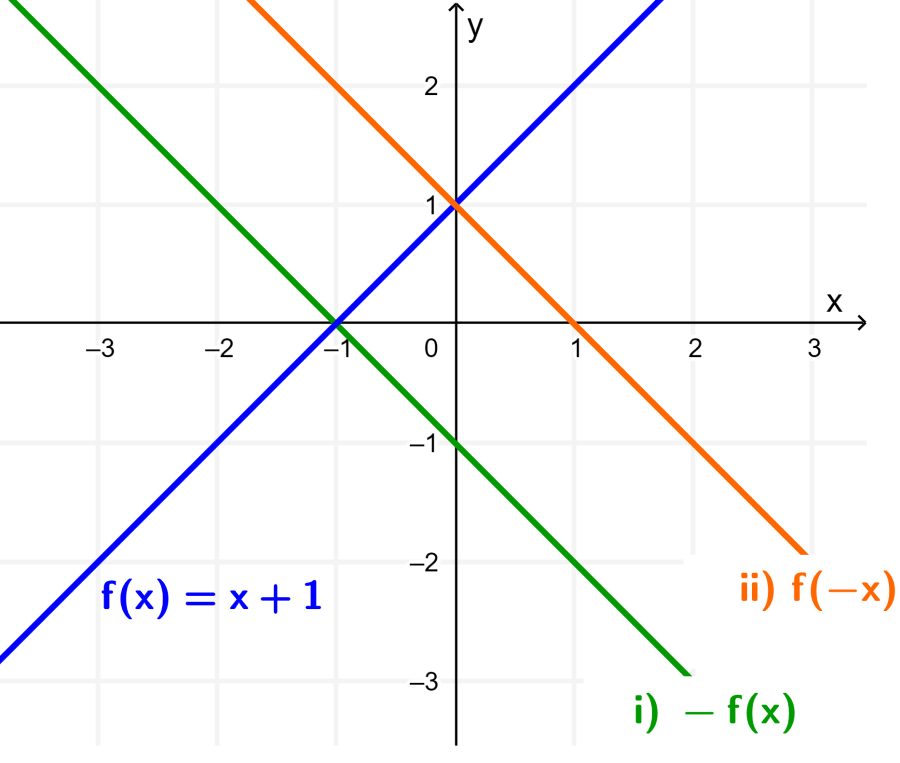
En el caso (i), la gráfica de f ha sido reflejada con respecto al eje x.
En el caso (ii), la gráfica de f ha sido reflejada con respecto al eje y.
En general, tenemos lo siguiente:
- La transformación $latex -f(x)$, produce una reflexión de la gráfica de f con respecto al eje x.
- La transformación $latex f(-x)$, produce una reflexión de la gráfica de f con respecto al eje y.
EJEMPLO
Grafica la función $latex f(x)=x^2-2$. Luego, grafica la función $latex g(x)=-f(x)$.
Solución: La gráfica de la función f es la siguiente:
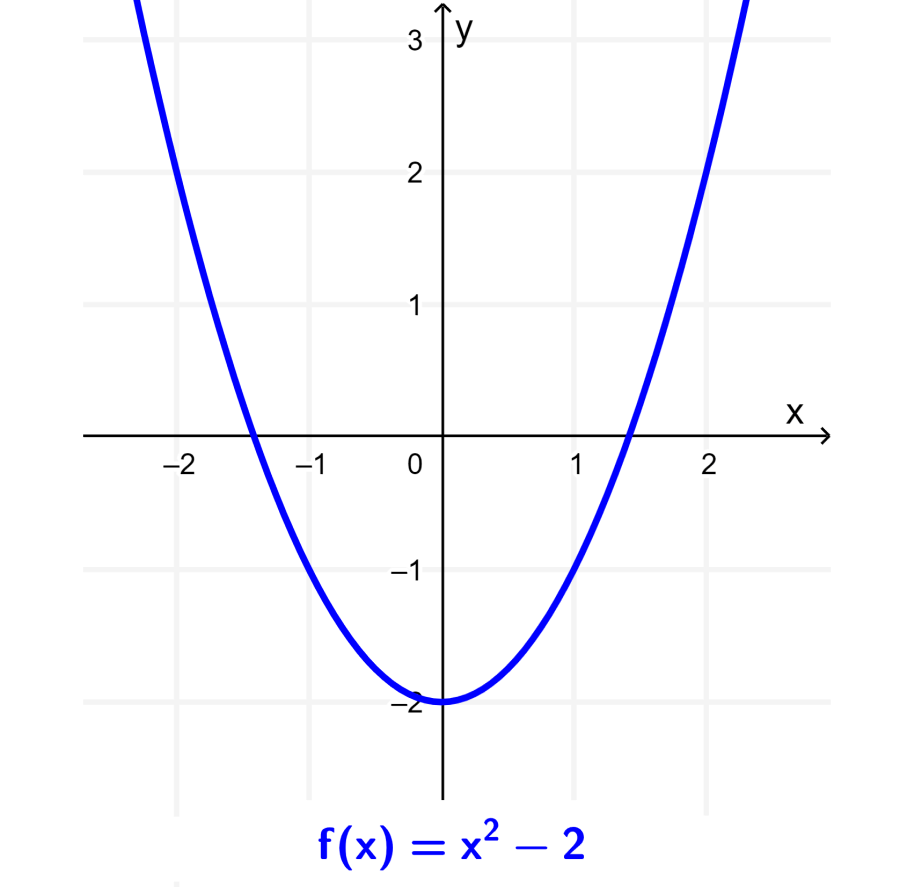
Ahora, la función g está dada por $latex g(x)=-x^2+2$ y su gráfica puede ser obtenida al reflejar a la gráfica de f con respecto al eje x:
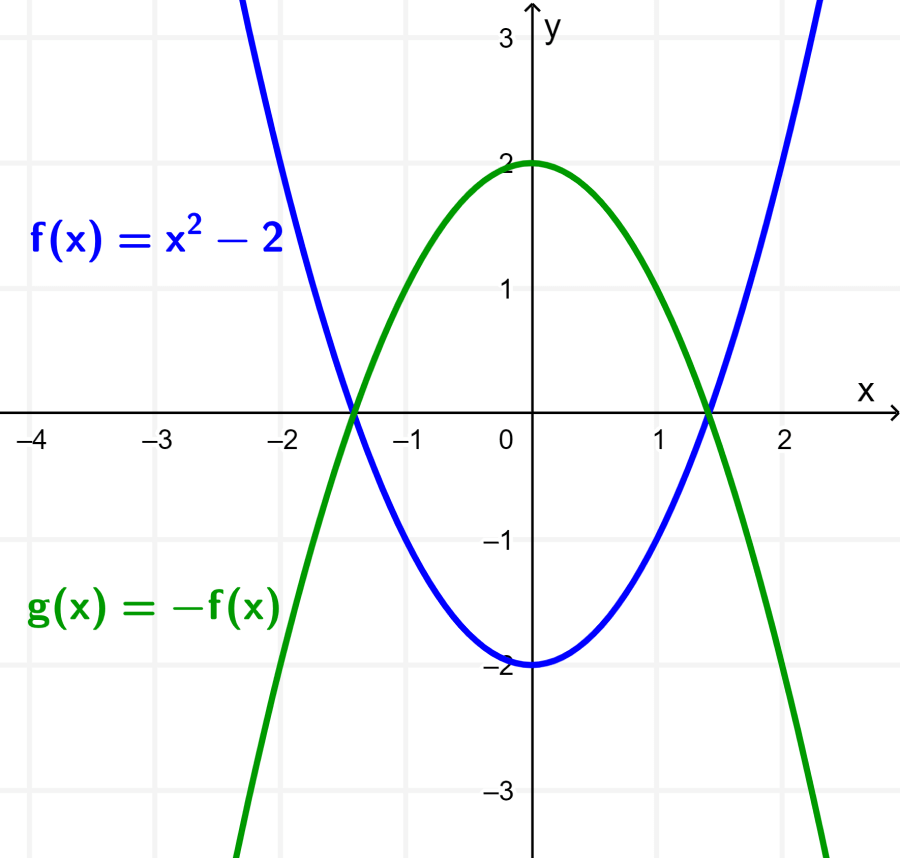
Estiramiento de funciones
Consideremos a la función f definida por $latex f(x)=x+1$. Cuando graficamos esta función, obtenemos la recta mostrada en la siguiente gráfica:
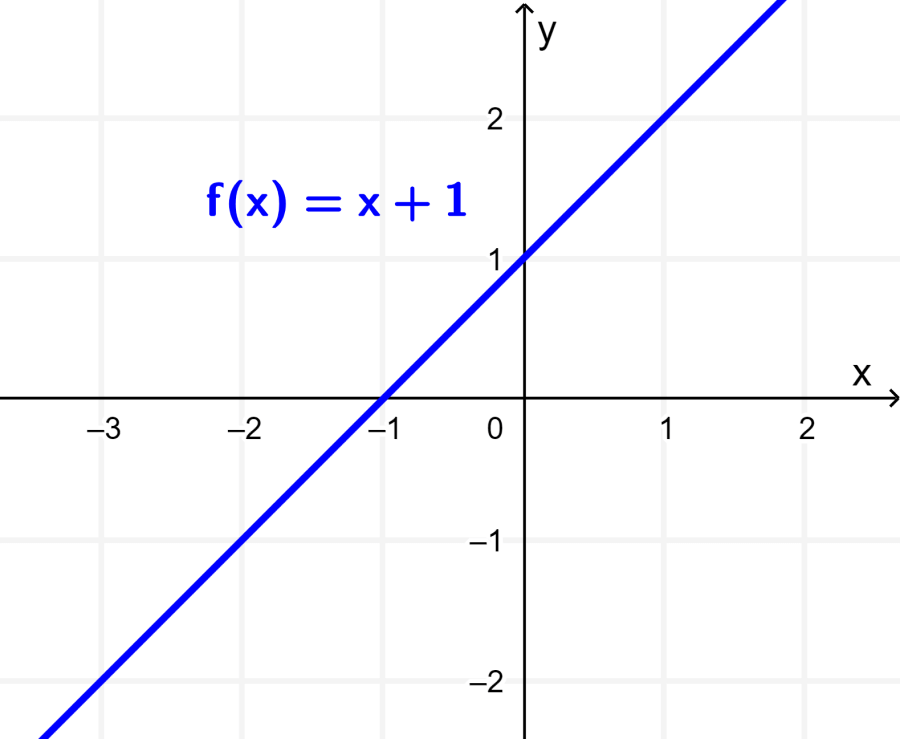
Ahora, vamos a considerar a las funciones (i) $latex f(2x)$ y (ii) $latex 2f(x)$. Entonces, tenemos:
(i) $latex f(2x)=(2x)+1~$ y (ii) $latex 2f(x)=2(x+1)$
(i) $latex f(2x)=2x+1~$ y (ii) $latex 2f(x)=2x+2$
Al graficar a las funciones (i) y (ii) en el mismo plano cartesiano que la función original, obtenemos lo siguiente:
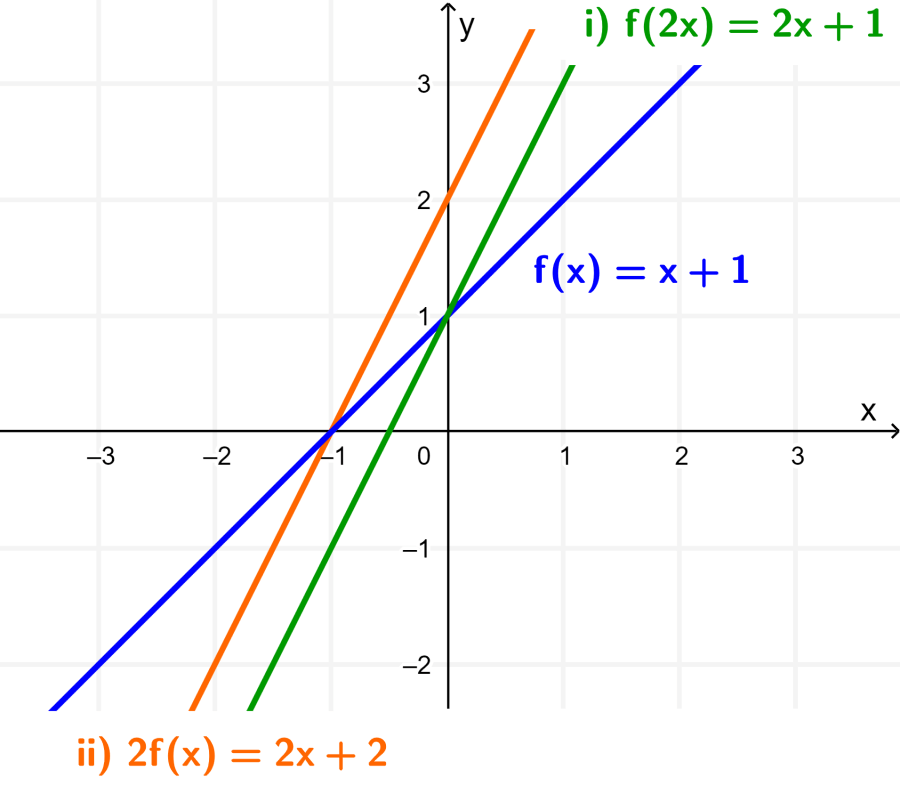
En el caso (i), la gráfica de f ha sido estirada con respecto al eje x por un factor de $latex \frac{1}{2}$.
En el caso (ii), la gráfica de f ha sido estirada con respecto al eje y por un factor de 2.
En general, tenemos lo siguiente:
- La transformación $latex f(ax)$, en donde $latex a$ es una constante, produce un estiramiento con respecto al eje x por un factor de $latex \frac{1}{a}$.
- La transformación $latex af(x)$, en donde $latex a$ es una constante, produce un estiramiento con respecto al eje y por un factor de $latex a$.
EJEMPLO
Grafica la función $latex f(x)=x+2$. Luego, grafica la función $latex g(x)=3f(x)$.
Solución: La gráfica de la función f es la siguiente:
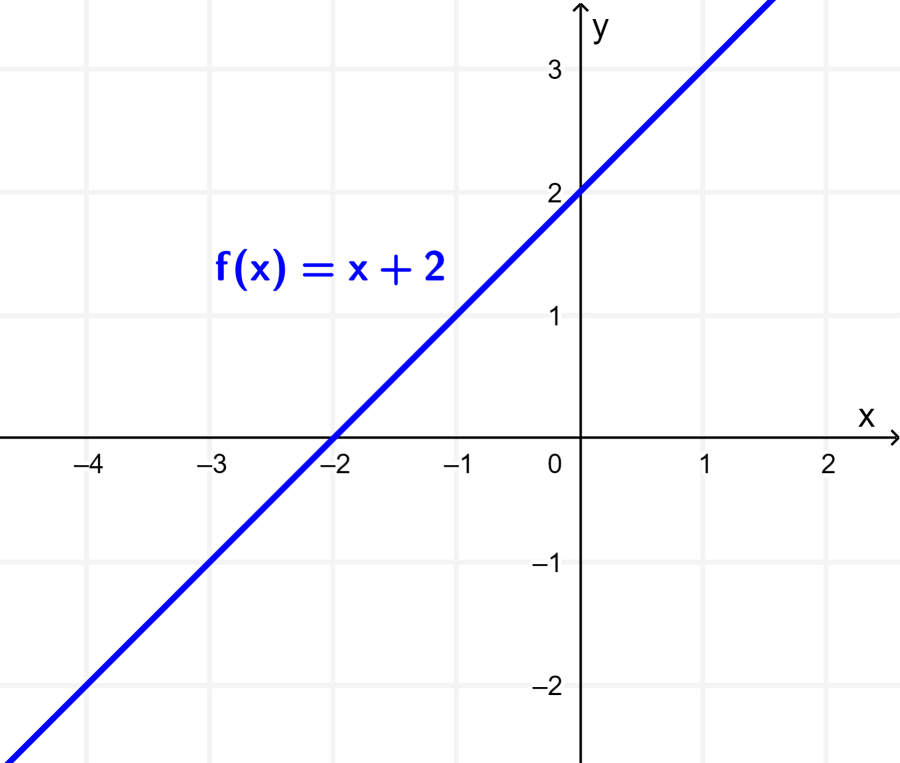
Cuando simplificamos, podemos observar que la función g está dada por $latex g(x)=3x+6$. Podemos obtener la gráfica de esta función al estirar la función de f por un factor de 3 con respecto al eje y.
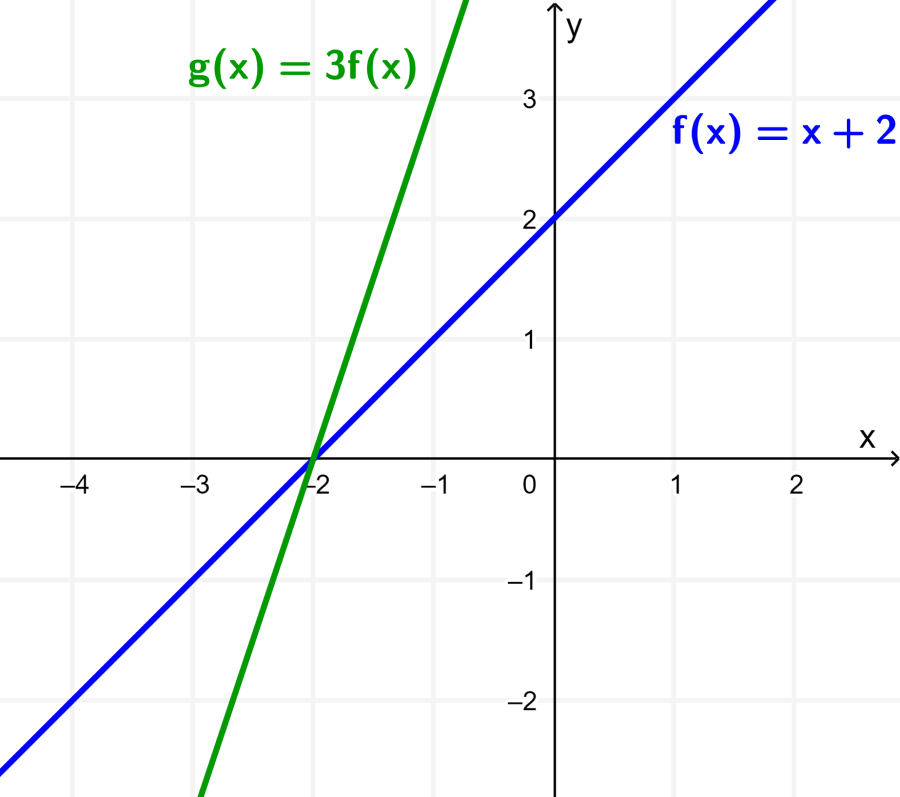
Véase también
¿Interesado en aprender más sobre transformaciones de funciones? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
