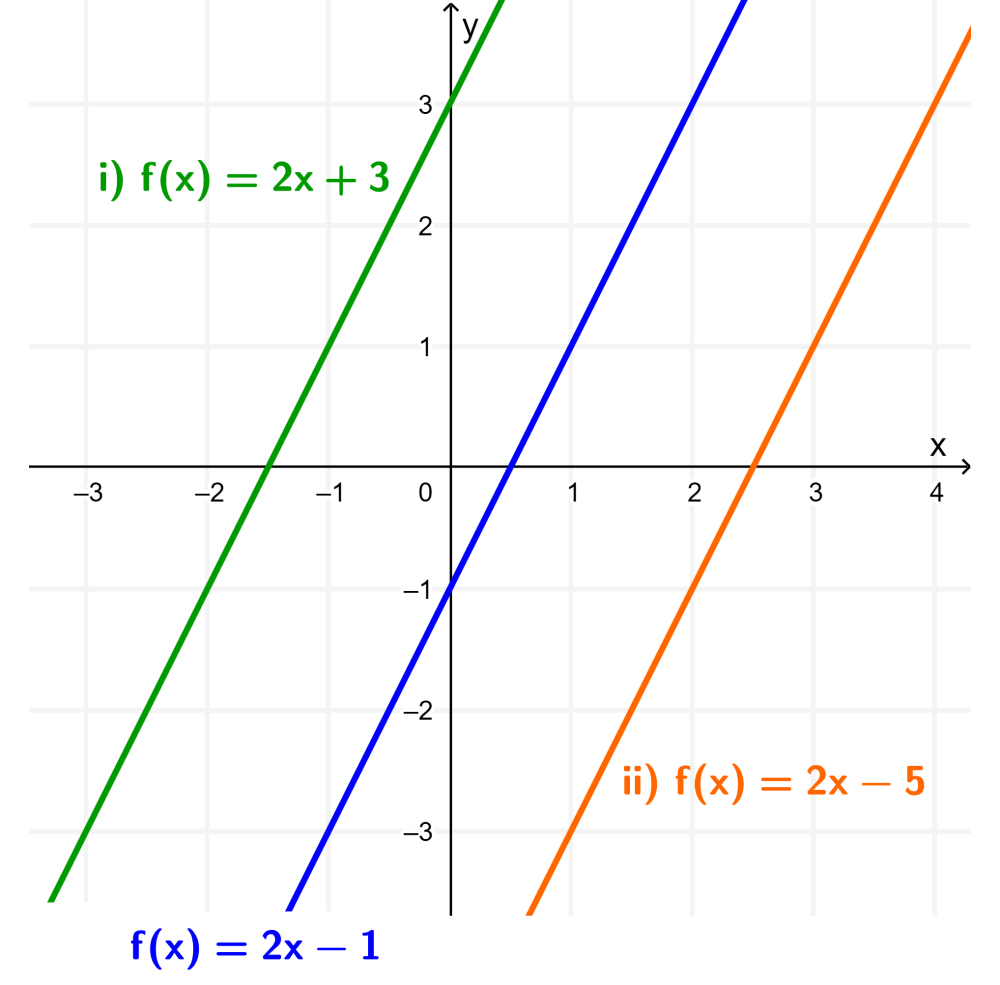El desplazamiento horizontal y vertical es una transformación que nos permiten modificar a la gráfica de la función original. Dada la función f(x), podemos trasladar a la función horizontalmente con la transformación f(x+a) y verticalmente con la transformación f+a en donde a es un valor que puede ser positivo o negativo.
A continuación, aprenderemos todo lo relacionado con el desplazamiento horizontal y vertical de una función. Veremos algunos ejemplos para ilustrar los conceptos.
ÁLGEBRA
Relevante para…
Aprender a sobre el desplazamiento horizontal y vertical de funciones.
ÁLGEBRA
Relevante para…
Aprender a sobre el desplazamiento horizontal y vertical de funciones.
Determinar el desplazamiento horizontal de una función
El desplazamiento horizontal en una función es una transformación que produce un movimiento hacia la izquierda o hacia la derecha en la función original. Es decir, el desplazamiento sucede paralelo al eje x.
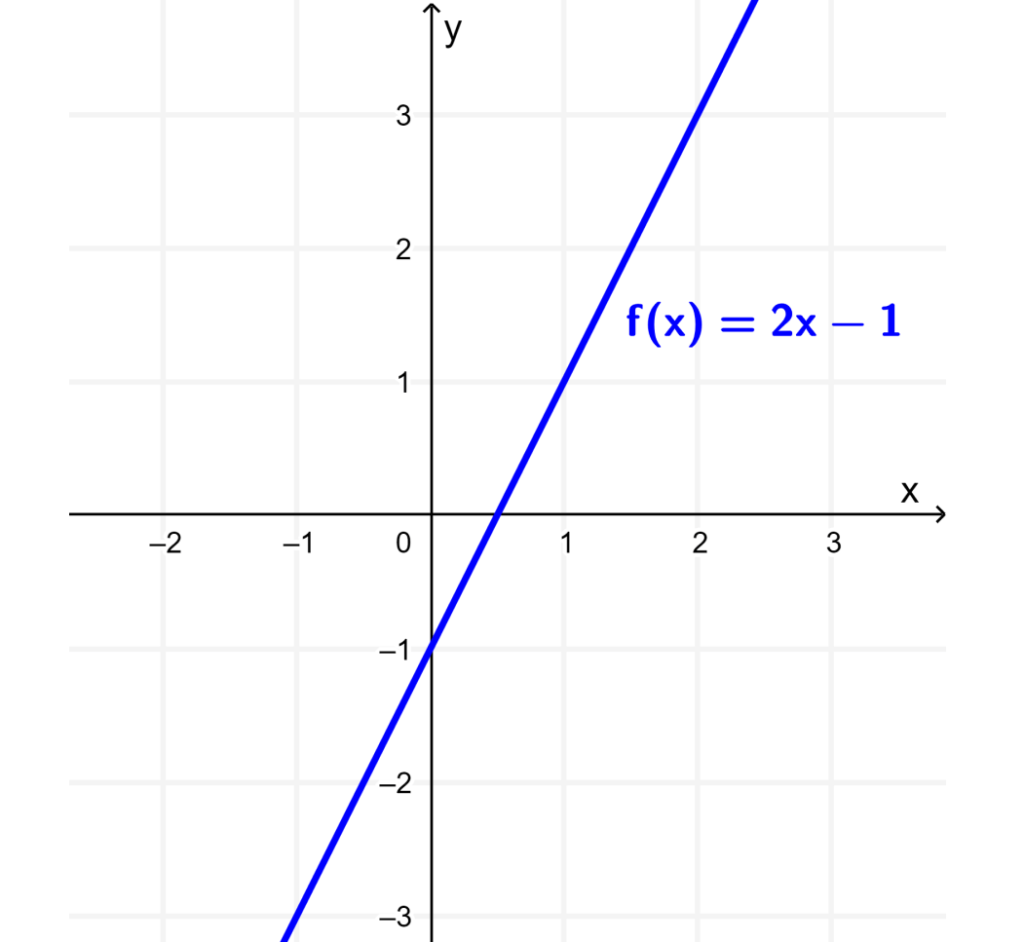
Podemos entender el desplazamiento horizontal de una función al tomar a la función $latex f(x)=2x-1$ como ejemplo. Cuando graficamos esta función, obtenemos la siguiente recta:
Ahora, vamos a aplicar las transformaciones (i) $latex f(x+2)$ y (ii) $latex f(x-2)$. Entonces, usando la función original $latex f(x)=2x-1$ y simplificando las transformaciones, tenemos:
(i) $latex f(x+2)=2(x+2)-1~$ y (ii) $latex f(x-2)=2(x-2)-1$
(i) $latex f(x+2)=2x+3~$ y (ii) $latex f(x-2)=2x-5$
Luego, podemos graficar a las funciones (i) y (ii) usando el mismo plano cartesiano que la función original para comparar sus gráficas. Entonces, tenemos:
En el caso (i), la transformación $latex f(x+2)$ produjo una traslación de 2 unidades hacia la izquierda. Es decir, -2 unidades paralelas al eje x.
En el caso (ii), la transformación $latex f(x-2)$ produjo una traslación de 2 unidades hacia la derecha. Es decir, 2 unidades paralelas al eje x.
En resumen, tenemos:
- La transformación $latex f(x+a)$ resulta en un desplazamiento en la gráfica original de f de $latex a$ unidades hacia la izquierda.
- La transformación $latex f(x-a)$ resulta en un desplazamiento en la gráfica original de f de $latex a$ unidades hacia la derecha.
Determinar el desplazamiento vertical de una función
El desplazamiento vertical de una función es una transformación que hace que la gráfica de la función original sea movida hacia arriba o hacia abajo. Es decir, el desplazamiento sucede paralelo al eje y.
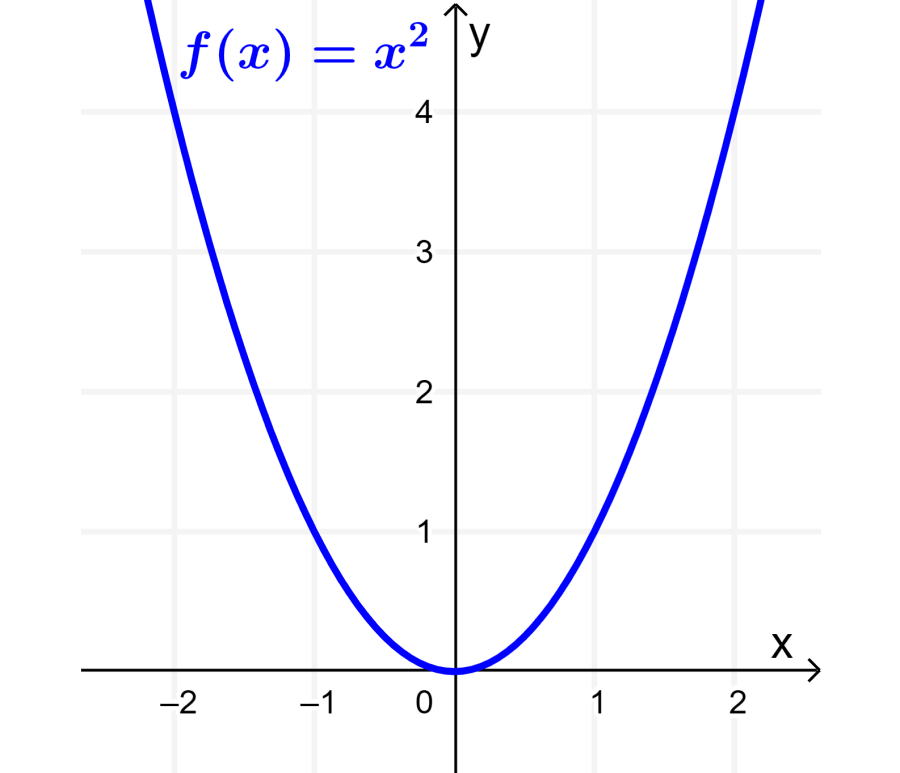
Para entender el desplazamiento vertical de una función, podemos considerar a la función $latex f(x)=x^2$ como ejemplo. Si es que graficamos a esta función, obtenemos la siguiente curva:
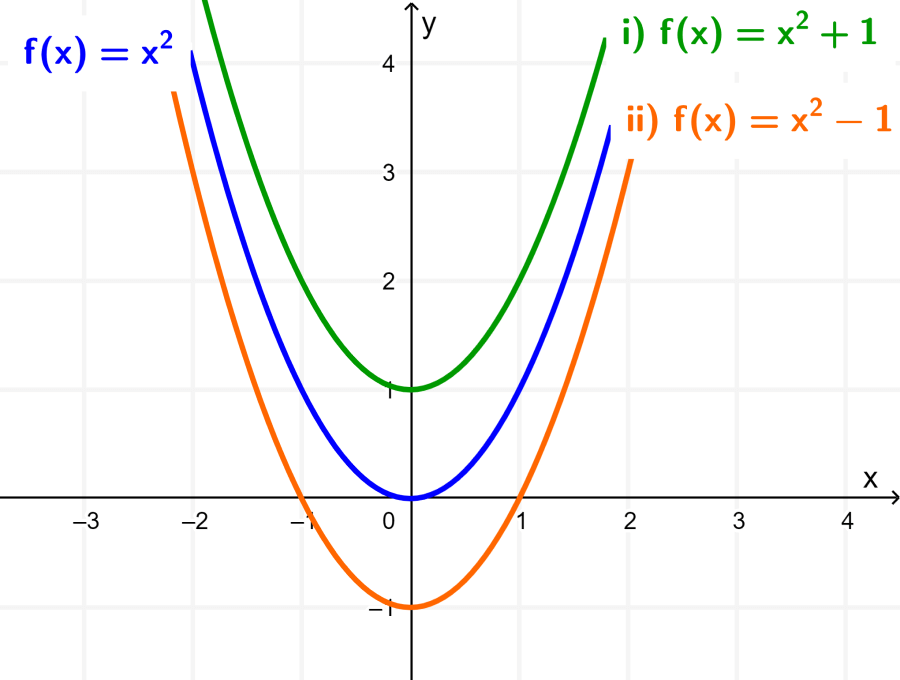
Si es que ahora sumamos y restamos 1 unidad a la función original, tenemos las funciones (i) $latex f(x)+1$ y (ii) $latex f(x)-1$. Simplificando, tenemos:
(i) $latex f(x)+1=x^2+1~$ y (ii) $latex f(x)-1=x^2-1$
Usando el mismo plano cartesiano de la función original $latex f(x)$, podemos graficar las funciones (i) y (ii) para obtener lo siguiente:
Podemos observar que, en el caso (i), la gráfica de f ha sido movida 1 unidad hacia arriba. Es decir, 1 unidad paralela al eje y.
Por otro lado, la gráfica de la función (ii) es igual a la gráfica de f movida 1 unidad hacia abajo. Es decir, -1 unidad paralela al eje y.
En resumen, tenemos lo siguiente:
- La transformación $latex f(x)+a$, produce un desplazamiento en la gráfica original de $latex f(x)$ de $latex a$ unidades hacia arriba.
- La transformación $latex f(x)-a$, produce un desplazamiento en la gráfica original de $latex f(x)$ de $latex a$ unidades hacia abajo.
Ejemplos de desplazamiento horizontal y vertical en funciones
EJEMPLO 1
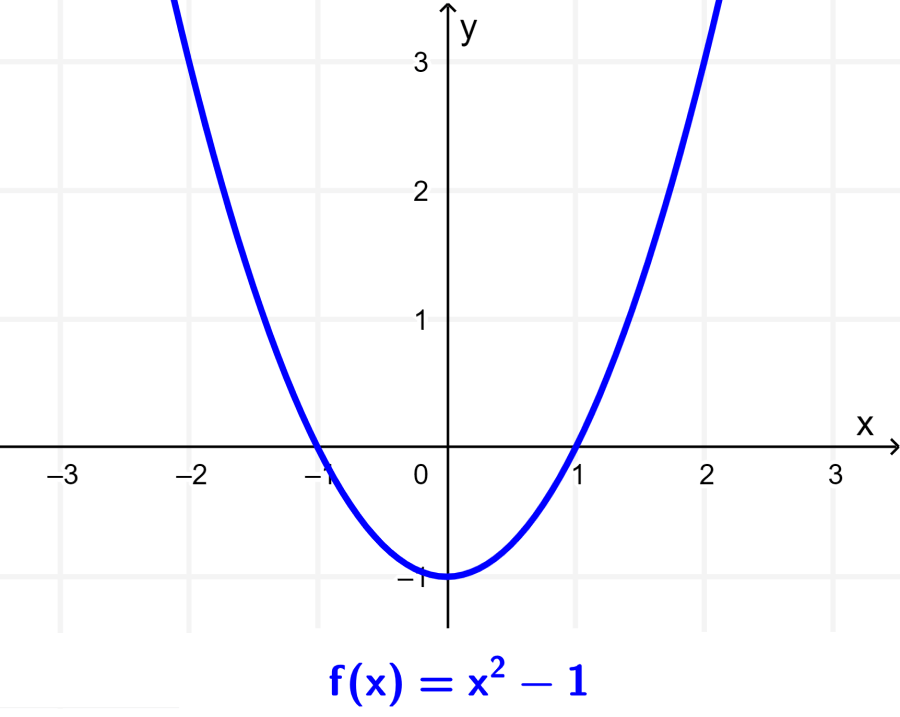
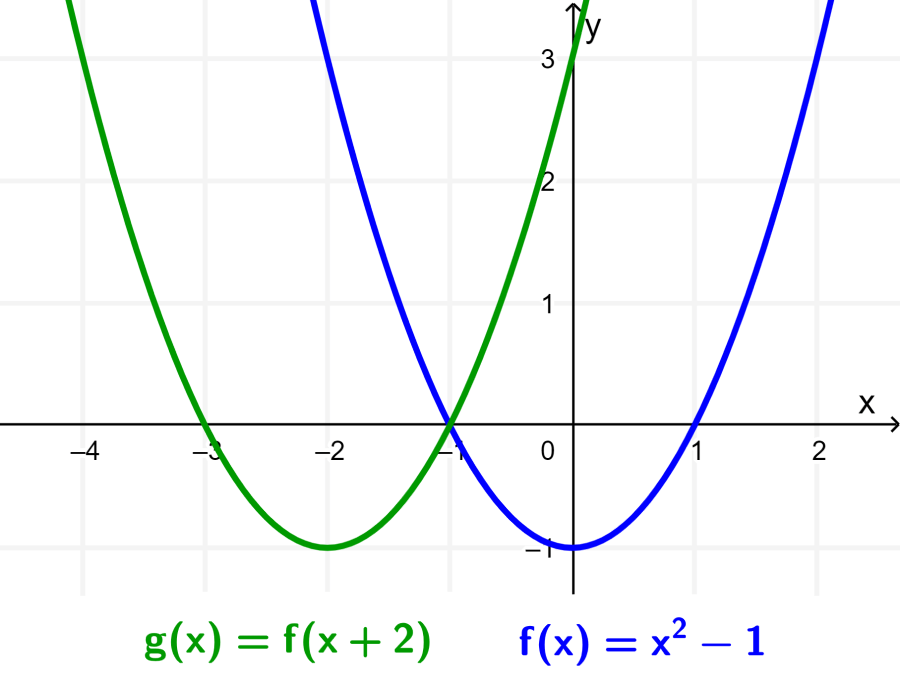
Traza la gráfica de $latex f(x)=x^2-1$. Luego, encuentra la ecuación de la transformación $latex g(x)=f(x+2)$ y grafícala.
Solución
Empezando con la gráfica de $latex f(x)$, tenemos:
Ahora, podemos encontrar la ecuación de la función $latex g(x)$ al aplicar la transformación en la función original y simplificar:
$latex g(x)=f(x+2)$
$latex =(x+2)^2-1$
$latex =x^2+4x+4-1$
$latex =x^2+4x+3$
Podemos graficar la función $latex g(x)$ al considerar que la gráfica de g puede ser obtenida al trasladar a la gráfica de f por 2 unidades hacia la izquierda, es decir, -2 unidades en el eje x.
.
EJEMPLO 2
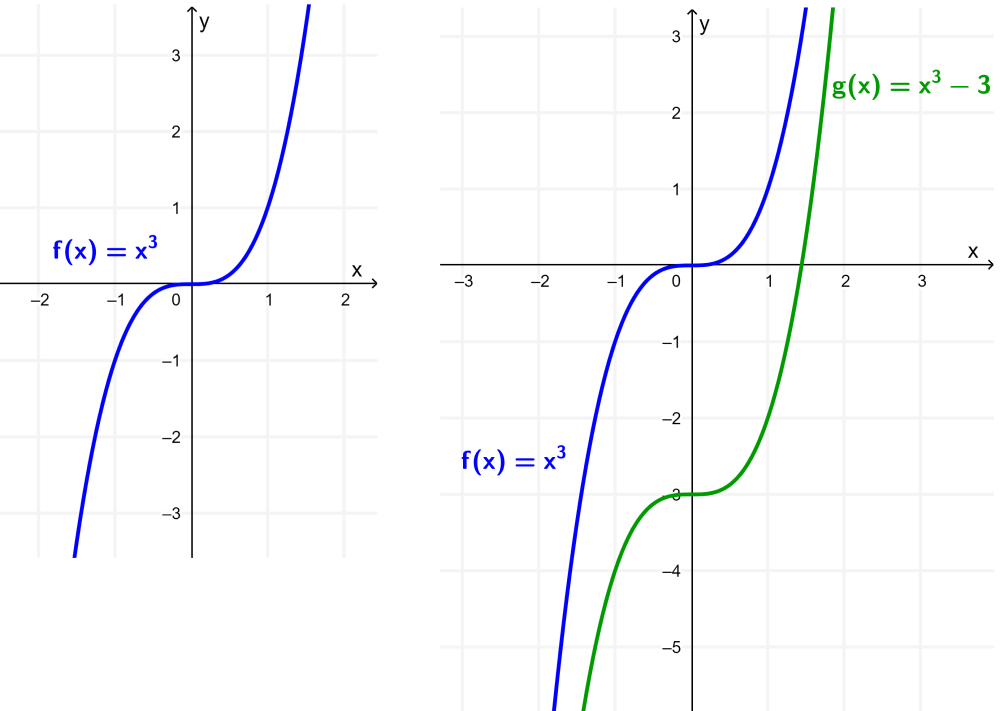
Tenemos a la función $latex f(x)=x^3$. Si es que tenemos la función $latex g(x)=x^3-3$, obtén las gráficas de g y f.
Solución
La función f es la función cúbica base. Esta función es graficada en la parte izquierda del siguiente diagrama.
En el caso de la función g, podemos observar que esta función es equivalente a la función f con un desplazamiento vertical de -3 unidades, como podemos observar en la gráfica derecha del siguiente diagrama.
.
EJEMPLO 3
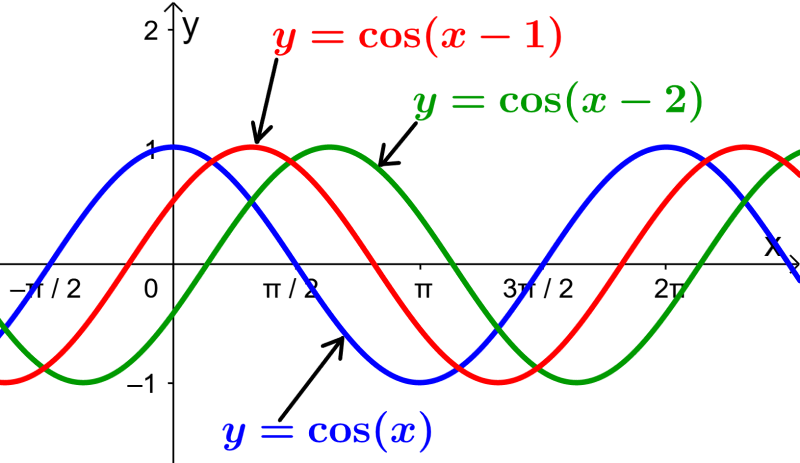
Grafica la función coseno en su forma base. Luego, grafica dos funciones coseno que tengan un desplazamiento de 1 unidad y de 2 unidades hacia la derecha con respecto a la forma base.
Solución
La función coseno base, $latex f(x)=cos(x)$, tiene un valor de 1 cuando x es igual a 0. Además, pasa por el punto (π/2, 0) y tiene un periodo de π.
Para aplicar un desplazamiento de 1 unidad y de 2 unidades hacia la derecha, tenemos que aplicar las transformaciones $latex g(x)=f(x-1)$ y $latex h(x)=f(x-2)$ respectivamente.
Cuando graficamos a las tres funciones, tenemos:
EJEMPLO 4
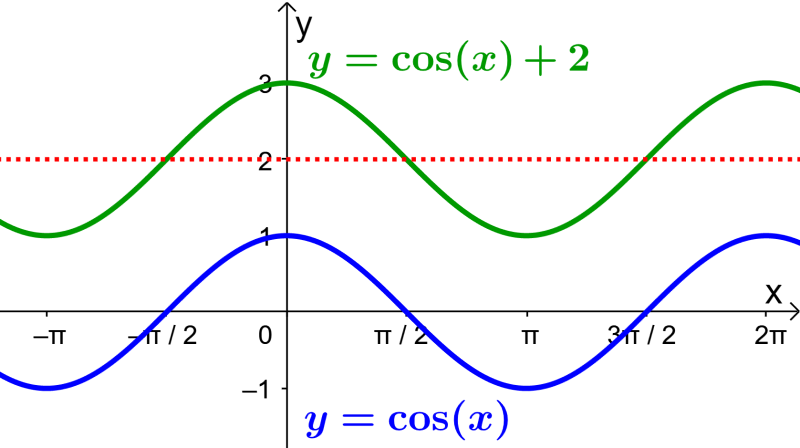
Grafica la función $latex f(x)=\cos(x)+2$.
Solución
Al comparar a la función dada con la función coseno estándar $latex f(x)=\cos(x)$, podemos deducir que un desplazamiento vertical de 2 unidades hacia arriba fue aplicado.
Entonces, podemos graficar a la función $latex f(x)=\cos(x)+2$ al graficar a una función coseno básica y moverla 2 unidades hacia arriba:
EJEMPLO 5
Obtén la gráfica de $latex g(x)=|x-2|$.
Solución
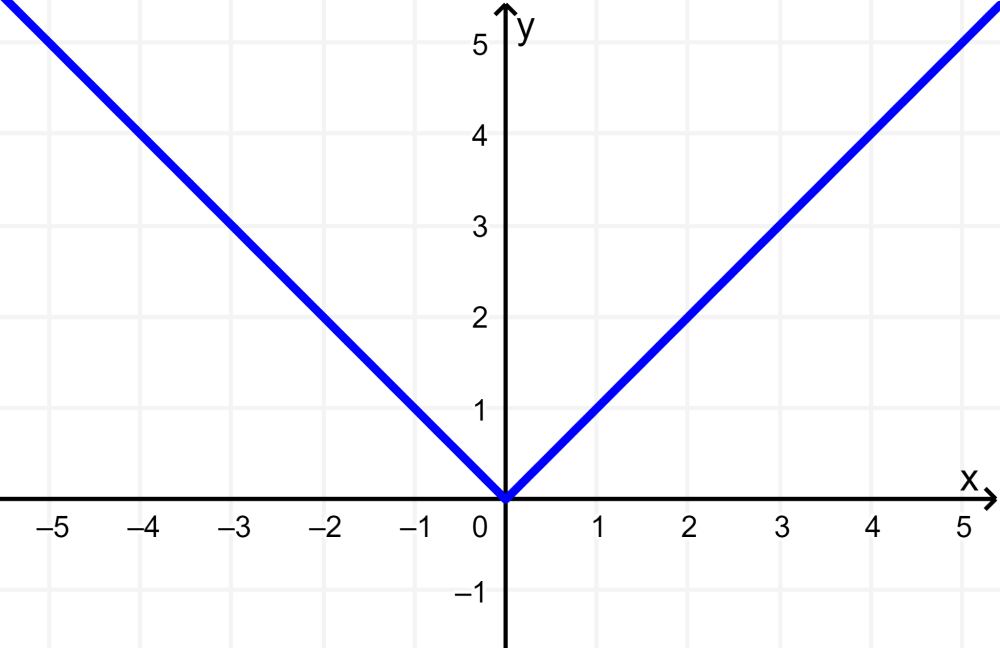
En este ejemplo, tenemos a la función valor absoluto. En su forma base, $latex f(x)=|x|$, la gráfica de la función valor absoluto es:
Entonces, la gráfica de $latex g(x)=|x-2|$ puede ser obtenida al desplazar 2 unidades hacia la derecha a la gráfica de la función valor absoluto en su forma base:
.
EJEMPLO 6
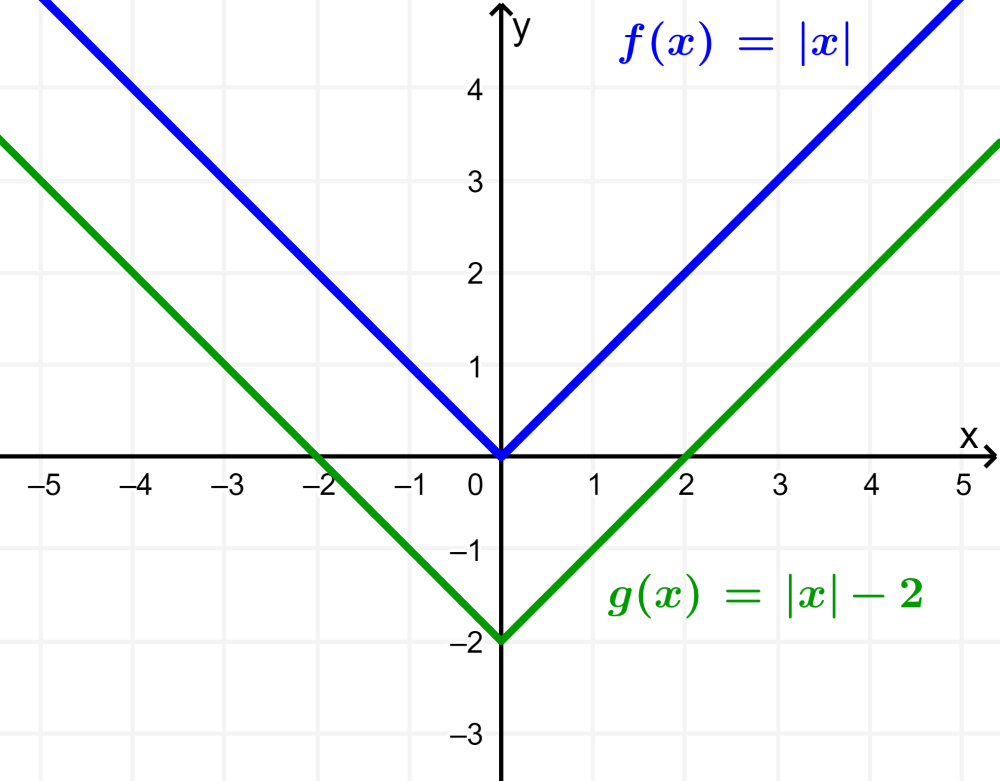
¿Cuál es la gráfica de $latex g(x)=|x|-2$?
Solución
Aquí, tenemos a la función valor absoluto. En su forma base, $latex f(x)=|x|$, la gráfica de la función valor absoluto es la siguiente:
Entonces, podemos obtener la gráfica de $latex g(x)=|x|-2$ si es que movemos a la gráfica de la función valor absoluto base 2 unidades hacia abajo:
.
EJEMPLO 7
¿Qué transformación necesitamos aplicar para desplazar a la función $latex f(x)=\tan(5x-2)$ -4 unidades paralelas al eje x?
Solución
Un desplazamiento de -4 unidades paralelas al eje x es equivalente a aplicar un desplazamiento de 4 unidades hacia la izquierda.
Podemos realizar este desplazamiento al aplicar la transformación $latex f(x-4)$. En este caso, tenemos la función $latex f(x)=\tan(5x-2)$. Entonces, tenemos:
$latex f(x-4)=\tan(5(x-4)-2)$
$latex f(x-4)=\tan(5x-20-2)$
$latex f(x-4)=\tan(5x-22)$
EJEMPLO 8
¿Qué cambios necesitamos realizar a la función $latex f(x)=\tan(5x-2)$ si es que queremos desplazarla -5 unidades paralelas al eje y?
Solución
Un desplazamiento de -5 unidades paralelas al eje y es lo mismo que aplicar un desplazamiento de 5 unidades hacia abajo en la función original.
Para realizar este desplazamiento, aplicamos la transformación $latex f(x)-5$. En este caso, tenemos la función $latex f(x)=\tan(5x-2)$. Entonces, tenemos:
$latex f(x)-5=\tan(5x-2)-5$
Ejercicios de desplazamiento horizontal y vertical para resolver
¿Cuál función tiene un desplazamiento de 6 unidades hacia arriba con respecto a la función $latex f(x)=-2x-3$?
Escribe la respuesta en la casilla.
Véase también
¿Interesado en aprender más sobre transformaciones de funciones? Mira estas páginas: