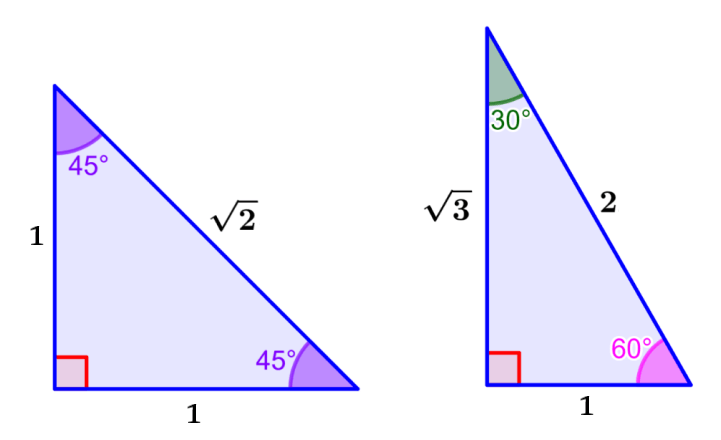
Los ángulos notables son ángulos que tienen valores que son comunes en ejercicios de trigonometría y en la vida cotidiana en general. Generalmente, los ángulos notables son los ángulos de 30°, 45° y 60°. Estos ángulos tienen razones trigonométricas que son fáciles de recordar.
A continuación, conoceremos las razones trigonométricas de los ángulos notables de 30°, 45° y 60°. Además, aprenderemos cómo derivar estas razones trigonométricas.
GEOMETRÍA
Relevante para…
Aprender sobre las razones trigonométricas de ángulos notables.
GEOMETRÍA
Relevante para…
Aprender sobre las razones trigonométricas de ángulos notables.
Razones trigonométricas de 45°
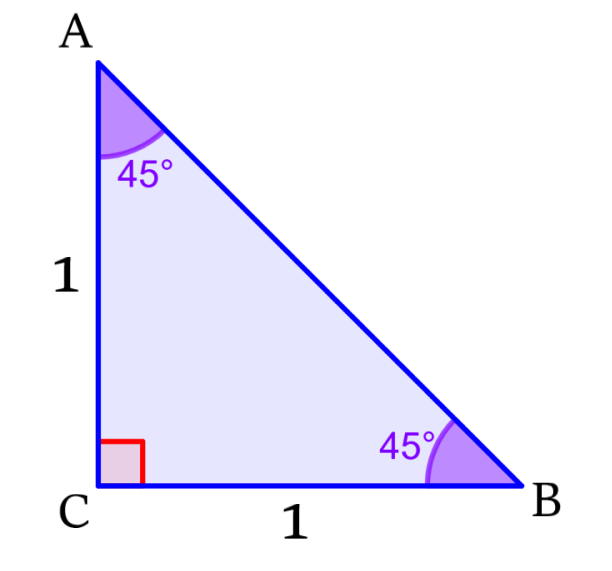
Para encontrar las razones trigonométricas de un ángulo de 45°, podemos considerar al siguiente triángulo rectángulo isósceles:
Este triángulo tiene dos ángulos con las mismas medidas, por lo que sus dos catetos tienen la misma longitud de 1 unidad.
Podemos usar el teorema de Pitágoras para encontrar la longitud de la hipotenusa:
$latex {{AB}^2}={{BC}^2}+{{AC}^2}$
$latex {{AB}^2}={{1}^2}+{{1}^2}$
$latex {{AB}^2}=2$
$latex AB=\sqrt{2}$
Ahora, podemos usar el mismo triángulo para obtener los valores de las razones trigonométricas, seno, coseno y tangente:
Usando la definición del seno (lado opuesto sobre hipotenusa), tenemos:
$$\sin(45^{\circ})=\frac{AC}{AB}=\frac{1}{\sqrt{2}}$$
Usando la definición del coseno (lado adyacente sobre hipotenusa), tenemos:
$$\cos(45^{\circ})=\frac{BC}{AB}=\frac{1}{\sqrt{2}}$$
Usando la definición de la tangente (lado opuesto sobre lado adyacente), tenemos:
$$\tan(45^{\circ})=\frac{AC}{BC}=1$$
En resumen, tenemos lo siguiente:
| $$\sin(45^{\circ})=\frac{1}{\sqrt{2}}$$ $$\cos(45^{\circ})=\frac{1}{\sqrt{2}}$$ $$\tan(45^{\circ})=1$$ |
Razones trigonométricas de 30°
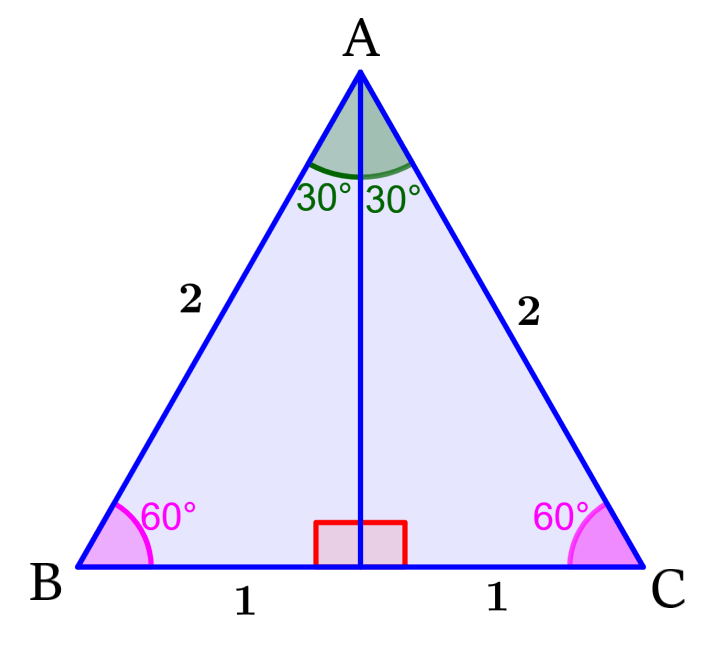
Para encontrar las razones trigonométricas del ángulo de 30°, vamos a usar un triángulo equilátero que tiene lados con una longitud de 2 unidades.
D es el punto en donde el segmento perpendicular desde A se encuentra con la base. El segmento AD divide al triángulo equilátero en dos triángulos iguales que tienen los ángulos 30°, 60° y 90°.
Podemos encontrar la longitud del segmento AD usando el teorema de Pitágoras:
$latex {{AD}^2}+{{BD}^2}={{AB}^2}$
$latex {{AD}^2}+{{1}^2}={{2}^2}$
$latex {{AD}^2}+1=4$
$latex {{AD}^2}=3$
$latex AD=\sqrt{3}$
Usando la definición del seno (lado opuesto sobre hipotenusa), tenemos:
$$\sin(30^{\circ})=\frac{BD}{AB}=\frac{1}{2}$$
Usando la definición del coseno (lado adyacente sobre hipotenusa), tenemos:
$$\cos(30^{\circ})=\frac{AD}{AB}=\frac{\sqrt{3}}{2}$$
Usando la definición de la tangente (lado opuesto sobre lado adyacente), tenemos:
$$\tan(30^{\circ})=\frac{BD}{AD}=\frac{1}{\sqrt{3}}$$
En resumen, tenemos lo siguiente:
| $$\sin(30^{\circ})=\frac{1}{2}$$ $$\cos(30^{\circ})=\frac{\sqrt{3}}{2}$$ $$\tan(30^{\circ})=\frac{1}{\sqrt{3}}$$ |
Razones trigonométricas de 60°
Podemos encontrar las razones trigonométricas del ángulo de 60° usando el mismo triángulo que usamos para encontrar las razones trigonométricas de 30°.
Entonces, usamos las longitudes $latex AB=2$, $latex BD=1$ y $latex AD=\sqrt{3}$ con las funciones trigonométricas seno, coseno y tangente.
Usando la definición del seno (lado opuesto sobre hipotenusa), tenemos:
$$\sin(60^{\circ})=\frac{AD}{AB}=\frac{\sqrt{3}}{2}$$
Usando la definición del coseno (lado adyacente sobre hipotenusa), tenemos:
$$\cos(60^{\circ})=\frac{BD}{AB}=\frac{1}{2}$$
Usando la definición de la tangente (lado opuesto sobre lado adyacente), tenemos:
$$\tan(60^{\circ})=\frac{AD}{BD}=\sqrt{3}$$
En resumen, tenemos lo siguiente:
| $$\sin(60^{\circ})=\frac{\sqrt{3}}{2}$$ $$\cos(60^{\circ})=\frac{1}{2}$$ $$\tan(60^{\circ})=\sqrt{3}$$ |
Tabla de las razones trigonométricas de ángulos notables
Las razones trigonométricas de los ángulos 30°, 45° y 60° están resumidos en la siguiente tabla:
| Razón | θ = 30° | θ = 30° | θ = 30° |
| sin θ | $latex \frac{1}{2}$ | $latex \frac{1}{\sqrt{2}}$ | $latex \frac{\sqrt{3}}{2}$ |
| cos θ | $latex \frac{\sqrt{3}}{2}$ | $latex \frac{1}{\sqrt{2}}$ | $latex \frac{1}{2}$ |
| tan θ | $latex \frac{1}{\sqrt{3}}$ | 1 | $latex \sqrt{3}$ |
Es recomendable memorizarse estas razones trigonométricas, ya que varios problemas encontrados en trigonometría usan los ángulos 30°, 45° y 60°.
Véase también
¿Interesado en aprender más sobre ángulos y triángulos especiales? Mira estas páginas: