Los triángulos semejantes se caracterizan por tener lados correspondientes con las mismas proporciones, pero no necesariamente con las mismas medidas. Por otro lado, los triángulos congruentes tienen lados correspondientes con las mismas medidas. Esto significa que los triángulos congruentes comparten la misma forma y el mismo tamaño, mientras que los triángulos semejantes solo comparten la misma forma.
A continuación, conoceremos más detalles sobre triángulos semejantes y congruentes.
Definiciones de triángulos semejantes y triángulos congruentes
Congruencia de dos figuras significa que las figuras son exactamente las mismas. Por ejemplo, cuando tenemos dos segmentos de línea con la misma longitud, los segmentos son congruentes.
De igual forma, para que dos figuras geométricas sean congruentes, deben tener la misma forma y el mismo tamaño.
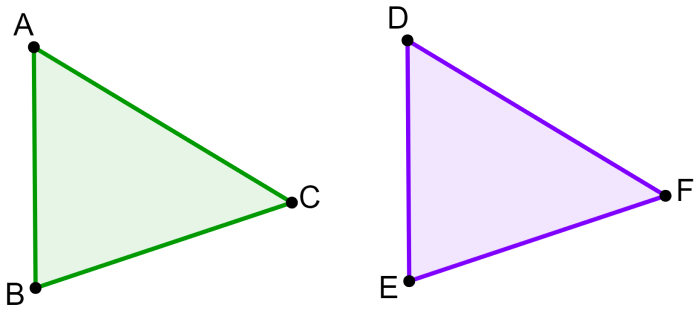
Los triángulos ABC y DEF son congruentes. Podemos ver que estos triángulos son exactamente iguales. Los triángulos tienen la misma forma y el mismo tamaño. Entonces, todas las longitudes de sus lados son iguales, al igual que todas las medidas de sus ángulos.
Para que dos figuras sean semejantes, deben tener la misma forma, pero no necesariamente el mismo tamaño. Entonces, las figuras semejantes no son congruentes.
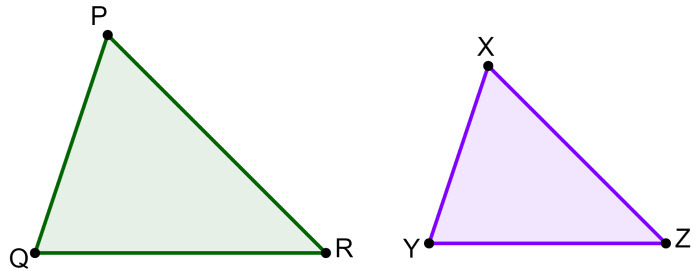
Los triángulos PQR y XYZ son semejantes. Podemos ver que tienen exactamente la misma forma, pero tienen tamaños diferentes.
Criterios de triángulos congruentes
Para que dos triángulos sean congruentes, deben cumplir con uno de los siguientes criterios:
(Lado, lado, lado): Los tres pares de lados correspondientes son iguales.
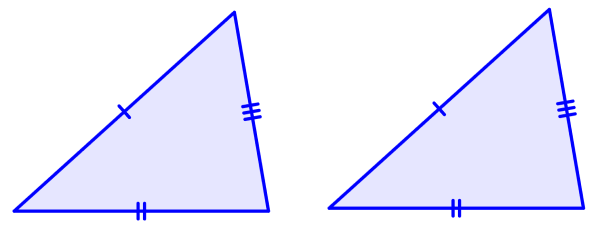
(Lado, ángulo, lado): Dos pares de lados correspondientes y los ángulos entre esos lados son iguales.
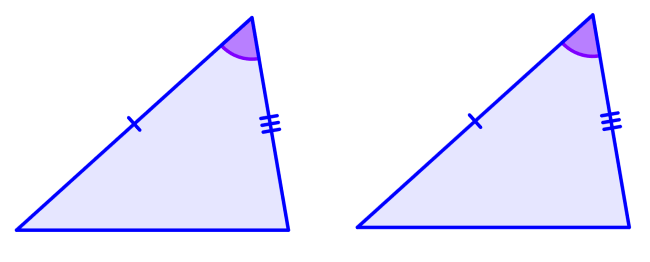
(Ángulo, lado, ángulo): Dos pares de ángulos correspondientes y los lados entre esos ángulos son iguales.
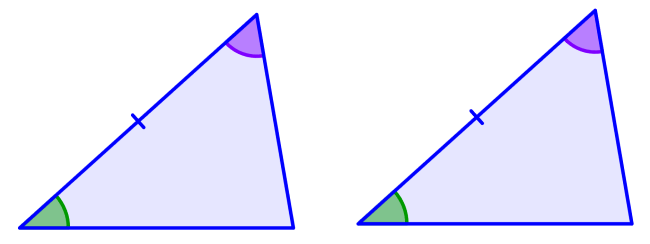
(Ángulo, ángulo, lado): Dos pares de ángulos correspondientes y un par de lados correspondientes, que no están entre los ángulos, son iguales
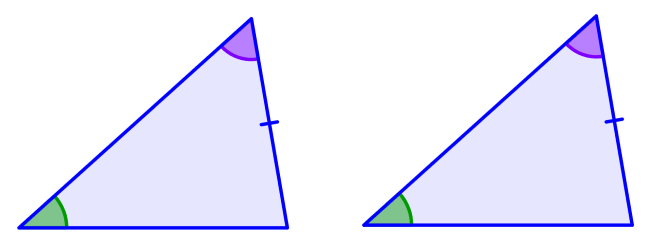
(Hipotenusa, lado): En triángulos rectángulos, las hipotenusas son iguales y otro par de lados correspondientes son iguales.
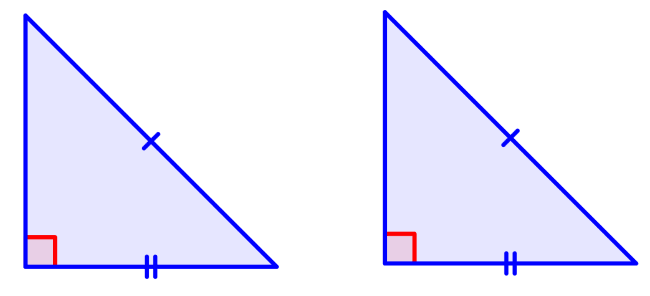
Criterios de triángulos semejantes
Para que dos triángulos sean semejantes, deben cumplir con uno de los siguientes criterios:
(Ángulo, ángulo): Dos pares de ángulos correspondientes son iguales.
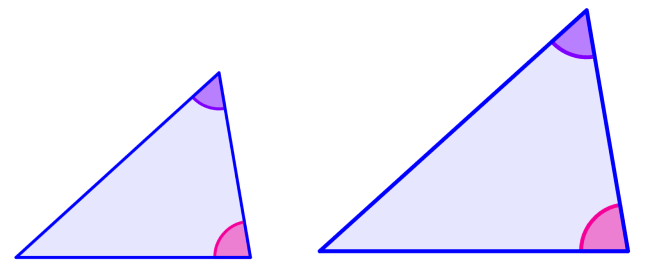
(Lado, lado, lado): Los tres pares de lados correspondientes tienen las mismas proporciones.
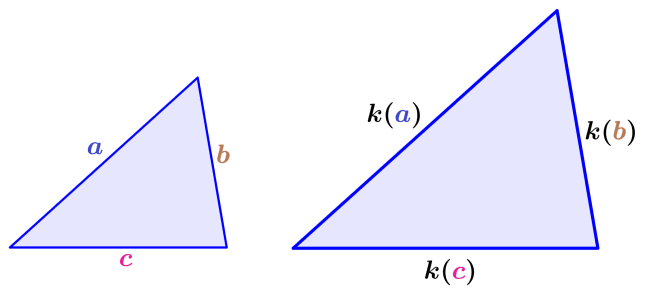
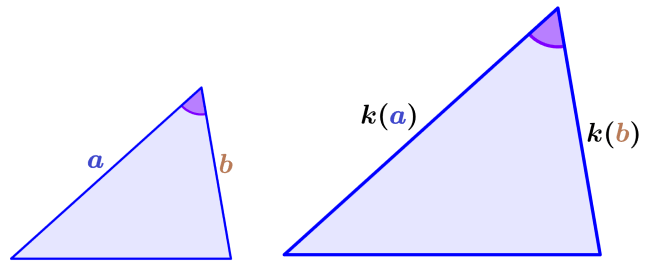
(Lado, ángulo, lado): Dos pares de lados correspondientes son proporcionales y los ángulos entre ellos son iguales.
Ejercicios resueltos de triángulos semejantes y congruentes
EJERCICIO 1
Determina si es los siguientes triángulos son semejantes, congruentes o ninguno.
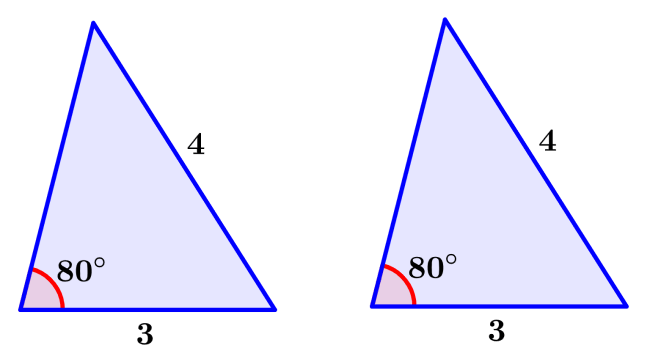
Solución: Conocemos las medidas de dos lados correspondientes de los triángulos. Vemos que esas medidas son las mismas. Además, conocemos la medida de un par de ángulos correspondientes.
Sin embargo, el ángulo que conocemos es opuesto a uno de los lados que también conocemos. No conocemos ni la medida del tercer lado, ni su ángulo opuesto, por lo que no podemos determinar si los triángulos son semejantes o congruentes.
EJERCICIO 2
¿Los siguientes triángulos son semejantes, congruentes o ninguno?
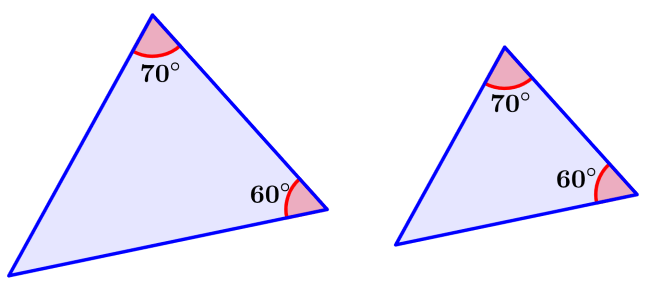
Solución: Conocemos las medidas de dos pares de ángulos correspondientes. Las medidas son las mismas. Esto significa que los triángulos son semejantes. No podemos determinar si los triángulos son congruentes, ya que no conocemos las medidas de sus lados.
EJERCICIO 3
Determina si los triángulos son semejantes, congruentes o ninguno.
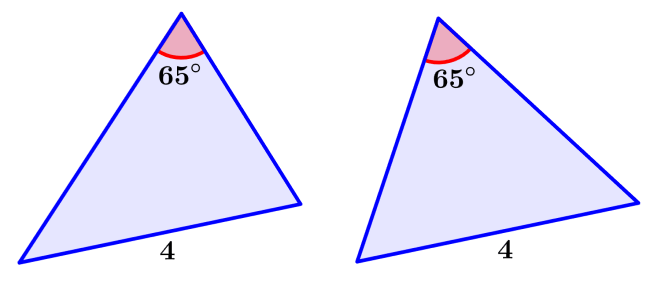
Solución: Conocemos las medidas de un par de ángulos correspondientes y las longitudes de un par de lados correspondientes. Los lados son opuestos al ángulo conocido. Por lo tanto, no podemos determinar si estos triángulos son semejantes o congruentes.
Véase también
¿Interesado en aprender más sobre triángulos y la desigualdad triangular? Mira estas páginas:


