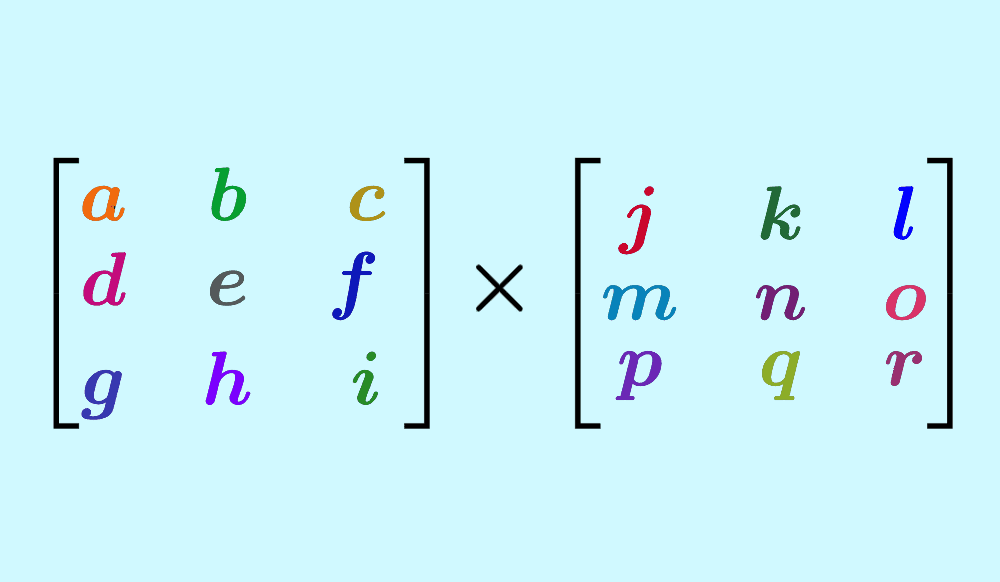Junto con el álgebra lineal, las matrices han demostrado ser una poderosa herramienta para resolver infinidad de problemas en diversos campos. Sus propiedades únicas y sus amplias aplicaciones las han convertido en un tema esencial para investigadores, profesionales y estudiantes por igual.
En este artículo, nos enfocaremos en el fascinante mundo de las matrices, explorando sus propiedades fundamentales y conociendo algunas de sus innumerables aplicaciones.
¿Cuáles son las propiedades de las matrices?
Las matrices son matrices rectangulares de números, símbolos o expresiones dispuestas en filas y columnas. Estas son algunas de las propiedades clave de las matrices:
1. Dimensiones
Una matriz se caracteriza por sus dimensiones, típicamente denotadas como m x n, donde m es el número de filas y n es el número de columnas. Por ejemplo, una matriz de 3×2 tiene 3 filas y 2 columnas.
2. Igualdad
Dos matrices son iguales si tienen las mismas dimensiones y sus elementos correspondientes son iguales.
3. Suma
Las matrices pueden sumarse si tienen las mismas dimensiones. La suma de dos matrices se obtiene sumando sus elementos correspondientes.
4. Multiplicación escalar
Una matriz puede multiplicarse por un escalar (un solo número). El producto se obtiene multiplicando cada elemento de la matriz por el escalar.
5. Multiplicación de matrices
Dos matrices pueden multiplicarse si el número de columnas de la primera matriz es igual al número de filas de la segunda matriz. El producto es una nueva matriz con dimensiones iguales al número de filas de la primera matriz y al número de columnas de la segunda matriz.
6. Transposición
La transposición de una matriz se obtiene intercambiando sus filas y columnas. Por ejemplo, si A es una matriz m x n, su transpuesta AT es una matriz n x m.
7. Determinante
El determinante es un valor escalar que puede calcularse para matrices cuadradas (matrices con igual número de filas y columnas). Tiene propiedades y aplicaciones importantes, como determinar si una matriz es invertible.
8. Inversa
Una matriz cuadrada A es invertible si existe una matriz B tal que AB = BA = I, donde I es la matriz identidad (una matriz cuadrada con 1s en la diagonal y 0s en el resto). La matriz B se denomina inversa de A y se denota como A-1.
9. Rango
El rango de una matriz es el número máximo de filas o columnas linealmente independientes. Proporciona información sobre la dimensión del espacio de columnas y el espacio de filas, que son importantes para resolver sistemas lineales de ecuaciones.
10. Traza
La traza de una matriz cuadrada es la suma de sus elementos diagonales. Es una propiedad importante que se utiliza en diversas operaciones y demostraciones matemáticas.
11. Matrices simétricas y asimétricas
Una matriz es simétrica si su transpuesta es igual a la matriz original (AT = A). Una matriz es asimétrica si su transpuesta es igual al negativo de la matriz original (AT = -A).
12. Matrices ortogonales y ortonormales
Una matriz cuadrada es ortogonal si sus columnas (y filas) son ortogonales por pares y tienen longitud unitaria. Es decir, una matriz ortogonal cumple la condición AT × A = I.
Si las columnas (y filas) también son ortogonales (es decir, forman una base ortonormal), la matriz se denomina ortonormal.
¿Cuáles son las aplicaciones de las matrices?
Las matrices tienen una gran variedad de aplicaciones en diversos campos, como las matemáticas, la física, la ingeniería, la informática y la economía, entre otros.
Algunas de las aplicaciones más comunes de las matrices son:
1. Sistemas lineales de ecuaciones
Las matrices proporcionan una representación compacta de los sistemas lineales de ecuaciones y se utilizan para resolverlos mediante métodos como la eliminación de Gauss, la regla de Cramer y la inversión matricial.
2. Transformaciones lineales
En álgebra lineal, las matrices pueden representar transformaciones lineales, que son funciones que asignan vectores de un espacio vectorial a otro conservando su estructura lineal.
3. Gráficos de computadoras
Las matrices se utilizan en los gráficos de computadoras para representar transformaciones como la traslación, el escalado, la rotación y la proyección. Ayudan a manipular y representar modelos 3D en pantallas 2D.
4. Procesamiento de señales
Las matrices son aplicadas para representar señales y sistemas en el procesamiento digital de señales, incluido el procesamiento de imágenes, el procesamiento de audio y los sistemas de comunicación.
Las matrices se utilizan para realizar operaciones como filtrado, transformaciones de Fourier y transformaciones wavelet.
5. Teoría del control
En la teoría del control, las matrices ayudan a representar la dinámica de los sistemas y diseñar controladores que regulen su comportamiento.
Por ejemplo, la representación del espacio de estados, una popular técnica de modelado, utiliza matrices para describir las relaciones entre las entradas, las salidas y los estados internos de un sistema.
6. Optimización
Varios problemas de optimización, como la programación lineal, la programación cuadrática y la optimización convexa, pueden ser resueltos usando matrices.
Esto permite encontrar la mejor solución bajo unas restricciones dadas.
7. Criptografía
Las matrices desempeñan un papel importante en varios algoritmos criptográficos, como el cifrado de Hill y la criptografía basada en celosías, que se basan en operaciones matriciales para proporcionar seguridad.
8. Aprendizaje automático y minería de datos
Las matrices se utilizan para representar datos y realizar operaciones como el análisis de componentes principales (PCA), la descomposición de valores singulares (SVD) y la factorización de matrices, que son técnicas esenciales en el aprendizaje automático, la minería de datos y los sistemas de recomendación.
9. Mecánica cuántica
En mecánica cuántica se utilizan matrices para representar estados y operadores cuánticos, lo que da lugar a una formulación conocida como mecánica matricial. Este enfoque es esencial para comprender y predecir el comportamiento de los sistemas cuánticos.
10. Análisis de elementos finitos
Las matrices son aplicadas en el análisis de elementos finitos para modelar y resolver problemas complejos de ingeniería y física, como el análisis estructural, la dinámica de fluidos y la transferencia de calor.
11. Economía y finanzas
En economía y finanzas, las matrices son aplicadas para modelar y analizar diversos problemas, como la optimización de carteras y la teoría de juegos.
Estos son sólo algunos ejemplos de la amplia gama de aplicaciones de las matrices. Su versatilidad las convierten en una herramienta fundamental en muchas áreas de la ciencia, la ingeniería y más.
Véase también
¿Interesado en aprender más sobre matrices? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
