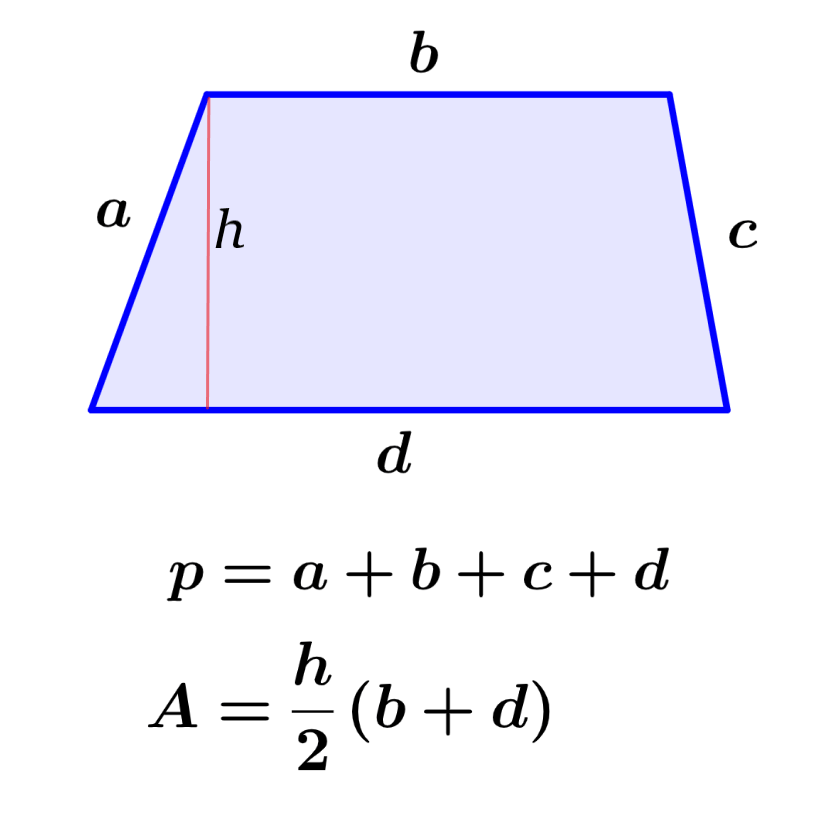
El perímetro de un trapecio es la longitud total del contorno del trapecio. Por otro lado, el área es una medida del espacio ocupado por el trapecio. Podemos calcular el perímetro de un trapecio al sumar las longitudes de todos sus lados y podemos calcular su área al sumar sus bases, multiplicar por su altura y dividir por 2.
A continuación, aprenderemos todo lo relacionado sobre el perímetro y el área de un trapecio. Conoceremos sus fórmulas y las usaremos para resolver algunos ejercicios de práctica.
¿Cómo calcular el perímetro de un trapecio?
Para calcular el perímetro de un trapecio, tenemos que sumar la longitud de todos sus lados. Entonces, la fórmula del perímetro de un trapecio es:
| $latex p=a+b+c+d$ |
en donde, “a, b, c, d” representan a las longitudes de los lados del trapecio.
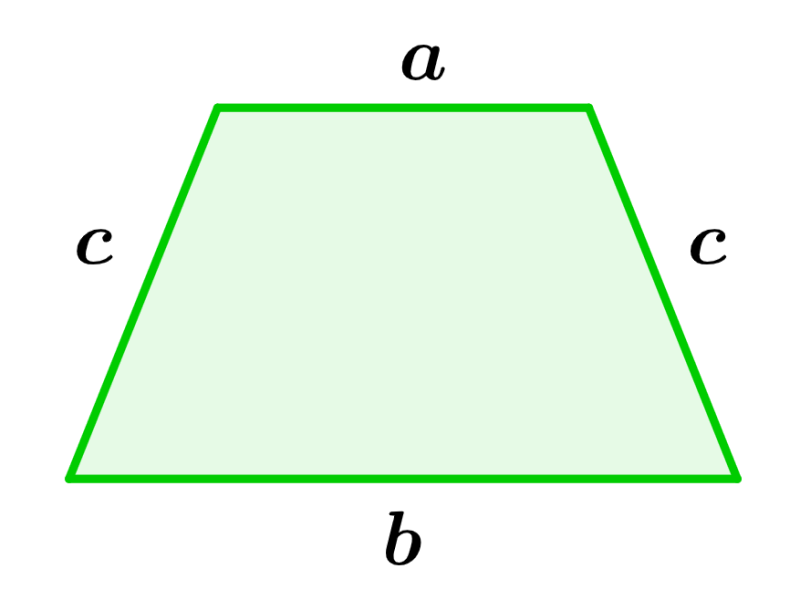
Perímetro de un trapecio isósceles
En un trapecio isósceles, dos de sus lados tienen la misma longitud, entonces, podemos calcular su perímetro con la siguiente fórmula:
| $latex p=a+b+2c$ |
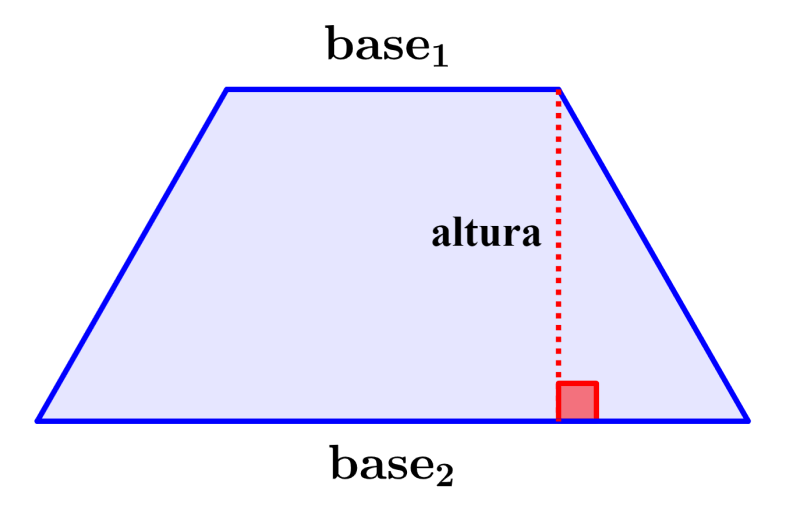
¿Cómo calcular el área de un trapecio?
Para encontrar el área de un trapecio, tenemos que sumar las longitudes de sus bases. Luego, multiplicamos a esa suma por la altura del trapecio y dividimos el resultado por 2. Entonces, la fórmula para el área del trapecio es:
| $latex A=\frac{(b_{1}+b_{2})h}{2}$ |
en donde,
- $latex b_{1}=$ la longitud una base del trapecio
- $latex b_{2}=$ la longitud de la otra base del trapecio
- $latex h=$ la altura del trapecio
Demostración de la fórmula del área de un trapecio
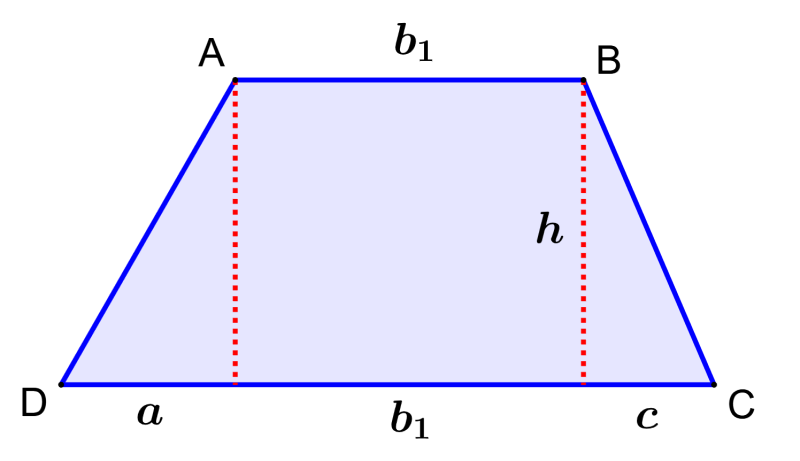
Podemos demostrar la fórmula del área de un trapecio usando el siguiente diagrama:
El trapecio puede ser dividido en dos triángulos rectángulos y en un rectángulo. El área del trapecio es igual a la suma de las áreas de los dos triángulos y el área del rectángulo. Entonces, tenemos que:
área de trapecio = área de triángulo 1 + área de rectángulo + área de triángulo 2
$$A=\frac{ah}{2}+b_{1}h+\frac{ch}{2}$$
$$A=\frac{ah+2b_{1}h+ch}{2}$$
Reorganizando los términos y simplificando, tenemos:
$$A=\frac{h}{2}(b_{1}+(a+b_{1}+c))$$
Ahora, vamos a usar $latex b_{2}$ para representar a la base más larga del trapecio:
$latex b_{2}=a+b_{1}+c$
Sustituyendo esto en la anterior ecuación, tenemos:
$latex A=\frac{h}{2}(b_{1}+b_{2})$
Perímetro y área de un trapecio – Ejercicios resueltos
EJERCICIO 1
Si es que un trapecio tiene lados de longitud 6 cm, 8 cm, 5 cm y 7 cm, ¿cuál es su perímetro?
Solución
Usamos la fórmula del perímetro de un trapecio con las longitudes dadas:
$latex p=a+b+c+d$
$latex p=6+8+5+7$
$latex p=26$
El perímetro del trapecio es igual a 26 cm.
EJERCICIO 2
¿Cuál es el área de un trapecio que tiene bases con longitudes 8 cm y 12 cm y una altura de 10 cm?
Solución
Tenemos la siguiente información:
- Base 1, $latex b_{1}=8$ cm
- Base 2, $latex b_{2}=12$ cm
- Altura, $latex h=10$ cm
Al usar la fórmula del área, tenemos:
$$A=\frac{(b_{1}+b_{2})h}{2}$$
$$=\frac{(8+12)10}{2}$$
$$=\frac{(20)(10)}{2}$$
$$=\frac{200}{2}$$
$latex A=100$
El área del trapecio es igual a 100 cm².
EJERCICIO 3
Encuentra el perímetro de un trapecio que tiene lados con longitudes 12 mm, 14 mm, 7 mm y 9 mm.
Solución
Reemplazando las longitudes dadas en la fórmula del perímetro, tenemos:
$latex p=a+b+c+d$
$latex p=12+14+7+9$
$latex p=42$
El perímetro del trapecio es igual a 42 mm.
EJERCICIO 4
Determina el área de un trapecio que tiene bases con longitudes 11 cm y 15 cm y una altura de 12 cm.
Solución
Tenemos lo siguiente:
- Base 1, $latex b_{1}=11$ cm
- Base 2, $latex b_{2}=15$ cm
- Altura, $latex h=12$ cm
Al aplicar estos valores en la fórmula del área, tenemos:
$$A=\frac{(b_{1}+b_{2})h}{2}$$
$$=\frac{(11+15)12}{2}$$
$$=\frac{(26)(12)}{2}$$
$$ =\frac{312}{2}$$
$latex A=156$
El área del trapecio es 156 cm².
EJERCICIO 5
Un trapecio isósceles tiene dos lados paralelos que miden 11 mm y 13 mm. Si es que los lados laterales del trapecio miden 9 mm, ¿cuál es su perímetro?
Solución
Un trapecio isósceles tiene dos lados iguales, es decir, tenemos c=9. Entonces, tenemos:
$latex p=a+b+2c$
$latex p=11+13+2(9)$
$latex p=24+18$
$latex p=42$
El perímetro del trapecio es igual a 42 mm.
EJERCICIO 6
Encuentra la altura de un trapecio que tiene un área de 200 cm², una base de 9 cm y la otra base de 11 cm.
Solución
Tenemos lo siguiente:
- Área, $latex A=200$ cm²
- Base 1, $latex b_{1}=9$ cm
- Base 2, $latex b_{2}=11$ cm
En este caso, tenemos que usar la fórmula del área y resolver para la altura:
$$A=\frac{(b_{1}+b_{2})h}{2}$$
$$200=\frac{(9+11)h}{2}$$
$latex 400=(9+11)h$
$latex 400=20h$
$latex h=20$
La altura del trapecio mide 20 cm.
EJERCICIO 7
Un trapecio tiene un perímetro de 86 cm y tiene tres lados que miden 21 cm, 23 cm y 25 cm. Determina la longitud del cuarto lado.
Solución
En este caso, tenemos que usar la fórmula del perímetro con el perímetro y las longitudes dadas y vamos a resolver para el cuarto lado:
$latex p=a+b+c+d$
$latex 86=21+23+25+d$
$latex d=86-21-23-25$
$latex d=17$
La longitud del cuarto lado es 17 cm.
EJERCICIO 8
Si es que un trapecio tiene un área de 240 m², una base de longitud 11 m y la otra base de longitud 13 m, encuentra su altura.
Solución
Tenemos lo siguiente:
- Área, $latex A=240$ m²
- Base 1, $latex b_{1}=11$ m
- Base 2, $latex b_{2}=13$ m
Entonces, usamos la fórmula del área de un trapecio y resolvemos para h:
$$A=\frac{(b_{1}+b_{2})h}{2}$$
$$240=\frac{(11+13)h}{2}$$
$latex 480=(11+13)h$
$latex 480=24h$
$latex h=20$
La altura del trapecio mide 20 m.
EJERCICIO 9
Encuentra la longitud de los lados laterales de un trapecio isósceles que tiene un perímetro de 64 cm y la longitud de sus lados paralelos son 13 cm y 17 cm.
Solución
Podemos representar a la longitud de los lados laterales con c. Entonces, reemplazamos los valores dados en la fórmula y resolvemos para c:
$latex p=a+b+2c$
$latex 64=13+17+2c$
$latex 64=30+2c$
$latex 34=2c$
$latex c=17$
La longitud de uno de los lados laterales es 17 cm.
EJERCICIO 10
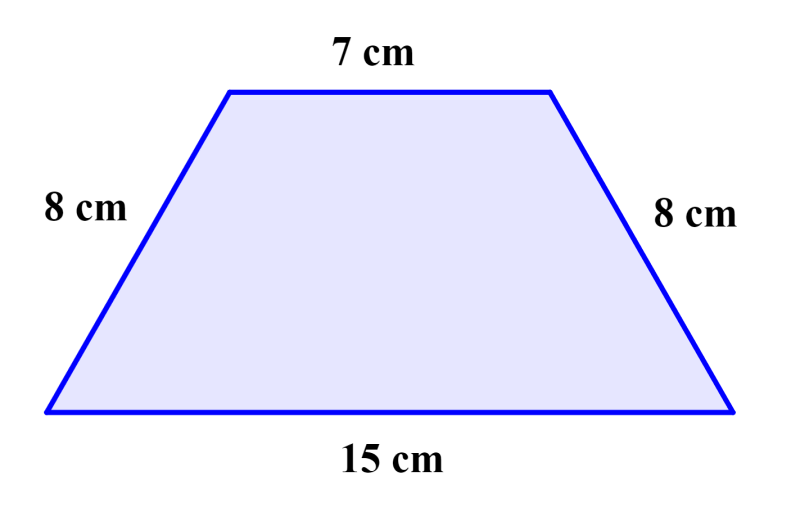
Encuentra el área del siguiente trapecio.
Solución
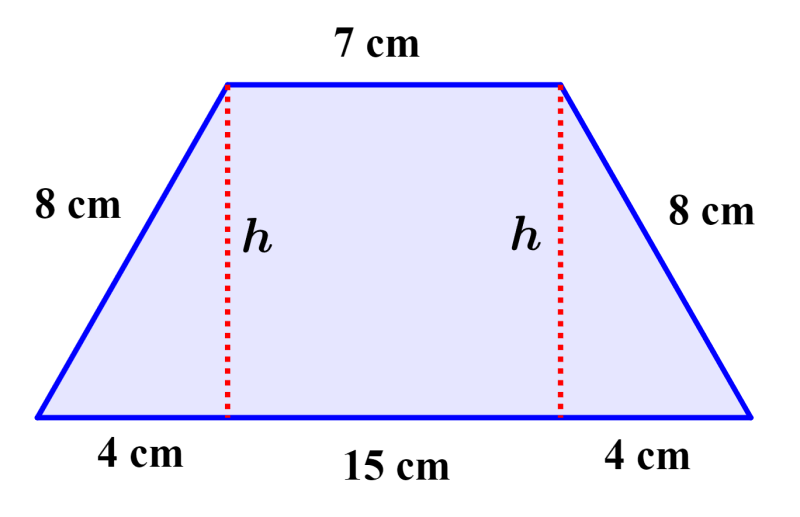
Este es un trapecio isósceles que tiene dos lados laterales iguales. Entonces, vamos a calcular la altura del trapecio como se muestra en el diagrama abajo.
Obtenemos las bases de los dos triángulos al restar 7 de 15 y dividir para 2.
⇒ $latex \frac{15-7}{2}=4$ cm
Usando el teorema de Pitágoras, podemos calcular la altura:
$latex {{8}^2}={{h}^2}+{{4}^2}$
$latex 64={{h}^2}+16$
$latex {{h}^2}=48$
$latex h=6.93$ cm
Ahora, podemos usar la altura y la base para calcular el área del trapecio:
$$A=\frac{(b_{1}+b_{2})h}{2}$$
$$=\frac{(15+7)6.93}{2}$$
$$=\frac{(22)(6.93)}{2}$$
$latex A=76.23$
El área del trapecio es 76.23 cm².
Perímetro y área de un trapecio – Ejercicios para resolver
Véase también
¿Interesado en aprender más sobre perímetro y área de figuras geométricas? Puedes visitar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
