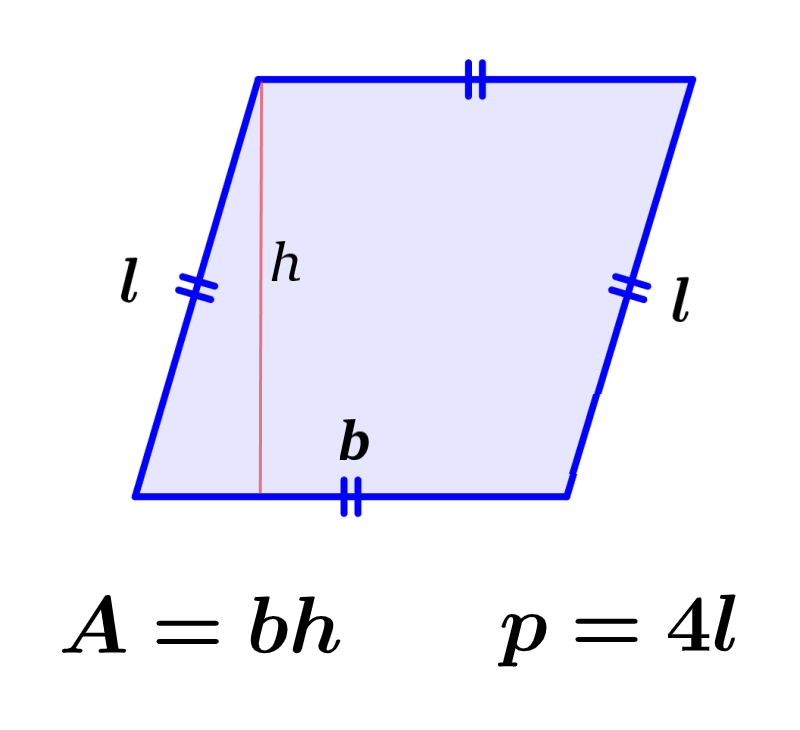
El perímetro de un rombo representa la longitud de su contorno. Por otro lado, el área del rombo es una medida del espacio ocupado por el rombo en el espacio bidimensional. El perímetro de un rombo puede ser calculado usando la fórmula p = 4l, en donde l es la longitud de un lado, y su área puede ser calculada usando la fórmula A = bh, en donde b es la base y h es su altura.
A continuación, aprenderemos todo lo relacionado sobre el perímetro y el área de un rombo. Conoceremos las diferentes fórmulas que podemos usar y las aplicaremos para resolver algunos ejercicios de práctica.
¿Cómo calcular el perímetro de un rombo?
Para calcular el perímetro de un rombo, tenemos que sumar las longitudes de todos sus lados. Dado que un rombo es un cuadrilátero con cuatro lados iguales, la fórmula para el perímetro de un rombo puede ser escrita como:
| $latex p=4l$ |
en donde,
- p es el perímetro del rombo
- l es la longitud de uno de los lados del rombo
Esto significa que para calcular el perímetro de un rombo, solo tenemos que conocer la longitud de uno de sus lados.
¿Cómo calcular el área de un rombo?
El área de un rombo puede ser calculada usando tres métodos diferentes dependiendo en la información que tengamos disponible. Podemos usar sus diagonales, podemos usar su base y altura y podemos usar trigonometría.
Calcular el área del rombo usando diagonales
Podemos calcular el área de un rombo cuando conocemos la longitud de sus diagonales al usar la siguiente fórmula:
| $latex A=\frac{d_{1}\times d_{2}}{2}$ |
en donde,
- $latex d_{1}=$ longitud de la diagonal 1
- $latex d_{2}=$ longitud de la diagonal 2
- $latex A=$ área del rombo
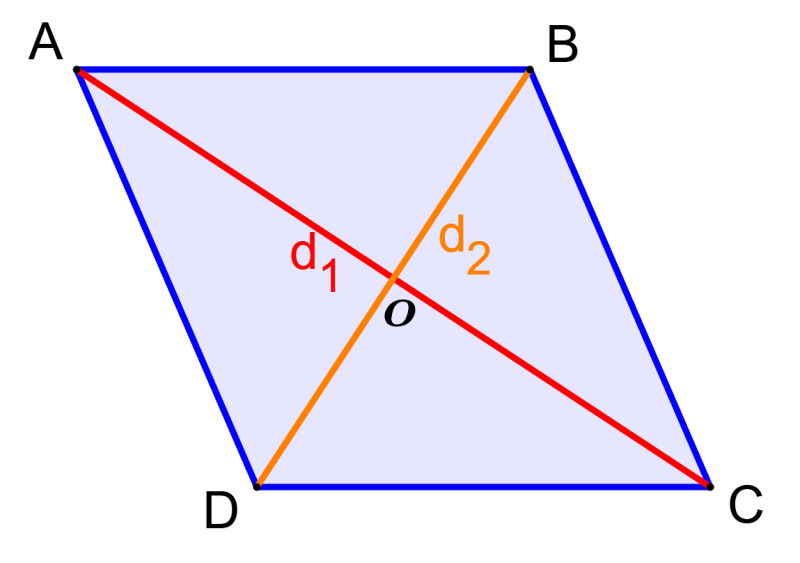
Demostración de la fórmula del área de un rombo
Podemos demostrar la fórmula del área de un rombo usando el siguiente diagrama:
El punto O es el punto de intersección de las dos diagonales del rombo. Entonces, el área del rombo será:
$latex A=4\times\text{área de }\Delta AOB$
$latex =4\times(\frac{1}{2})\times AO \times OB$
$latex =4\times(\frac{1}{2})\times(\frac{1}{2})d_{1}\times(\frac{1}{2})d_{2}$
$latex =4\times(\frac{1}{8})d_{1}d_{2}$
$latex =\frac{1}{2}d_{1}d_{2}$
Calcular el área del rombo usando la base y la altura
Cuando conocemos la longitud de la base y la longitud de la altura del rombo, podemos usar la siguiente fórmula para calcular su área:
| $latex A=bh$ |
en donde,
- $latex b=$ longitud de cualquier lado del rombo
- $latex h=$ longitud de la altura del rombo
- $latex A=$ área del rombo
Calcular el área del rombo usando trigonometría
Podemos usar trigonometría para calcular el área del rombo cuando conocemos la medida de un ángulo del rombo. Entonces, usamos la siguiente fórmula:
| $latex A={{b}^2}\times \sin(a)$ |
en donde,
- $latex b=$ longitud de cualquier lado del rombo
- $latex a=$ medida de cualquier ángulo interno
- $latex A=$ área del rombo
Perímetro y área de un rombo – Ejercicios resueltos
EJERCICIO 1
¿Cuál es el perímetro de un rombo que tiene lados con una longitud de 7 cm?
Solución
Los lados del rombo tienen una longitud de 7 cm. Entonces, usamos esa longitud en la fórmula del perímetro:
$latex p=4l$
$latex p=4(7)$
$latex p=28$
El perímetro del rombo es igual a 28 cm.
EJEMPLO 2
¿Cuál es el área de un rombo que tiene diagonales con longitudes de 8 cm y 10 cm?
Solución
Tenemos las siguientes longitudes
- Diagonal 1, $latex d_{1}=8$ cm
- Diagonal 2, $latex d_{2}=10$ cm
Al usar la fórmula del área con estos valores, tenemos:
$latex A=\frac{d_{1}\times d_{2}}{2}$
$latex =\frac{8\times 10}{2}$
$latex =\frac{80}{2}$
$latex A=40$
Entonces, el área del rombo es igual a 40 cm².
EJERCICIO 3
Determina el perímetro de un rombo que tiene lados con una longitud de 12 mm.
Solución
Usando la fórmula del perímetro con la longitud dada, tenemos:
$latex p=4l$
$latex p=4(12)$
$latex p=48$
El perímetro del rombo es igual a 48 mm.
EJEMPLO 4
Encuentra el área de un rombo que tiene diagonales con longitudes de 10 m y 12 m.
Solución
Tenemos las siguientes longitudes:
- Diagonal 1, $latex d_{1}=10$ m
- Diagonal 2, $latex d_{2}=12$ m
Al usar estas longitudes en la fórmula del área, tenemos:
$latex A=\frac{d_{1}\times d_{2}}{2}$
$latex =\frac{10\times 12}{2}$
$latex =\frac{120}{2}$
$latex A=60$
Entonces, el área del rombo es igual a 60 m².
EJERCICIO 5
Encuentra el perímetro de un rombo que tiene lados con una longitud de 15 mm.
Solución
Aplicamos la fórmula del perímetro con la longitud dada:
$latex p=4l$
$latex p=4(15)$
$latex p=60$
El perímetro del rombo es igual a 60 mm.
EJEMPLO 6
Encuentra el área de un rombo que tiene una base de 8 m y una altura de 6 m.
Solución
Tenemos las siguientes longitudes:
- Base, $latex b=8$ m
- Altura, $latex h=6$ m
Aplicando la fórmula del área con la información conocida, tenemos:
$latex A=bh$
$latex =(8)(6)$
$latex A=48$
Entonces, el área del rombo es igual a 48 m².
EJERCICIO 7
¿Cuál es la longitud de los lados de un rombo que tiene un perímetro igual a 36 m?
Solución
En este ejercicio, conocemos la medida del perímetro y queremos encontrar la longitud de uno de los lados del rombo. Entonces, usamos la fórmula del perímetro y resolvemos para l:
$latex p=4l$
$latex 36=4l$
$latex l=9$
La longitud de un lado del rombo es 9 m.
EJEMPLO 8
Determina el área de un rombo tiene lados con una longitud 10 m y un ángulo interno mide 60°.
Solución
Tenemos la siguiente información
- Lado, $latex b=10$ m
- Ángulo, $latex a=60°$
Usando la fórmula del área de un rombo con esta información, tenemos:
$latex A={{b}^2}\times \sin(60°)$
$latex ={{10}^2}\times 0.866$
$latex =100\times 0.866$
$latex A=866$
Entonces, el área del rombo es igual a 866 m².
EJERCICIO 9
Encuentra la longitud de los lados de un rombo que tiene un perímetro igual a 68 cm.
Solución
Usamos la fórmula del perímetro de un rombo y resolvemos para l:
$latex p=4l$
$latex 68=4l$
$latex l=17$
La longitud de uno de los lados del rombo es 17 cm.
EJERCICIO 10
Encuentra el área de un rombo que tiene una base de 5.5 cm y una altura de 6.5 cm.
Solución
Tenemos lo siguiente:
- Base, $latex b=5.5$ cm
- Altura, $latex h=6.5$ cm
Cuando aplicamos la fórmula del área, tenemos:
$latex A=bh$
$latex =(5.5)(6.5)$
$latex A=35.75$
Entonces, el área del rombo es igual a 35.75 cm².
Perímetro y área de un rombo – Ejercicios para resolver
Véase también
¿Interesado en aprender más sobre perímetro y área de figuras geométricas? Puedes visitar estas páginas: