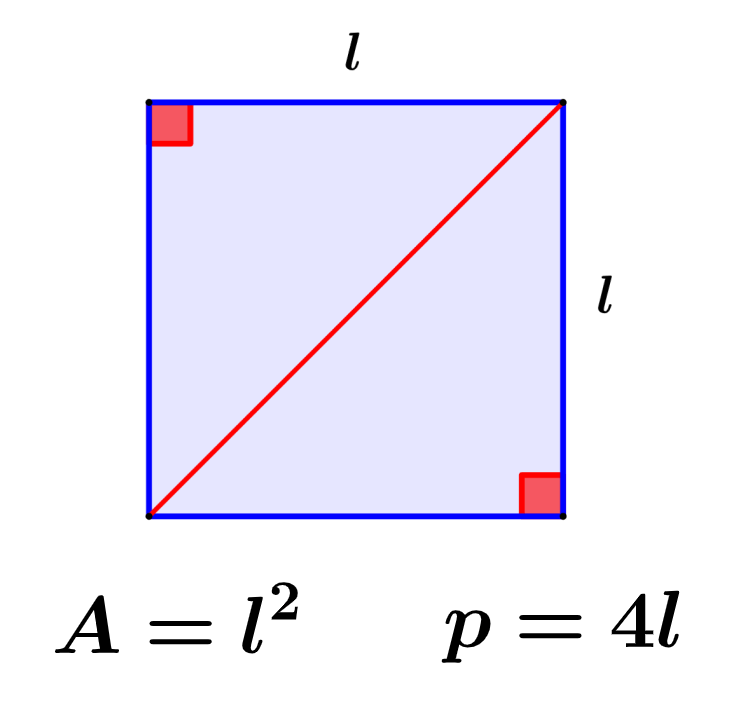El perímetro de un cuadrado representa la suma de las longitudes de todos sus lados. Por otro lado, el área de un cuadrado representa el espacio ocupado por el cuadrado en el espacio bidimensional. Podemos calcular el perímetro de un cuadrado usando la fórmula p = 4l y podemos calcular el área de un cuadrado usando la fórmula A = l2.
A continuación, aprenderemos sobre el perímetro y el área de un cuadrado detalladamente. Conoceremos sus fórmulas y las usaremos para resolver algunos ejercicios de práctica.
¿Cómo calcular el perímetro de un cuadrado?
Para calcular el perímetro de un cuadrado, podemos sumar la longitud de sus cuatro lados. Dado que todos los lados de un cuadrado tienen la misma longitud, la fórmula para calcular el perímetro de un cuadrado es 4 multiplicado por la longitud de un lado:
| Perímetro = 4 × lado $latex p=4l$ |
Demostración de la fórmula del perímetro de un cuadrado
La fórmula del perímetro del cuadrado está dada por:
Perímetro = Suma de los cuatro lados
Perímetro = lado + lado + lado + lado
Perímetro = 4 × lado
Entonces, el perímetro del cuadrado es igual a 4l, en donde l es igual a la longitud de un lado del cuadrado.
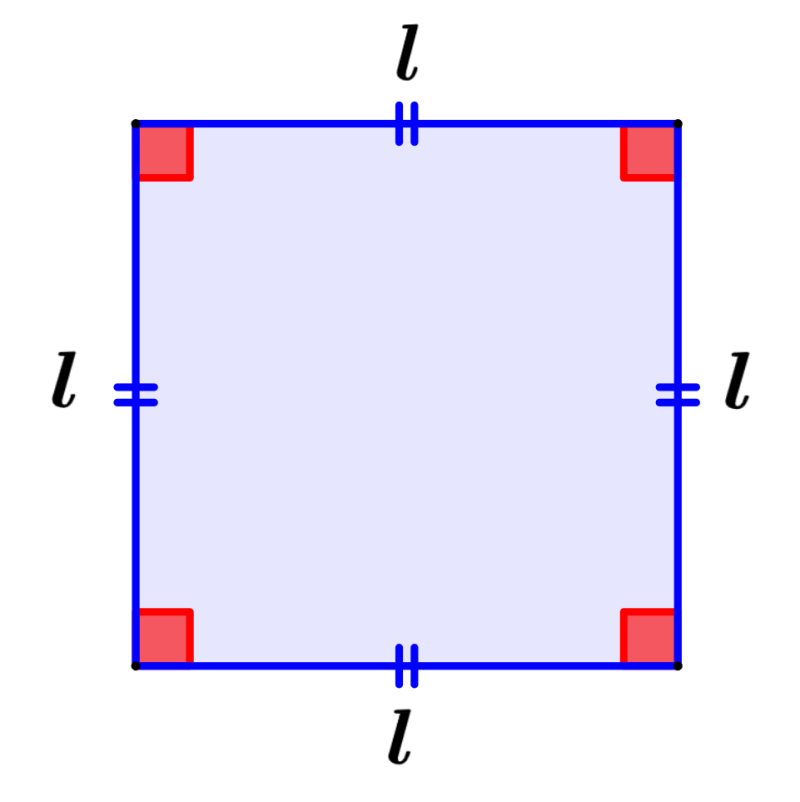
¿Cómo calcular el área de un cuadrado?
Podemos calcular el área de un cuadrado al elevar al cuadrado a la longitud de uno de los lados del cuadrado. Entonces, tenemos la siguiente fórmula:
| $latex A={{l}^2}$ |
en donde,
- A es el área del cuadrado
- l es la longitud de uno de los lados del cuadrado
Demostración de la fórmula del área de un cuadrado
Para demostrar la fórmula del área de un cuadrado, vamos a encontrar el área de un cuadrado que tiene lados de longitud 5 cm como se muestra en el siguiente diagrama.
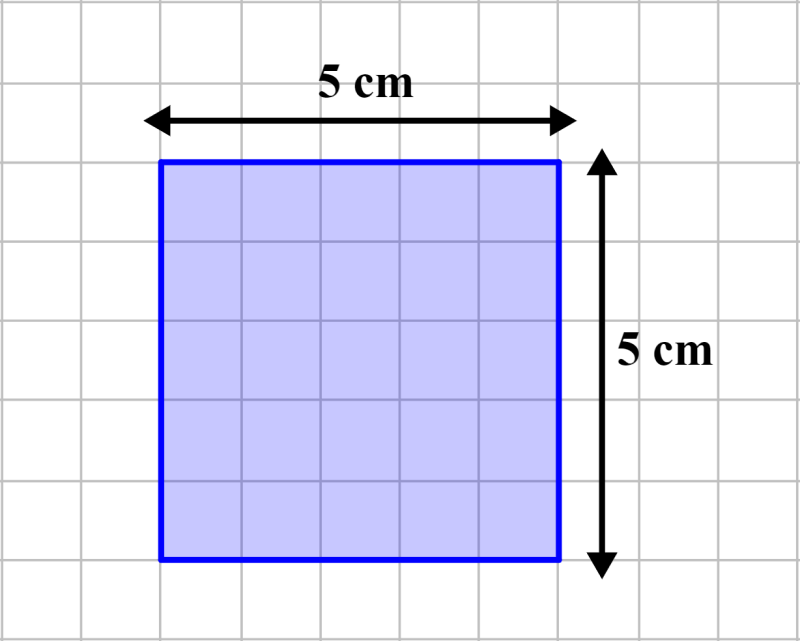
El cuadrado es trazado en una cuadrícula de 1 cm × 1 cm. Entonces, el cuadrado que dibujamos cubre 25 de los cuadrados pequeños.
Esto significa que el área del cuadrado es 25 cm², lo cual puede ser escrito como 5 cm × 5 cm, es decir, tenemos lado × lado. Entonces, tenemos que el área del cuadrado es:
| Área = Lado × Lado Área = Lado² $latex A={{l}^2}$ |
Perímetro y área de un cuadrado – Ejercicios resueltos
EJERCICIO 1
Determina el perímetro de un cuadrado que tiene lados de longitud 8 cm.
Solución
Usamos la fórmula del perímetro de un cuadrado con la longitud l=8:
$latex p=4l$
$latex p=4(8)$
$latex p=32$
Entonces, el perímetro del cuadrado es 32 cm.
EJERCICIO 2
¿Cuál es el área de un cuadrado que tiene lados de longitud de 12 m?
Solución
Usamos la fórmula del área de un cuadrado con la longitud l=12 m.
$latex A={{l}^2}$
$latex A={{12}^2}$
$latex A=144$
Entonces, el área del cuadrado es 144 m².
EJERCICIO 3
Si es que un cuadrado tiene lados con una longitud de 12 cm, ¿cuál es su perímetro?
Solución
Al aplicar la fórmula del perímetro con la longitud l=12, tenemos:
$latex p=4l$
$latex p=4(12)$
$latex p=48$
El perímetro del cuadrado es 48 cm.
EJERCICIO 4
Determina el área de un cuadrado que tiene lados con una longitud de 15 cm.
Solución
La longitud de un lado del cuadrado es 15 cm, por lo que usamos la fórmula del área con este valor:
$latex A={{l}^2}$
$latex A={{15}^2}$
$latex A=225$
Entonces, el área del cuadrado es 225 cm².
EJERCICIO 5
Encuentra el perímetro de un cuadrado que tiene lados con una longitud de 25 mm.
Solución
Usamos el valor l=25 en la fórmula del perímetro y tenemos:
$latex p=4l$
$latex p=4(25)$
$latex p=100$
Entonces, el perímetro del cuadrado es 100 mm.
EJERCICIO 6
Una pared cuadrada tiene lados con una longitud de 6 m. ¿Cuál es el costo de pintar la pared si tenemos una tasa de 0.5 dólares por metro cuadrado?
Solución
Primero, tenemos que encontrar el área de la pared. Entonces, usamos la fórmula $latex A={{l}^2}$ con una longitud l=6:
$latex A={{l}^2}$
$latex A={{6}^2}$
$latex A=36$
El área de la pared es 36 metros cuadrados. Si es que la tasa es 0.5 dólares por metro cuadrado, el costo será:
$latex 36\times 0.5=18$ dólares
EJERCICIO 7
Determina la longitud de los lados de un cuadrado que tiene un perímetro de 44 m.
Solución
Aquí, tenemos el perímetro y queremos determinar la longitud de uno de los lados. Entonces, usamos la fórmula del perímetro y resolvemos para l:
$latex p=4l$
$latex 44=4l$
$latex l=11$
Entonces, la longitud de cada lado del cuadrado es 11 m.
EJERCICIO 8
Encuentra la longitud de uno de los lados de un cuadrado que tiene un área de 121 mm².
Solución
Aquí, conocemos el área y queremos encontrar la longitud de uno de los lados del cuadrado. Entonces, usamos la fórmula del área y resolvemos para l:
$latex A={{l}^2}$
$latex 121={{l}^2}$
$latex l=\sqrt{121}$
$latex l=11$
Entonces, la longitud de un lado del cuadrado es 11 mm.
EJERCICIO 9
¿Cuál es la longitud de los lados de un cuadrado que tiene un perímetro de 60 cm?
Solución
El perímetro del cuadrado es 60 cm. Entonces, usamos la fórmula del perímetro con el valor p=60 y despejamos para l para encontrar la longitud de los lados:
$latex p=4l$
$latex 60=4l$
$latex l=15$
Entonces, la longitud de los lados del cuadrado es 15 cm.
EJERCICIO 10
Un piso cuadrado que tiene lados con una longitud de 40 m va a ser cubierto de cerámica. Si es que cada cerámica tiene lados con una longitud de 2 m, ¿cuántas cerámicas se necesitan para cubrir el piso?
Solución
Tenemos que encontrar tanto el área del piso, como el área de cada cerámica. Entonces, el área del piso es:
$latex A_{p}={{l_{p}}^2}$
$latex A_{p}={{40}^2}$
$latex A_{p}=1600$
El área del piso es 1600 m² y el área de cada cerámica es:
$latex A_{c}={{l_{c}}^2}$
$latex A_{c}={{2}^2}$
$latex A_{c}=4$
El área de cada cerámica es 4 m². Entonces, necesitamos:
$latex \frac{A_{p}}{A_{c}}=\frac{1600}{4}=400$ cerámicas
Perímetro y área de un cuadrado – Ejercicios para resolver
Véase también
¿Interesado en aprender más sobre perímetro y área de figuras geométricas? Puedes visitar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
