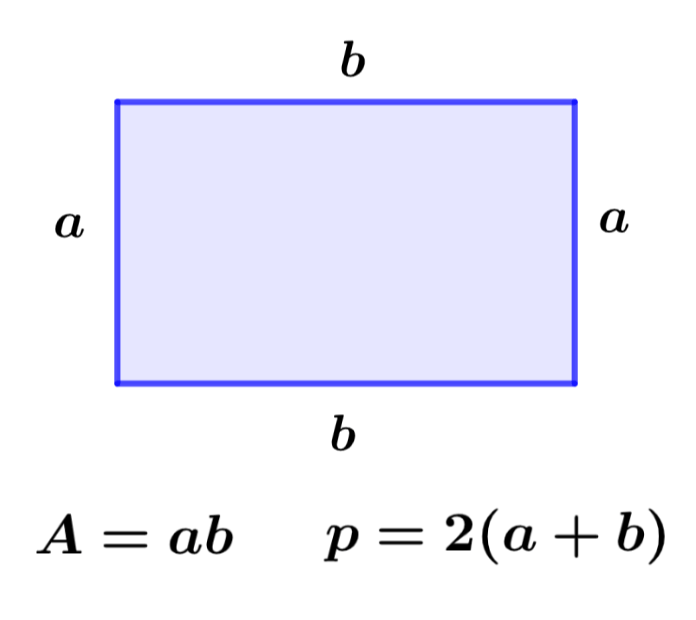
El perímetro de un rectángulo puede ser definido como la longitud del contorno del rectángulo. Por otro lado, el área del rectángulo es una medida del espacio ocupado por el rectángulo en el espacio bidimensional. Podemos calcular el perímetro de un rectángulo usando la fórmula p = 2(a+b) y podemos calcular su área usando la fórmula A = ab, en donde, b es la base del rectángulo y a es su altura.
A continuación, aprenderemos sobre el perímetro y el área de un rectángulo detalladamente. Conoceremos sus fórmulas y las aplicaremos para resolver algunos ejercicios de práctica.
¿Cómo calcular el perímetro de un rectángulo?
El perímetro de un rectángulo puede ser calculado al sumar las longitudes de todos sus lados. Además, en un rectángulo, los lados opuestos son iguales, por lo que el perímetro de un rectángulo es igual al doble de la longitud de la base más el doble de la longitud de la altura del rectángulo.
| Perímetro = 2(Base + Altura) $latex p = 2(a+b)$ |
en donde, a es la altura del triángulo y b es la longitud de su base, como se muestra en el siguiente diagrama:
Demostración de la fórmula del perímetro
El perímetro de cualquier figura geométrica puede ser encontrada al sumar la longitud de todos sus lados. En el caso de un rectángulo, tenemos:
⇒ P = suma de sus cuatro lados
⇒ P = a + b + a + b (lados opuestos son iguales)
⇒ $latex P = 2(a + b)$
¿Cómo calcular el área de un rectángulo?
El área de un rectángulo puede ser calculada multiplicando la longitud de la base del rectángulo por su altura. Entonces, tenemos la siguiente fórmula:
| Área de rectángulo = Base × Altura $latex A=b\times a$ |
El área de un rectángulo es expresada en unidades cuadradas. Entonces, podemos encontrar el área de un rectángulo siguiendo los siguientes pasos:
Paso 1: Identifica las longitudes de la base y de la altura del rectángulo. Asegúrate de que las dimensiones son las mismas. Si la base está dada en metros, la altura también debe estar en metros.
Paso 2: Multiplica las longitudes de la base y de la altura.
Paso 3: Escribe la respuesta en unidades cuadradas.
Demostración de la fórmula del área de un rectángulo
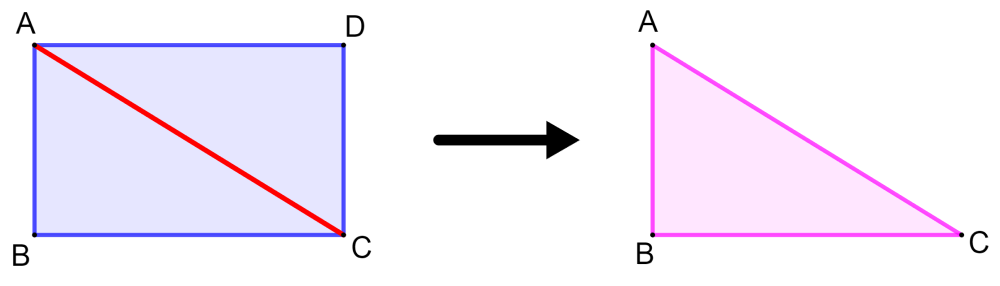
Vamos a usar el siguiente diagrama para demostrar la fórmula del área de un rectángulo:
Tenemos el rectángulo ABCD. La diagonal AC divide al rectángulo en dos triángulos rectángulos, $latex \Delta$ABC y $latex \Delta$ADC. El área del rectángulo es igual a la suma de las áreas de los dos triángulos.
Sabemos que $latex \Delta$ABC y $latex \Delta$ADC son triángulos congruentes, por lo que tenemos:
⇒ Área (ABCD) = Área(ABC) + Área(ADC)
⇒ Área (ABCD) = 2 × Área(ABC)
⇒ Área (ABC) = $latex \frac{1}{2}$ × base × altura
⇒ Área (ABCD) = 2 × ($latex \frac{1}{2}$ × b × h)
⇒ Área (ABCD) = b × h
Perímetro y área de un rectángulo – Ejercicios resueltos
EJERCICIO 1
¿Cuál es el perímetro de un rectángulo que tiene una base de 12 cm y una altura de 5 cm?
Solución
Tenemos las siguientes longitudes:
- Base = 12 cm
- Altura = 5 cm
Usando la fórmula del perímetro, tenemos:
$latex p=2(12+5)$
$latex p=2(17)$
$latex p=34$
Entonces el perímetro del rectángulo es igual a 34 cm.
EJERCICIO 2
Determina el área de un rectángulo que tiene una base de 20 cm y una altura de 12 cm.
Solución
Tenemos las siguientes longitudes:
- Base = 20 cm
- Altura = 12 cm
Para calcular el área, tenemos que multiplicar la longitud de la base por la longitud de la altura:
$latex A=20\times 12=240$
Entonces, el área es 240 cm².
EJERCICIO 3
Si es que un rectángulo tiene una base de 15 mm y una altura de 8 mm, ¿cuál es su perímetro?
Solución
Tenemos lo siguiente:
- Base = 15 m
- Altura = 8 m
Aplicando la fórmula del perímetro, tenemos:
$latex p=2(15+8)$
$latex p=2(23)$
$latex p=46$
El perímetro del rectángulo es igual a 46 mm.
EJERCICIO 4
Una pizarra rectangular tiene las dimensiones 140 cm de base y 90 cm de altura. ¿Cuál es su área?
Solución
Tenemos las siguientes longitudes:
- Base = 140 cm
- Altura = 90 cm
Usando estas longitudes en la fórmula del área, tenemos:
$latex A=140\times 90=12600$
El área de la pizarra es 12 600 cm².
EJERCICIO 5
Un rectángulo tiene un perímetro de 54 cm y su base mide 10 cm. Determina la longitud de su altura.
Solución
Tenemos lo siguiente:
- Perímetro = 54 cm
- Base = 10 cm
En este caso, tenemos el perímetro y queremos determina la longitud de la altura. Entonces, usamos la fórmula del perímetro y resolvemos para a:
$latex p=2(b+a)$
$latex 54=2(10+a)$
$latex 54=20+2a$
$latex 2a=34$
$latex a=17$
La longitud de la altura del rectángulo es igual a 17 cm.
EJERCICIO 6
Un rectángulo tiene un área igual a 120 cm². Si es que su base mide 20 cm, ¿cuál es la longitud de su altura?
Solución
Tenemos la siguiente información:
- Base = 20 cm
- Área = 120 cm²
Podemos usar la fórmula del área y resolver para la altura:
altura $latex =\frac{120}{20}=6$
Entonces, la altura es 6 cm.
EJERCICIO 7
Si es que un rectángulo tiene una base de 18 mm y una altura de 12 mm, ¿cuál es su perímetro?
Solución
Tenemos las siguientes longitudes:
- Base = 18 mm
- Altura = 12 mm
Usando la fórmula del perímetro, tenemos:
$latex p=2(18+12)$
$latex p=2(30)$
$latex p=60$
El perímetro del rectángulo es igual a 60 mm.
EJERCICIO 8
Determina el área de un cuadrado que tiene lados de longitud 8 m.
Solución
Un cuadrado es un caso especial de un rectángulo, en el cual su altura es igual a su base. Entonces, tenemos:
- Base = 8 m
- Altura = 8 m
Usando la fórmula del área de un rectángulo, tenemos:
$latex A=8\times 8=64$
Entonces, el área del cuadrado es 64 m².
EJERCICIO 9
¿Cuál es la longitud de la base de un rectángulo que tiene una altura de 8 y un perímetro de 46?
Solución
Tenemos lo siguiente:
- Altura = 8 m
- Perímetro = 46 m
Usamos la fórmula del perímetro y resolvemos para la base:
$latex p=2(b+a)$
$latex 46=2(b+8)$
$latex 46=2b+16$
$latex 2b=30$
$latex b=15$
La base del rectángulo tiene una longitud de 15 m.
EJERCICIO 10
El área de un cuadrado es igual a 6400 cm². ¿Cuál es la longitud de uno de sus lados?
Solución
Tenemos lo siguiente:
- Área = 6400 cm²
En un cuadrado, la base y la altura tienen la misma longitud, por lo que podemos usar la fórmula A = lado². Entonces, reemplazamos para obtener:
lado $latex =\sqrt{8100}=80$
Entonces, la longitud de uno de los lados es 80 cm.
Perímetro y área de un rectángulo – Ejercicios para resolver
Véase también
¿Interesado en aprender más sobre perímetro y área de figuras geométricas? Puedes visitar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
