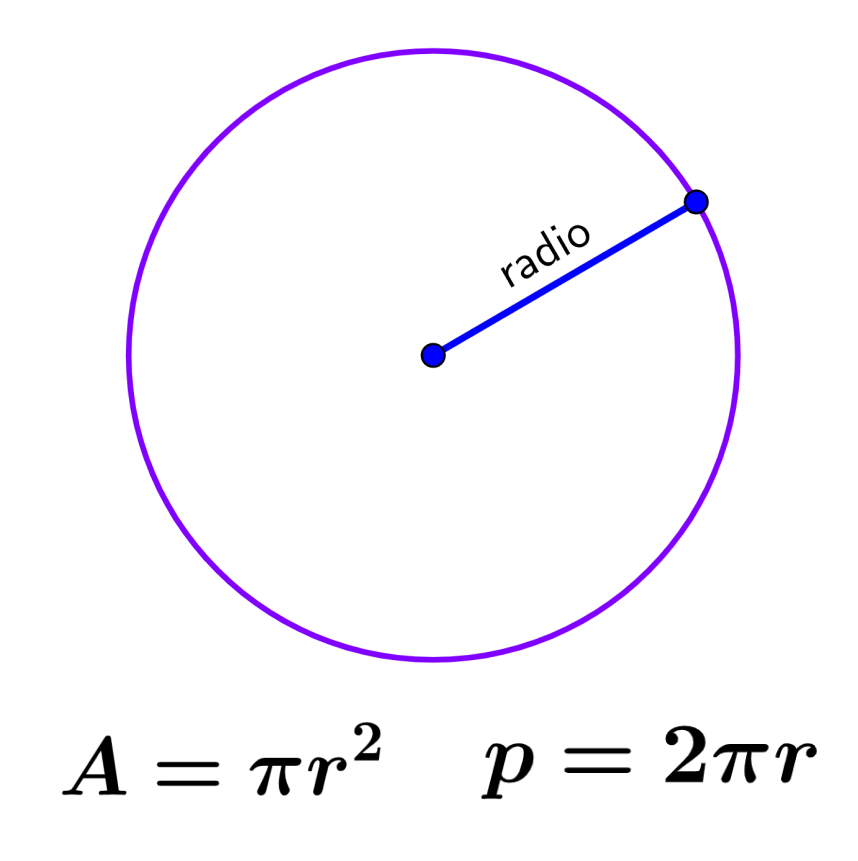El perímetro de un círculo representa a la longitud del contorno del círculo, es decir, el perímetro es igual a la circunferencia. Por otra parte, el área es una medida de la región ocupada por el círculo en el plano bidimensional. El perímetro de un círculo puede ser calculado usando la fórmula C = 2πr y el área puede ser calculada usando la fórmula A = πr², en donde, r es el radio del círculo.
A continuación, aprenderemos sobre el perímetro y el área de un círculo detalladamente. Conoceremos sus fórmulas y las aplicaremos para resolver algunos ejercicios de práctica.
GEOMETRÍA
Relevante para…
Aprender sobre el perímetro y el área de un círculo con ejercicios.
GEOMETRÍA
Relevante para…
Aprender sobre el perímetro y el área de un círculo con ejercicios.
¿Cómo calcular el perímetro de un círculo?
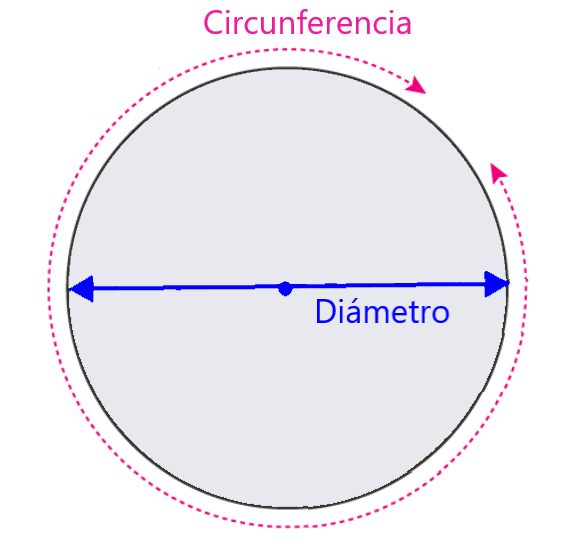
Podemos calcular el perímetro de un círculo, también conocido como la circunferencia, multiplicando a la longitud de su diámetro por la constante pi. Entonces, tenemos la siguiente fórmula:
| $latex C=\pi d$ |
Aquí, d es la longitud del diámetro y π es una constante matemática con un valor aproximado de 3.141592…
Para entender la definición de π, podemos considerar al siguiente círculo:
Como ya mencionamos, el perímetro es igual a la circunferencia, ya que es la longitud del contorno del círculo. Además, vemos que el diámetro es la distancia que cruza al círculo y pasa por el centro. La constante π es la proporción de la circunferencia con respecto al diámetro.
Entonces, la definición de π es la siguiente:
$latex \frac{C}{d}=\pi$
Al reorganizar la fórmula, tenemos la fórmula de la circunferencia o perímetro del círculo:
$latex C=\pi d$
Calcular el perímetro de un círculo con el radio
Para calcular el perímetro de un círculo usando el radio, consideramos que el diámetro es igual a 2r. Entonces, podemos reescribir a la fórmula del perímetro de la siguiete manera:
| $latex C=2\pi r$ |
¿Cómo calcular el área de un círculo?
Para calcular el área de un círculo, podemos multiplicar a π por el radio del círculo elevado al cuadrado. Entonces, tenemos la siguiente fórmula:
| $latex A=πr^2$ |
Recordemos que el radio de un círculo es el segmento que une al centro del círculo con la circunferencia. El siguiente es un círculo con un radio r:
Demostración de la fórmula del área de un círculo
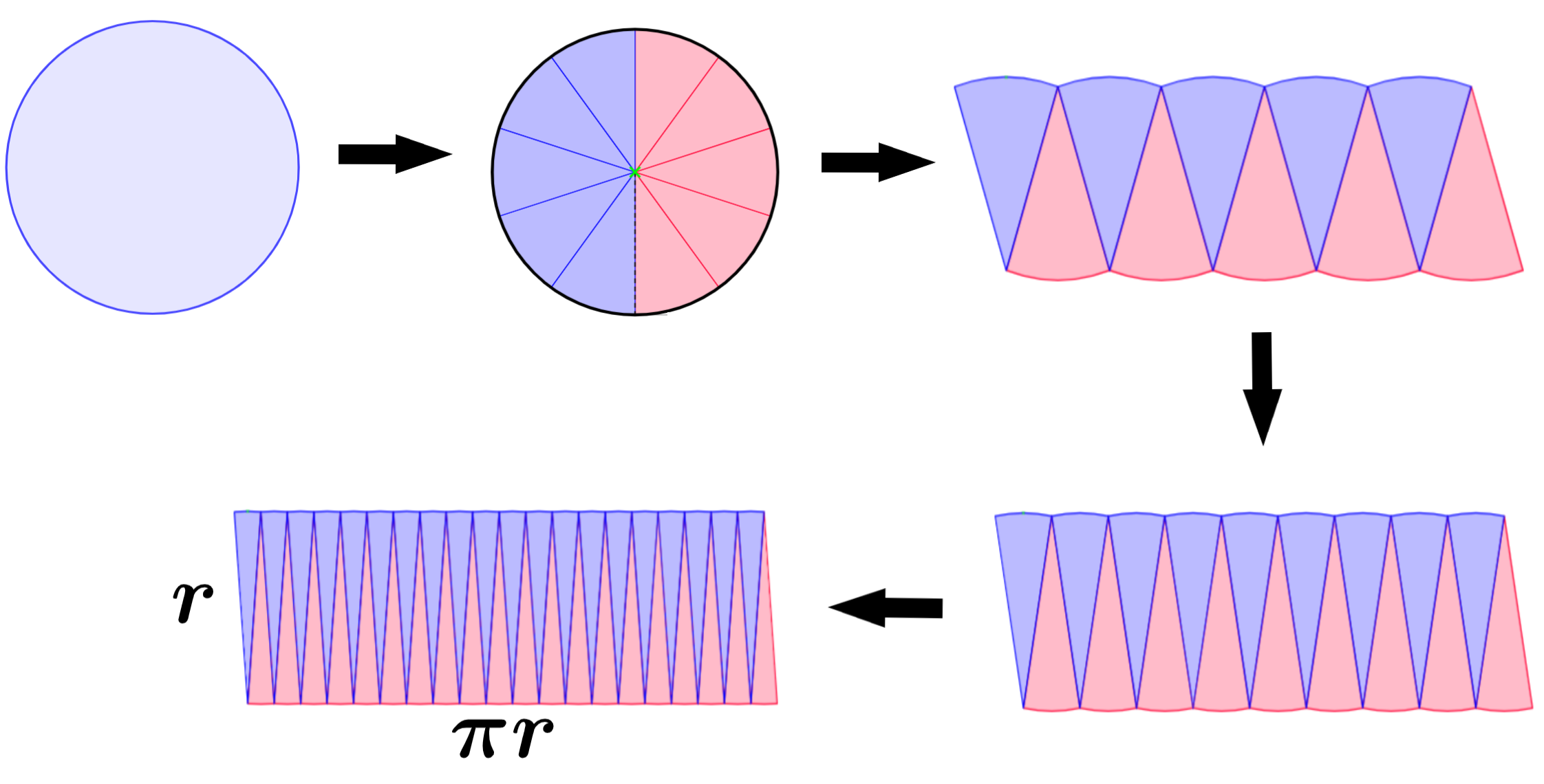
La fórmula del área de un círculo puede ser demostrada usando varias técnicas. Algunas de las técnicas más avanzadas incluyen el uso de Cálculo. Sin embargo, aquí vamos a simplificar un poco la demostración al usar el siguiente diagrama:
Si es que cortamos al círculo en varios sectores, podemos reorganizar los sectores y formar una figura con forma de paralelogramo. Si es que realizamos cortes lo suficientemente pequeños, eventualmente formaremos un paralelogramo.
Si es que el número de sectores cortados del círculo es incrementado, el paralelogramo eventualmente se verá como un rectángulo con una base igual a πr y una altura igual a r.
Dado que el área de un rectángulo es igual a la longitud de su base multiplicada por su altura, tenemos:
$latex A=\pi r\times r$
$latex A=\pi {{r}^2}$
Calcular el área de un círculo usando el diámetro
Para calcular el área de un círculo usando el diámetro, recordamos que el diámetro es igual a 2r. Equivalentemente, podemos escribir $latex r=\frac{d}{2}$. Entonces, usamos esta equivalencia en la fórmula del área de un círculo:
$latex A=\pi {{r}^2}$
$latex A=\pi {{(\frac{d}{2})}^2}$
| $latex A=\pi (\frac{{{d}^2}}{4})$ |
en donde, d es la longitud del diámetro
Perímetro y área de un círculo – Ejercicios resueltos
Las fórmulas del perímetro y del área de un círculo son usadas para resolver los siguientes ejercicios. Intenta resolver los ejercicios tú mismo antes de mirar la solución.
EJERCICIO 1
Determina el perímetro de un círculo que tiene un diámetro de 6 metros.
Solución
Usamos el valor $latex d=6$ en la fórmula del perímetro con respecto al diámetro:
$latex C=\pi d$
$latex C=\pi (6)$
$latex C=18.8$
El perímetro del círculo es igual a 18.8 m.
EJERCICIO 2
Si es que un círculo tiene un radio de 5 cm, ¿cuál es su área?
Solución
Vamos a usar la fórmula del área con respecto al radio con el valor $latex r=5$. Entonces, tenemos:
$latex A=\pi {{r}^2}$
$latex A=\pi {{(5)}^2}$
$latex A=\pi (25)$
$latex A=78.5$
El área del círculo es 78.5 cm².
EJERCICIO 3
Encuentra el perímetro de un círculo que tiene un diámetro de 15 cm.
Solución
Aplicamos la fórmula del perímetro de un círculo con el valor $latex d=15$:
$latex C=\pi d$
$latex C=\pi (15)$
$latex C=47.1$
El perímetro es igual a 47.1 cm.
EJERCICIO 4
Encuentra el área de un círculo que tiene un radio de 12 mm.
Solución
Usando la fórmula del área de un círculo con el valor $latex r=12$, tenemos:
$latex A=\pi {{r}^2}$
$latex A=\pi {{(12)}^2}$
$latex A=\pi (144)$
$latex A=452.4$
El área del círculo es 452.4 mm².
EJERCICIO 5
Encuentra la longitud del perímetro de un círculo que tiene un radio de 8 m.
Solución
Aquí, tenemos la longitud del radio en vez del diámetro, por lo que usamos el valor $latex r=8$ en la siguiente fórmula:
$latex C=2\pi r$
$latex C=2\pi (8)$
$latex C=50.3$
El perímetro es igual a 50.3 m.
EJERCICIO 6
Determina el área de un círculo que tiene un diámetro de 10 m.
Solución
Usamos la fórmula del área de un círculo en términos del diámetro con el valor $latex d=10$:
$latex A=\pi(\frac{{{d}^2}}{4})$
$latex A=\pi(\frac{{{(10)}^2}}{4})$
$latex A=\pi(\frac{100}{4})$
$latex A=\pi(25)$
$latex A=78.5$
El área del círculo es 78.5 m².
EJERCICIO 7
Encuentra el perímetro de un círculo que tiene un radio de 13 mm.
Solución
Usamos el valor $latex r=13$ en la fórmula del perímetro de un círculo. Entonces, tenemos:
$latex C=2\pi r$
$latex C=2\pi (13)$
$latex C=81.7$
El perímetro es igual a 81.7 mm.
EJERCICIO 8
¿Cuál es el área un círculo tiene un diámetro de 20 cm?
Solución
Vamos a usar la fórmula del área de un círculo en términos del diámetro. Entonces, reemplazamos el valor $latex d=20$:
$latex A=\pi(\frac{{{d}^2}}{4})$
$latex A=\pi(\frac{{{(20)}^2}}{4})$
$latex A=\pi(\frac{400}{4})$
$latex A=\pi(100)$
$latex A=314.16$
El área del círculo es 314.16 cm².
EJERCICIO 9
¿Cuál es el diámetro de un círculo que tiene un perímetro de 100 mm?
Solución
En este ejercicio, conocemos el perímetro del círculo y vamos a encontrar el diámetro, por lo que usamos el valor $latex C=100$ en la fórmula y resolvemos para d:
$latex C=\pi d$
$latex 100=\pi d$
$latex d=\frac{100}{\pi}$
$latex d=31.8$
La longitud del diámetro es igual a 31.8 mm.
EJERCICIO 10
Encuentra la longitud del radio de un círculo que tiene un área de 150 cm².
Solución
En este ejercicio, conocemos el área y vamos a encontrar la longitud del radio. Entonces, usamos el valor $latex A=150$ en la fórmula del área y resolvemos para r:
$latex A=\pi {{r}^2}$
$latex 150=\pi {{r}^2}$
$latex {{r}^2}=\frac{150}{\pi}$
$latex {{r}^2}=47.75$
$latex r=6.91$
El radio del círculo es 6.91 cm.
Perímetro y área de un círculo – Ejercicios para resolver
Resuelve los siguientes ejercicios usando lo aprendido sobre el perímetro y el área de un círculo. Haz clic en «Verificar» para comprobar que obtuviste la respuesta correcta.
Véase también
¿Interesado en aprender más sobre perímetro y área de figuras geométricas? Puedes visitar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
