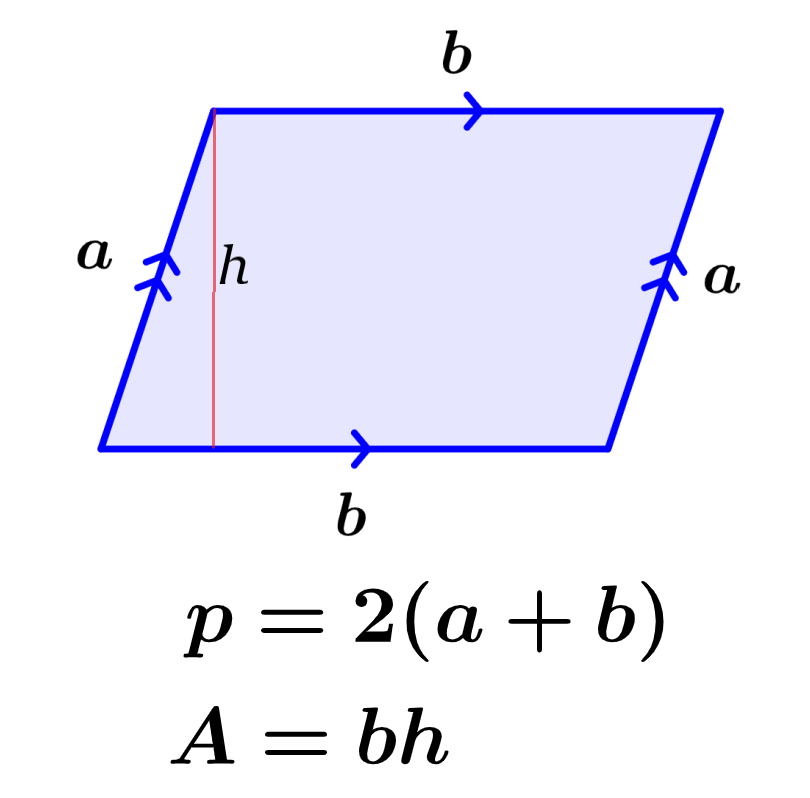
El perímetro de un paralelogramo representa la longitud del contorno del paralelogramo. Por otro lado, el área es una medida del espacio bidimensional ocupado por la figura. Podemos encontrar el perímetro del paralelogramo al sumar las longitudes de sus cuatro lados y podemos calcular el área al multiplicar la longitud de su base por su altura.
A continuación, aprenderemos todo lo relacionado sobre el perímetro y el área de un paralelogramo. Conoceremos sus fórmulas y las aplicaremos para resolver algunos ejercicios de práctica.
¿Cómo calcular el perímetro de un paralelogramo?
Para calcular el perímetro de un paralelogramo, tenemos que sumar las longitudes de todos sus lados. Considerando que los lados opuestos de un paralelogramo tienen la misma longitud, podemos formar la siguiente fórmula:
$latex p=a+b+a+b$
$latex p=2a+2b$
| $latex p=2(a+b)$ |
Calcular el perímetro de un paralelogramo con base y altura
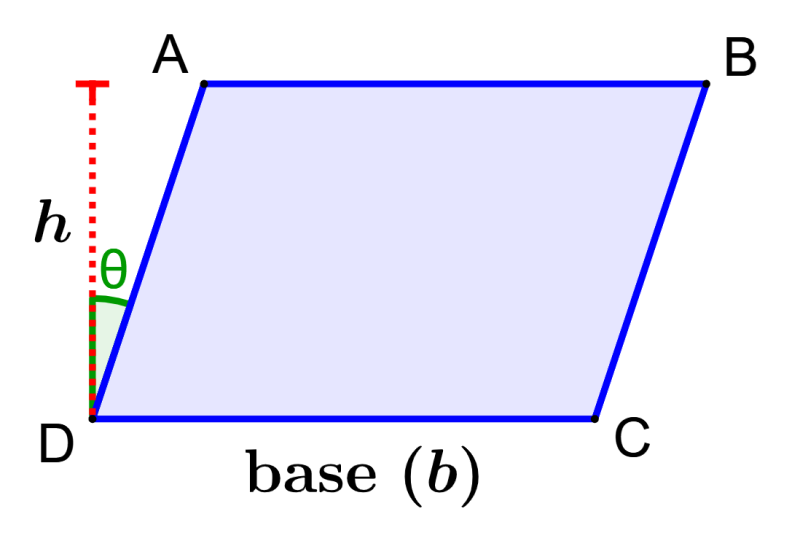
Para calcular el perímetro de un paralelogramo usando su base y su altura, necesitamos el ángulo entre su altura y su lado lateral, como se muestra en el siguiente diagrama.
En un paralelogramo, los lados opuestos son paralelos e iguales y el perímetro del paralelogramo es definido como el doble del producto de la base y la altura multiplicada por el coseno del ángulo:
| $latex p=2(b+h~\cos(\theta))$ |
en donde, $latex \theta$ es el ángulo formado entre la altura y el lado lateral del paralelogramo.
¿Cómo calcular el área de un paralelogramo?
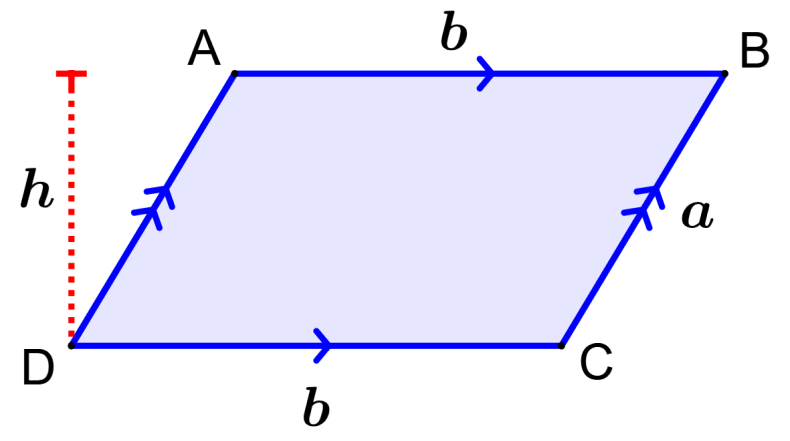
Para calcular el área de un paralelogramo, podemos multiplicar la longitud de la base por su altura. Debemos considerar que la base y la altura del paralelogramo son perpendiculares la una con la otra, mientras que el lado lateral del paralelogramo no es perpendicular a la base.
Por ejemplo, en el siguiente diagrama, podemos observar que la altura del paralelogramo es diferente de su lado lateral:
Entonces, podemos usar la siguiente fórmula para encontrar el área de un paralelogramo:
| $latex A=bh$ |
en donde, b es la longitud de la base y h es la altura.
Calcular el área de un paralelogramo sin usar la altura
Podemos calcular el área de un paralelogramo sin su altura si es que conocemos las longitudes de sus lados y el ángulo entre sus lados. Entonces, usamos la siguiente fórmula:
| $latex A=ab\sin(x)$ |
en donde, a y b son las longitudes de los lados del paralelogramo y x es la medida del ángulo entre los lados.
Calcular el área de un paralelogramo usando diagonales
Podemos calcular el área de un paralelogramo cuando conocemos las longitudes de las diagonales y el ángulo de intersección de las diagonales. Entonces, usamos la siguiente fórmula:
| $latex A=\frac{d_{1}\times d_{2}\sin(y)}{2}$ |
en donde, $latex d_{1}, ~d_{2}$ son las longitudes de las diagonales y y es el ángulo de intersección de las diagonales.
Perímetro y área de un paralelogramo – Ejercicios resueltos
EJERCICIO 1
Encuentra el perímetro de un paralelogramo que tiene lados de longitud 8 mm y 12 mm.
Solución
Tenemos las siguientes longitudes:
- Lado 1, $latex a=8$ mm
- Lado 2, $latex b=12$ mm
Al aplicar la fórmula del perímetro con estos valores, tenemos:
$latex p=2(a+b)$
$latex p=2(8+12)$
$latex p=2(20)$
$latex p=40$
El perímetro del paralelogramo es igual a 40 mm.
EJERCICIO 2
Encuentra el área de un paralelogramo que tiene bases de longitud 12 m y una altura de 11 m.
Solución
Tenemos lo siguiente:
- Base, $latex b=12$m
- Altura, $latex h=11$ m
Al usar la fórmula del área con estas longitudes, tenemos:
$latex A=bh$
$latex A=(12)(11)$
$latex A=132$
El área del paralelogramo es 132 m².
EJERCICIO 3
Calcula el perímetro de un paralelogramo que tiene lados de longitud 15 cm y 17 cm.
Solución
Tenemos lo siguiente:
- Lado 1, $latex a=15$ cm
- Lado 2, $latex b=17$ cm
Al usar la fórmula del perímetro con estos valores, tenemos:
$latex p=2(a+b)$
$latex p=2(15+17)$
$latex p=2(32)$
$latex p=64$
El perímetro del paralelogramo es igual a 64 cm.
EJERCICIO 4
Encuentra el área de un paralelogramo que tiene una base de 15 mm y una altura de 20 mm.
Solución
Tenemos las siguientes longitudes:
- Base, $latex b=15$ mm
- Altura, $latex h=20$ mm
Usando la fórmula del área con estas longitudes, tenemos:
$latex A=bh$
$latex A=(15)(20)$
$latex A=300$
El área del paralelogramo es igual a 300 mm².
EJERCICIO 5
Si es que el perímetro de un paralelogramo es igual a 90 cm y un lado mide 21 cm, ¿cuánto mide el otro lado?
Solución
Tenemos lo siguiente:
- Perímetro, $latex p=90$ cm
- Lado 1, $latex a=21$ cm
En este caso, conocemos el perímetro y queremos encontrar la longitud del otro lado del paralelogramo. Entonces, usamos la fórmula del perímetro y resolvemos para el lado faltante:
$latex p=2(a+b)$
$latex 90=2(21+b)$
$latex 90=42+2b$
$latex 2b=48$
$latex b=24$
La longitud del otro lado es igual a 24 cm.
EJERCICIO 6
¿Cuál es el área de un paralelogramo que tiene lados de longitudes 14 m y 12 m y el ángulo entre ellos es 60°?
Solución
Tenemos lo siguiente:
- Lado 1, $latex a=14$ m
- Lado 2, $latex b=12$ m
- Ángulo, $latex x=60°$
Al usar la segunda fórmula del área de un paralelogramo, tenemos:
$latex A=ab\sin(x)$
$latex A=(14)(12)\sin(60°)$
$latex A=(168)(0.866)$
$latex A=145.5$
El área del paralelogramo es 145.5 m².
EJERCICIO 7
Encuentra el perímetro de un paralelogramo que tiene una altura de 10 m y una base de 12 m si es que el ángulo entre la altura y el lado lateral es 60°.
Solución
Tenemos lo siguiente:
- Altura, $latex h=10$ m
- Base, $latex b=12$ m
- Ángulo, $latex \theta=60°$
Usamos la segunda fórmula del perímetro y tenemos:
$latex p=2(b+h~\cos(\theta))$
$latex p=2(12+10~\cos(60°))$
$latex p=2(12+10(0.5))$
$latex p=2(12+5)$
$latex p=2(17)$
$latex p=34$
El perímetro del paralelogramo es igual a 34 m.
EJERCICIO 8
Un paralelogramo tiene diagonales con longitudes 10 mm y 9 mm. Si es que el ángulo de intersección de las diagonales es 30°, ¿cuál es su área?
Solución
Tenemos lo siguiente:
- Diagonal 1, $latex d_{1}=10$ mm
- Diagonal 2, $latex d_{2}=9$ mm
- Ángulo, $latex y=30°$
Usando la tercera fórmula del área con la información dada, tenemos:
$$A=\frac{d_{1}\times d_{2}\sin(y)}{2}$$
$$A=\frac{10\times 9\sin(30°)}{2}$$
$$A=\frac{(90)(0.5)}{2}$$
$$A=\frac{45}{2}$$
$latex A=22.5$
El área del paralelogramo es igual a 22.5 mm².
EJERCICIO 9
Encuentra el perímetro de un paralelogramo que tiene una altura de 20 cm y un base de 15 cm si es que el ángulo entre la altura y el lado lateral es 60°.
Solución
Tenemos lo siguiente:
- Altura, $latex h=20$ cm
- Base, $latex b=15$ cm
- Ángulo, $latex \theta=60°$
Usamos estos valores en la segunda fórmula del perímetro y tenemos:
$latex p=2(b+h~\cos(\theta))$
$latex p=2(15+20~\cos(60°))$
$latex p=2(15+20(0.5))$
$latex p=2(15+10)$
$latex p=2(25)$
$latex p=50$
El perímetro del paralelogramo es igual a 50 cm.
EJERCICIO 10
El área de un paralelogramo es igual a 182 mm². Si es que su altura mide 13 mm, ¿cuál es la longitud de su base?
Solución
Tenemos los siguientes valores:
- Área, $latex A=182$ mm²
- Altura, $latex h=13$ mm
Usamos la fórmula del área con la información dada y resolvemos para la base, b:
$latex A=bh$
$latex 182=13b$
$latex b=14$
La longitud de la base es 14 mm.
Perímetro y área de un paralelogramo – Ejercicios para resolver
Véase también
¿Interesado en aprender más sobre perímetros y áreas de figuras geométricas? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
