La ley de los senos indica que la proporción de los lados de un triángulo y la proporción de los senos de los ángulos respectivos son equivalentes el uno con el otro. La ley de senos es usada para encontrar un ángulo desconocido o un lado de un triángulo que no es un triángulo rectángulo. La ley de los senos relaciona a por lo menos dos ángulos y las medidas de sus lados respectivos.
A continuación, conoceremos la fórmula de la ley de senos. Aprenderemos a derivar esta fórmula y la aplicaremos para resolver algunos ejercicios de práctica.
Fórmula de la ley de senos
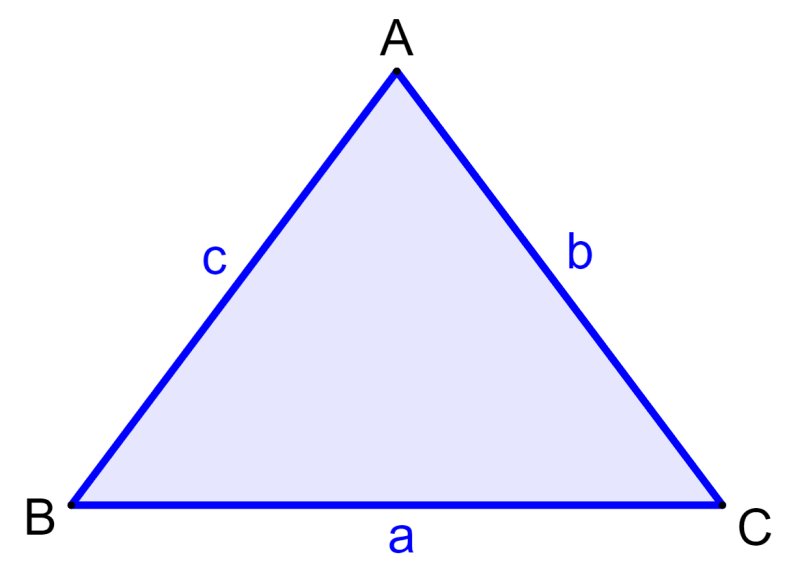
La fórmula de la ley de senos relaciona a las proporciones de los lados de un triángulo con los senos de sus ángulos correspondientes. Entonces, tenemos:
| $latex \frac{a}{\sin(A)}=\frac{b}{\sin(B)}=\frac{c}{\sin(C)}$ |
Aquí, a, b, c son las longitudes de los lados del triángulo y A, B, C son los ángulos del triángulo. Cada lado del triángulo está denotado con respecto a su ángulo opuesto. Por ejemplo, a es el lado opuesto al ángulo A, b es el lado opuesto al ángulo B y c es el lado opuesto al ángulo C.
¿Cuándo se aplica la ley de los senos?
Las funciones trigonométricas como seno, coseno y tangente son funciones principales que son usadas para encontrar ángulos o lados desconocidos de un triángulo. La ley de los senos se aplica en las siguientes situaciones:
- Puede ser usada para calcular el otro lado de un triángulo cuando conocemos la medida de dos ángulos y la longitud de un lado.
- Puede ser usada para calcular un ángulo cuando conocemos la medida de dos lados y un ángulo.
Con la ley de los senos, relacionamos a los ángulos con sus lados opuestos. Entonces, usando el siguiente triángulo, podemos aplicar la ley de los senos si es que conocemos la medida de los ángulos A, B y la longitud del lado a y queremos encontrar la longitud del lado b. También, podemos encontrar la medida del ángulo A si es que conocemos las longitudes de los lados a, b y la medida del ángulo B.
¿Cómo demostrar la ley de los senos?
Podemos demostrar la ley de los senos usando los siguientes dos triángulos:
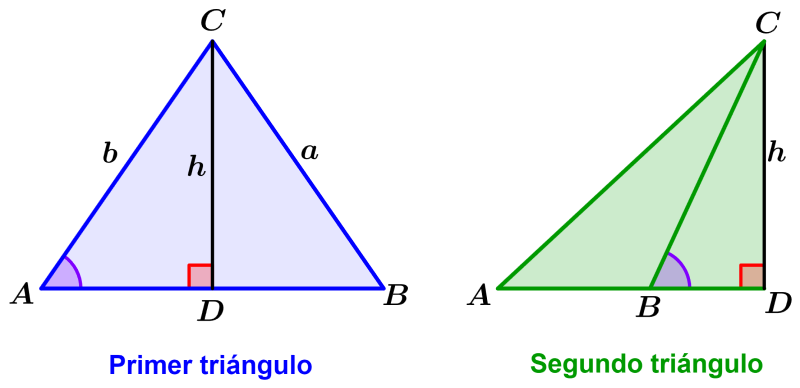
Recordemos que el seno de un ángulo en un triángulo es igual al lado opuesto dividido por la hipotenusa. Entonces, en el primer triángulo, tenemos:
$latex \frac{h}{b}=\sin(A)$
$latex h=b~\sin(A)$
De igual forma, en el segundo triángulo, tenemos:
$latex \frac{h}{a}=\sin(B)$
$latex h=a~\sin(B)$
Obtuvimos dos expresiones para h. Si es que igualamos a ambas expresiones, tenemos:
$latex a~\sin(B)=b~\sin(A)$
$latex \frac{a}{\sin(A)}=\frac{b}{\sin(B)}$
Siguiendo el mismo proceso, podemos derivar una relación para $latex \sin(A)$ y $latex \sin(C)$. Entonces, tenemos:
$latex a~\sin(C)=c~\sin(A)$
$latex \frac{a}{\sin(A)}=\frac{c}{\sin(C)}$
Al combinar las dos expresiones obtenidas, tenemos la ley de los senos:
$latex \frac{a}{\sin(A)}=\frac{b}{\sin(B)}=\frac{c}{\sin(C)}$
Ejercicios de ley de senos resueltos
La fórmula de la ley de los senos es usada para resolver los siguientes ejercicios. Cada uno de los ejercicios tiene su respectiva solución, pero es recomendable que intentes resolver los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
Si es que tenemos los ángulos A=30° y B=40° y tenemos al lado a=10, ¿cuál es la longitud del lado b?
Solución
Empezamos reconociendo la información que tenemos:
- A=30°
- B=40°
- a=10
Usamos la ley de los senos y resolvemos para b:
$latex \frac{a}{\sin(A)}=\frac{b}{\sin(B)}$
$latex \frac{10}{\sin(30)}=\frac{b}{\sin(40)}$
$latex \frac{10}{0.5}=\frac{b}{0.643}$
$latex 5=\frac{b}{0.643}$
$latex b=5(0.643)$
$latex b=3.2$
La longitud de b es 3.2.
EJERCICIO 2
Tenemos los ángulos B=50° y C=35°. Si es que la longitud de b es 8, ¿cuál es la longitud de c?
Solución
Tenemos lo siguiente:
- B=50°
- C=35°
- b=8
Usando estos valores en la fórmula dada, tenemos:
$latex \frac{b}{\sin(B)}=\frac{c}{\sin(C)}$
$latex \frac{8}{\sin(50)}=\frac{c}{\sin(35)}$
$latex \frac{10}{0.766}=\frac{c}{0.574}$
$latex 13.05=\frac{c}{0.574}$
$latex c=13.05(0.574)$
$latex c=7.75$
La longitud de c es 7.75.
EJERCICIO 3
¿Cuál es el valor de A si es que tenemos a=8, B=30° y b=7?
Solución
En este caso, tenemos dos ángulos y un lado:
- a=8
- B=30°
- b=7
Usamos la fórmula dada con estos valores:
$latex \frac{a}{\sin(A)}=\frac{b}{\sin(B)}$
$latex \frac{8}{\sin(A)}=\frac{7}{\sin(30)}$
$latex \frac{8}{\sin(A)}=\frac{7}{0.5}$
$latex \frac{8}{\sin(A)}=14$
$latex \sin(A)=\frac{8}{14}$
Ahora, usamos la función seno inversa para encontrar el valor del ángulo
$latex A={{\sin}^{-1}}(\frac{8}{14})$
$latex A=34.8$°
El ángulo A mide 34.8°.
EJERCICIO 4
Tenemos los ángulos A=47° y B=78° y tenemos la longitud c=6.3. ¿Cuál es la longitud de a?
Solución
Tenemos los siguientes datos:
- A=47°
- B=78°
- c=6.3
Tenemos un lado que no corresponde a ninguno de los ángulos dados, por lo que tenemos que encontrar el tercer ángulo. Sabemos que los ángulos internos de un triángulo suman 180°, por lo que tenemos:
$latex A+B+C=180$
$latex 47+78+C=180$
$latex C=180-47-78$
$latex C=55$
Ahora, podemos usar la ley de los senos con todos los valores que tenemos:
$latex \frac{a}{\sin(A)}=\frac{c}{\sin(C)}$
$latex \frac{a}{\sin(47)}=\frac{6.3}{\sin(55)}$
$latex \frac{a}{0.73}=\frac{6.3}{0.82}$
$latex \frac{a}{0.73}=7.68$
$latex a=7.68(0.73)$
$latex a=5.6$
El lado a mide 5.6.
Ejercicios de ley de senos para resolver
Usa la fórmula de la ley de senos para resolver los siguientes ejercicios de práctica. Selecciona una respuesta y haz clic en «Verificar» para comprobar que obtuviste la respuesta correcta.
Véase también
¿Interesado en aprender más sobre ley de senos y cosenos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
