La ley de los cosenos es una ecuación que relaciona a las longitudes de dos lados de un triángulo y a su ángulo intermedio. Podemos aplicar la ley de los cosenos cuando queremos encontrar la longitud del tercer lado de un triángulo y conocemos los otros dos lados y su ángulo intermedio. Además, también podemos aplicar la ley de los cosenos cuando queremos encontrar un ángulo y tenemos las longitudes de los tres lados del triángulo.
A continuación, haremos una revisión de la ley de los cosenos. Luego, usaremos su fórmula para resolver algunos ejemplos de práctica.
Resumen de la ley de cosenos
La ley de los cosenos tiene diferentes variaciones dependiendo en los lados y los ángulos que consideremos. Las siguientes son las fórmulas de la ley de cosenos de un triángulo ABC:
| $latex {{a}^2}={{b}^2}+{{c}^2}-2bc\cos(\alpha)$ $latex {{b}^2}={{a}^2}+{{c}^2}-2ac\cos(\beta)$ $latex {{c}^2}={{a}^2}+{{b}^2}-2ab\cos(\gamma)$ |
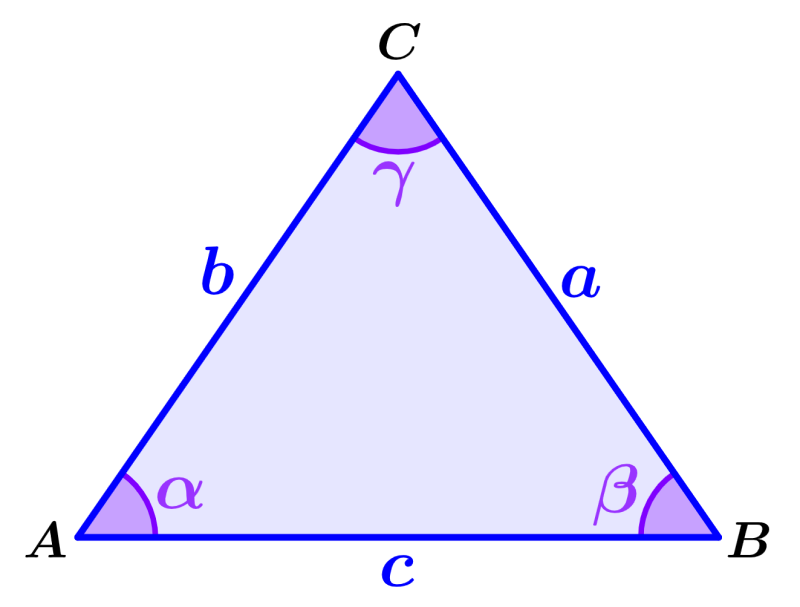
en donde, a, b, c representan a las longitudes de los lados del triángulo y α, β, γ representan a los ángulos del triángulo ABC que se muestra en el siguiente diagrama.
La ley de los cosenos puede ser aplicada cuando tenemos las siguientes situaciones:
- Tenemos las longitudes de dos lados de un triángulo y el ángulo entre estos lados y queremos encontrar la longitud del tercer lado.
- Tenemos las longitudes de los tres lados del triángulo y queremos encontrar la medida de cualquier ángulo.
Por ejemplo, en el triángulo de arriba, podemos aplicar la ley de los cosenos si es que tenemos las longitudes de los lados a y b y la medida del ángulo γ y queremos encontrar la longitud de c.
También, podemos aplicar la ley de los cosenos si es que tenemos las longitudes de a, b, c y queremos encontrar la medida de cualquier ángulo.
Ejemplos de ley de cosenos resueltos
Las fórmulas de la ley de cosenos son usadas para resolver los siguientes ejemplos de aplicación. Cada ejemplo tiene su respectiva respuesta, pero intenta resolver los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
En un triángulo tenemos las longitudes a=8 y b=9 y el ángulo C=50°. ¿Cuál es la longitud de c?
Solución
Tenemos los siguientes valores:
- a=8
- b=9
- C=50°
Encontramos la longitud del lado c usando la ley de cosenos:
$latex {{c}^2}={{a}^2}+{{b}^2}-2ab~\cos(C)$
$latex {{c}^2}={{8}^2}+{{9}^2}-2(8)(9)~\cos(50)$
$latex {{c}^2}=64+81-92.56$
$latex {{c}^2}=52.44$
$latex c=7.24$
La longitud de c es 7.24.
EJERCICIO 2
En un triángulo, tenemos las longitudes b=12 y c=10 y el ángulo A=35°. ¿Cuál es la longitud del lado a?
Solución
Tenemos la siguiente información:
- b=12
- c=10
- A=35°
Usando la ley de cosenos con estos valores, tenemos:
$latex {{a}^2}={{b}^2}+{{c}^2}-2bc~\cos(A)$
$latex {{a}^2}={{12}^2}+{{10}^2}-2(12)(10)~\cos(35)$
$latex {{a}^2}=144+100-196.6$
$latex {{a}^2}=47.4$
$latex a=6.88$
La longitud de a es 6.88.
EJERCICIO 3
¿Cuál es la medida del ángulo A en un triángulo que tiene lados de longitud a=7, b=8 y c=6?
Solución
Tenemos las siguientes longitudes:
- a=7
- b=8
- c=6
Este es un ejemplo en el que tenemos que usar la ley de cosenos para encontrar un ángulo. Entonces, tenemos:
$latex {{a}^2}={{b}^2}+{{c}^2}-2bc~\cos(A)$
$latex {{7}^2}={{8}^2}+{{6}^2}-2(8)(6)~\cos(A)$
$latex 49=64+36-2(8)(6)~\cos(A)$
$latex 49=100-96~\cos(A)$
$latex 96~\cos(A)=51$
$latex A={{\cos}^{-1}}(\frac{51}{96})$
$latex A=57.9$°
El ángulo A mide 57.9°.
EJERCICIO 4
Si es que tenemos los lados a=9, b=11 y c=10 en un triángulo, ¿cuál es la medida del ángulo C?
Solución
Tenemos los siguientes datos:
- a=9
- b=11
- c=10
Usamos a estos valores en la ley de cosenos y resolvemos para el ángulo C:
$latex {{c}^2}={{a}^2}+{{b}^2}-2ab~\cos(C)$
$latex {{10}^2}={{9}^2}+{{11}^2}-2(9)(11)~\cos(C)$
$latex 100=81+121-2(9)(11)~\cos(C)$
$latex 100=202-198~\cos(C)$
$latex 198~\cos(C)=102$
$latex C={{\cos}^{-1}}(\frac{102}{198})$
$latex C=59$°
El ángulo C mide 59°.
Ejemplos de ley de cosenos para resolver
Aplica las diferentes fórmulas de la ley de los cosenos para resolver los siguientes ejemplos. Selecciona una respuesta y verifícala para comprobar que obtuviste la respuesta correcta.
Véase también
¿Interesado en aprender más sobre ley de senos y cosenos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
