La ley de los senos es una ecuación que nos permite relacionar los senos de un ángulo con sus lados opuestos respectivos. La ley de los senos es aplicada para encontrar las medidas de un ángulo o la longitud de un lado en un triángulo. Para usar la ley de los senos, necesitamos conocer las medidas de dos ángulos y la longitud de un lado opuesto o las longitudes de dos lados y la medida de un ángulo opuesto.
A continuación, haremos una revisión de la ley de los senos y la usaremos para resolver algunos ejemplos de práctica.
Resumen de la ley de senos
La ley de los senos es expresada de la siguiente forma:
| $latex \frac{a}{\sin(A)}=\frac{b}{\sin(B)}=\frac{c}{\sin(C)}$ |
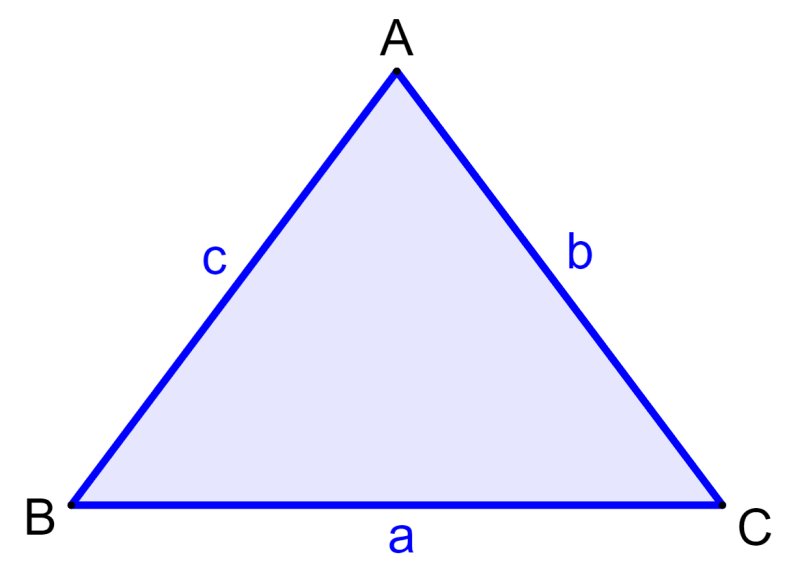
en donde, a, b, c representan las longitudes de los lados del triángulo y A, B, C representan a los ángulos del triángulo. Los lados son denotados usando letras minúsculas con respecto a su ángulo opuesto.
Por ejemplo, a representa al lado opuesto al ángulo A, b representa al lado opuesto al ángulo B y c representa al lado opuesto al ángulo C.
Podemos aplicar la ley de senos cuando tenemos las siguientes situaciones:
- Tenemos la medida de dos ángulos y la longitud de un lado y queremos calcular la longitud de otro lado del triángulo.
- Tenemos la medida de dos lados y un ángulo opuesto a uno de los lados y queremos calcular la medida del otro ángulo.
Por ejemplo, en el triángulo de arriba, podemos usar la ley de los senos si es que tenemos la medida de los ángulos A y B y la longitud del lado a y queremos encontrar la longitud del lado b.
Alternativamente, podemos usar la ley de senos cuando tenemos las longitudes de los lados a, b y la medida del ángulo B y queremos encontrar la medida del ángulo A.
Ejemplos de ley de senos resueltos
Los siguientes ejemplos son resueltos aplicando la ley de los senos. Estos ejemplos pueden ser usados para estudiar el proceso usado para resolver este tipo de problemas. Intenta resolver los ejercicios tú mismo antes de mirar la respuesta.
EJEMPLO 1
En un triángulo, tenemos los ángulos A=50° y B=30° y tenemos al lado a=10. Determina la longitud del lado b.
Solución
Podemos observar la siguiente información:
- A=50°
- B=30°
- a=10
Aplicamos la ley de los senos junto con los valores dados y resolvemos para b:
$latex \frac{a}{\sin(A)}=\frac{b}{\sin(B)}$
$latex \frac{10}{\sin(50)}=\frac{b}{\sin(30)}$
$latex \frac{10}{0.766}=\frac{b}{0.5}$
$latex 13.05=\frac{b}{0.5}$
$latex b=13.05(0.5)$
$latex b=6.53$
La longitud de b es 6.53.
EJEMPLO 2
¿Cuál es la longitud de c si es que tenemos los ángulos B=25° y C=75° y la longitud de b es 12?
Solución
Observamos lo siguiente:
- B=25°
- C=75°
- b=12
Reemplazamos a estos valores en la fórmula de la ley de senos:
$latex \frac{b}{\sin(B)}=\frac{c}{\sin(C)}$
$latex \frac{12}{\sin(25)}=\frac{c}{\sin(75)}$
$latex \frac{12}{0.423}=\frac{c}{0.966}$
$latex 28.37=\frac{c}{0.966}$
$latex c=28.37(0.966)$
$latex c=27.4$
La longitud de c es 27.4.
EJEMPLO 3
¿Cuál es la medida del ángulo A si es que tenemos a=12, B=40° y b=8?
Solución
Tenemos lo siguiente:
- a=12
- B=40°
- b=8
Reemplazamos a estos valores en la fórmula de la ley de senos:
$latex \frac{a}{\sin(A)}=\frac{b}{\sin(B)}$
$latex \frac{12}{\sin(A)}=\frac{8}{\sin(40)}$
$latex \frac{12}{\sin(A)}=\frac{8}{0.643}$
$latex \frac{12}{\sin(A)}=12.44$
$latex \sin(A)=\frac{12}{12.44}$
Usando la función seno inversa, podemos encontrar el valor del ángulo:
$latex A={{\sin}^{-1}}(\frac{12}{12.44})$
$latex A=74.7$°
El ángulo A mide 74.7°.
EJEMPLO 4
Si es que tenemos los ángulos A=36° y B=68° en un triángulo y tenemos la longitud c=11. ¿Cuál es la longitud de a?
Solución
Observamos la siguiente información:
- A=36°
- B=68°
- c=11
Tenemos un lado que no es opuesto a ninguno de los ángulos dados, por lo que vamos a encontrar la medida del tercer ángulo. Para esto, usamos el hecho que los ángulos internos de un triángulo suman 180°. Entonces, tenemos:
$latex A+B+C=180$
$latex 36+68+C=180$
$latex C=180-36-68$
$latex C=76$
Ahora, aplicamos la ley de los senos con los valores que tenemos:
$latex \frac{a}{\sin(A)}=\frac{c}{\sin(C)}$
$latex \frac{a}{\sin(36)}=\frac{11}{\sin(76)}$
$latex \frac{a}{0.588}=\frac{11}{0.97}$
$latex \frac{a}{0.588}=11.34$
$latex a=11.34(0.588)$
$latex a=6.67$
El lado a mide 6.67.
Ejemplos de ley de senos para resolver
Aplica lo aprendido sobre la ley de senos para resolver los siguientes ejercicios de práctica. Selecciona una respuesta y haz clic en «Verificar» para comprobar que obtuviste la respuesta correcta.
Véase también
¿Interesado en aprender más sobre ley de senos y cosenos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
