La ley de los cosenos es la relación entre las longitudes de los lados de un triángulo con respecto al coseno de su ángulo. La ley de cosenos nos dice que el cuadrado de un lado es igual a la suma de los cuadrados de los otros lados menos el doble del producto de estos lados y el coseno del ángulo intermedio. Esta ley es usada cuando queremos encontrar la longitud de un tercer lado y conocemos las longitudes de los dos lados y el ángulo entre ellos.
A continuación, conoceremos la fórmula de la ley de cosenos. Aprenderemos a derivar esta fórmula y la aplicaremos para resolver algunos ejercicios de práctica.
Fórmula de la ley de cosenos
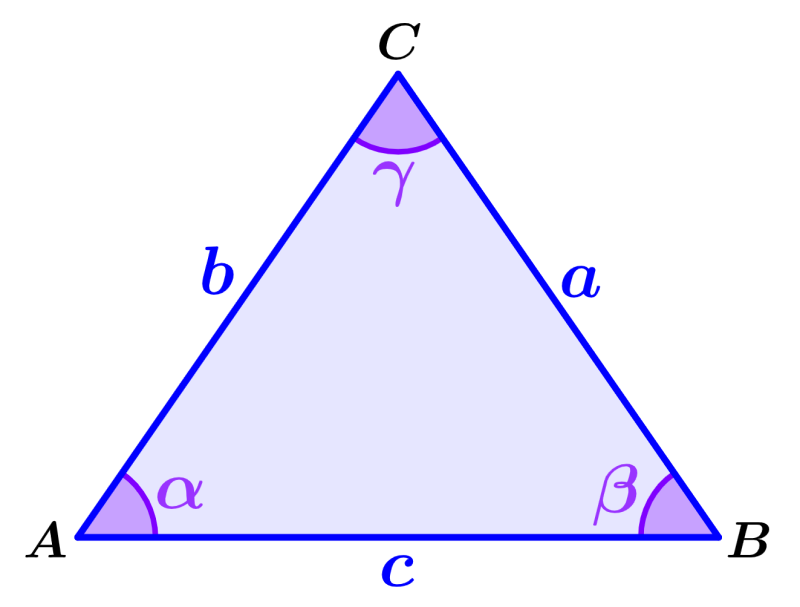
La ley de los cosenos relaciona a las longitudes de dos lados con su ángulo intermedio para encontrar la longitud de un tercer lado. Las fórmulas de la ley de cosenos de un triángulo ABC están dadas por:
| $latex {{a}^2}={{b}^2}+{{c}^2}-2bc\cos(\alpha)$ $latex {{b}^2}={{a}^2}+{{c}^2}-2ac\cos(\beta)$ $latex {{c}^2}={{a}^2}+{{b}^2}-2ab\cos(\gamma)$ |
Aquí, a, b, c son las longitudes de los lados del triángulo y α, β, γ son los ángulos del triángulo ABC que se muestra en el siguiente diagrama.
¿Cuándo se aplica la ley de los cosenos?
Al usar las funciones trigonométricas básicas como el seno, el coseno y la tangente, podemos encontrar información adicional sobre triángulos. La ley de los cosenos se aplica en las siguientes situaciones:
- Cuando tenemos las longitudes de dos lados y su ángulo intermedio y queremos encontrar la longitud del tercer lado.
- Cuando tenemos las longitudes de los tres lados del triángulo y queremos encontrar la medida de cualquier ángulo.
Entonces, un ejemplo de la aplicación de la ley de los cosenos es encontrar la longitud del lado c en el siguiente triángulo si es que conocemos las longitudes de a y b y la medida del ángulo γ.
¿Cómo demostrar la ley de los cosenos?
Para demostrar la ley de los cosenos, vamos a usar el siguiente triángulo:
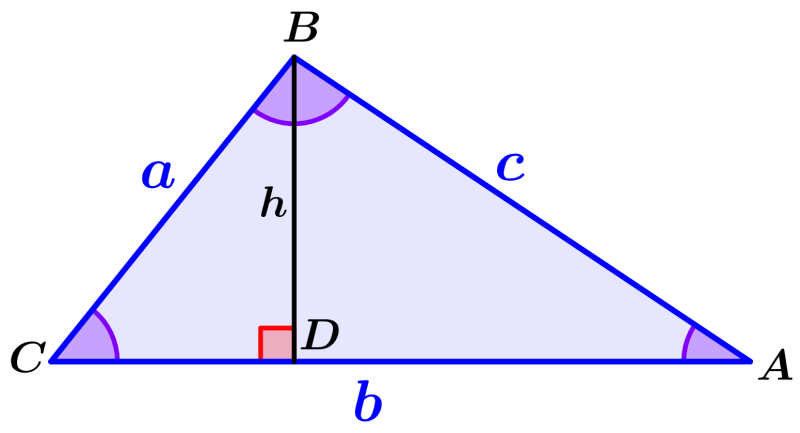
Podemos usar la función coseno en el triángulo BCD. Recordemos que el coseno de un ángulo es igual al lado adyacente dividido por la hipotenusa. Entonces, tenemos:
$latex \cos(C)=\frac{CD}{a}$
$latex CD=a~\cos(C)$
Podemos encontrar la longitud de DA al sustraer a CD de b:
$latex DA=b-CD$
$latex DA=b-a~\cos(C)$
Ahora, usamos a la función seno en el triángulo BCD. Recordemos que el seno de un ángulo es igual al lado opuesto dividido por la hipotenusa. Entonces, tenemos:
$latex \sin(C)=\frac{BD}{a}$
$latex BD=a~\sin(C)$
Aplicamos el teorema de Pitágoras en el triángulo ADB:
$latex {{c}^2}={{BD}^2}+{{DA}^2}$
Usamos las expresiones para BD y DA que obtuvimos anteriormente y las sustituimos en esta ecuación:
$latex {{c}^2}={{(a~\sin(C))}^2}+{{(b-a~\cos(C))}^2}$
Expandiendo en el lado derecho, tenemos:
$$ {{c}^2}={{a}^2}{{\sin}^2}(C)+{{b}^2}-2ab\cos(C)+{{a}^2}{{\cos}^2}(C)$$
Reorganizando a esta ecuación y extrayendo el factor común $latex {{a}^2}$, tenemos:
$${{c}^2}={{a}^2}{{\sin}^2}(C)+{{a}^2}{{\cos}^2}(C)+{{b}^2}-2ab\cos(C)$$
$${{c}^2}={{a}^2}({{\sin}^2}(C)+{{\cos}^2}(C))+{{b}^2}-2ab\cos(C)$$
Podemos simplificar a esta ecuación usando la identidad $latex {{\sin}^2}(\theta)+{{\cos}^2}(\theta)=1$. Entonces, tenemos:
$latex {{c}^2}={{a}^2}+{{b}^2}-2ab\cos(C)$
Con esto, hemos demostrado la ley de cosenos.
Ejercicios de ley de cosenos resueltos
Los siguientes ejercicios son resueltos aplicando las fórmulas de la ley de cosenos. Cada ejercicio tiene su respectiva solución, pero es recomendable que intentes resolver los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
¿Cuál es la longitud del lado c si es que tenemos las longitudes a=6 y b=7 y el ángulo C=40°?
Solución
Empezamos identificando la siguiente información:
- a=6
- b=7
- C=40°
Usando la ley de cosenos, tenemos:
$latex {{c}^2}={{a}^2}+{{b}^2}-2ab~\cos(C)$
$latex {{c}^2}={{6}^2}+{{7}^2}-2(6)(7)~\cos(40)$
$latex {{c}^2}=36+49-64.35$
$latex {{c}^2}=20.65$
$latex c=4.54$
La longitud de c es 4.54.
EJERCICIO 2
Si es que tenemos las longitudes b=10 y c=8 y el ángulo A=25°, ¿cuál es la longitud del lado a?
Solución
Podemos identificar lo siguiente:
- b=10
- c=8
- A=25°
Usando la ley de cosenos, tenemos:
$latex {{a}^2}={{b}^2}+{{c}^2}-2bc~\cos(A)$
$latex {{a}^2}={{10}^2}+{{8}^2}-2(10)(8)~\cos(25)$
$latex {{a}^2}=100+64-145$
$latex {{a}^2}=19$
$latex a=4.36$
La longitud de a es 4.36.
EJERCICIO 3
Tenemos un triángulo con lados de longitud a=5, b=7 y c=6. ¿Cuál es la medida del ángulo A?
Solución
Tenemos lo siguiente:
- a=5
- b=7
- c=6
En este caso, tenemos que usar la ley de cosenos para encontrar un ángulo. Entonces, tenemos:
$latex {{a}^2}={{b}^2}+{{c}^2}-2bc~\cos(A)$
$latex {{5}^2}={{7}^2}+{{6}^2}-2(7)(6)~\cos(A)$
$latex 25=49+36-2(7)(6)~\cos(A)$
$latex 25=85-84~\cos(A)$
$latex 84~\cos(A)=60$
$latex A={{\cos}^{-1}}(\frac{60}{84})$
$latex A=44.4$°
El ángulo A mide 44.4°.
EJERCICIO 4
En un triángulo, tenemos los lados a=10, b=12 y c=8. ¿Cuál es la medida del ángulo C?
Solución
Podemos extraer la siguiente información:
- a=10
- b=12
- c=8
Usamos la ley de cosenos y resolvemos para el ángulo C:
$latex {{c}^2}={{a}^2}+{{b}^2}-2ab~\cos(C)$
$latex {{8}^2}={{10}^2}+{{12}^2}-2(10)(12)~\cos(C)$
$latex 64=100+144-2(10)(12)~\cos(C)$
$latex 64=244-240~\cos(C)$
$latex 240~\cos(C)=180$
$latex C={{\cos}^{-1}}(\frac{180}{240})$
$latex C=41.4$°
El ángulo C mide 41.4°.
Ejercicios de ley de cosenos para resolver
Usa la fórmula de la ley de cosenos para resolver los siguientes ejercicios de práctica. Selecciona una respuesta y haz clic en «Verificar» para comprobar que obtuviste la respuesta correcta.
Véase también
¿Interesado en aprender más sobre ley de senos y cosenos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
