La excentricidad es una característica que determina la forma que tendrán las secciones cónicas. La excentricidad de las hipérbolas depende de la longitud del eje transversal y la longitud del eje conjugado. Por su parte, la longitud de estos ejes puede ser encontrada directamente en la ecuación de una hipérbola o usando las coordenadas de los vértices y los focos.
A continuación, aprenderemos sobre la ecuación que podemos usar para encontrar el valor de la excentricidad de hipérbolas. Luego, veremos algunos ejercicios de práctica.
PRACÁLCULO
Relevante para…
Aprender sobre la excentricidad de la hipérbola con ejercicios.
PRACÁLCULO
Relevante para…
Aprender sobre la excentricidad de la hipérbola con ejercicios.
¿Cómo calcular la excentricidad de las hipérbolas?
La excentricidad de una hipérbola es calculada usando la longitud del eje transversal y la longitud del eje conjugado. Recordemos que las hipérbolas son definidas como el conjunto de puntos en un plano, los cuales tienen una diferencia de las distancias desde los dos focos que es constante.
Esto resulta en que la excentricidad de las hipérbolas siempre sea mayor que 1, es decir, tenemos $latex e>1$.
La ecuación general de una hipérbola es:
$latex \frac{{{x}^2}}{{{a}^2}}-\frac{{{y}^2}}{{{b}^2}}=1$
La fórmula de la excentricidad es:
$latex e=\sqrt{1+\frac{{{b}^2}}{{{a}^2}}}$
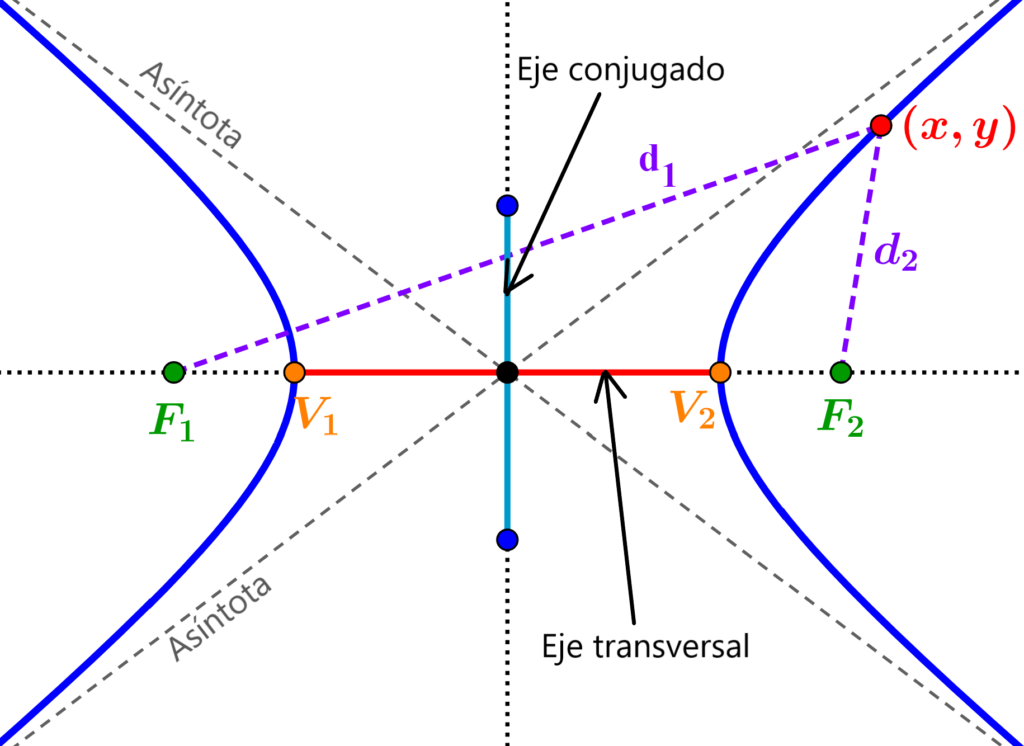
en donde, a es la longitud del eje conjugado y b es la longitud del eje transversal. El eje conjugado es el segmento que conecta a los vértices y el eje transversal es el segmento que conecta a los covértices.
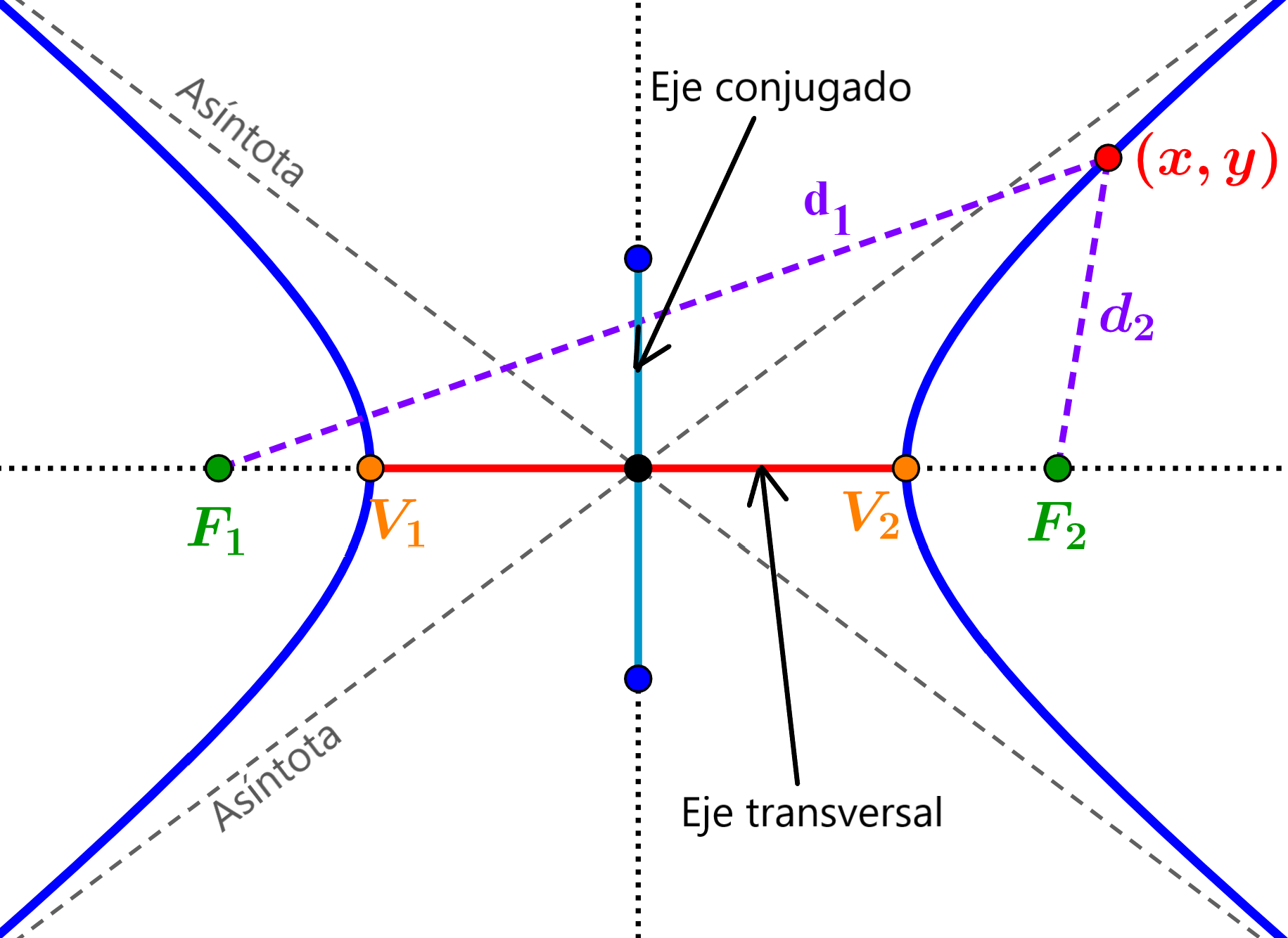
Adicionalmente, también podemos calcular la excentricidad de una hipérbola, usando la siguiente fórmula:
$latex e=\frac{c}{a}$
en donde, c es la longitud del segmento que conecta a los focos y puede ser calculado usando la ecuación $latex {{c}^2}={{a}^2}+{{b}^2}$.
Ejercicios de excentricidad de hipérbolas resueltos
Los siguientes ejercicios son resueltos usando la fórmula de la excentricidad de las hipérbolas. Cada ejercicio tiene su respectiva respuesta, pero es recomendable que intentes resolverlos tú mismo antes de mirar la solución.
EJERCICIO 1
Si es que una hipérbola tiene la ecuación $latex \frac{{{x}^2}}{25}-\frac{{{y}^2}}{16}=1$, ¿cuál es su excentricidad?
Solución
Vemos que la ecuación tiene la forma $latex \frac{{{x}^2}}{{{a}^2}}-\frac{{{y}^2}}{{{b}^2}}=1$, entonces, podemos obtener los siguientes valores:
$latex {{a}^2}=25$
$latex {{b}^2}=16$
Ahora, usamos estos valores en la fórmula de la excentricidad:
$latex e=\sqrt{1+\frac{{{b}^2}}{{{a}^2}}}$
$latex e=\sqrt{1+\frac{16}{25}}$
$latex e=1.28$
EJERCICIO 2
Tenemos a la hipérbola $latex \frac{{{x}^2}}{64}-\frac{{{y}^2}}{25}=1$. ¿Cuál es su excentricidad?
Solución
Nuevamente, tenemos una ecuación con la misma forma que la anterior, por lo que podemos reconocer a los siguientes valores:
$latex {{a}^2}=64$
$latex {{b}^2}=25$
Usando a estos valores en la fórmula de la excentricidad, tenemos:
$latex e=\sqrt{1+\frac{{{b}^2}}{{{a}^2}}}$
$latex e=\sqrt{1+\frac{25}{64}}$
$latex e=1.18$
EJERCICIO 3
¿Cuál es la excentricidad de la hipérbola $latex \frac{{{x}^2}}{121}-\frac{{{y}^2}}{81}=1$?
Solución
Tenemos que determinar los valores de $latex {{a}^2}$ y $latex {{b}^2}$. Entonces, tenemos:
$latex {{a}^2}=121$
$latex {{b}^2}=81$
Usamos la fórmula de la excentricidad con estos valores:
$latex e=\sqrt{1+\frac{{{b}^2}}{{{a}^2}}}$
$latex e=\sqrt{1+\frac{81}{121}}$
$latex e=1.2$
EJERCICIO 4
Si es que una hipérbola tiene la ecuación $latex \frac{{{x}^2}}{120}-\frac{{{y}^2}}{40}=1$, ¿cuál es su excentricidad?
Solución
Reconocemos los siguientes valores al mirar a la ecuación de la hipérbola:
$latex {{a}^2}=120$
$latex {{b}^2}=40$
Ahora, reemplazamos a estos valores en la fórmula de la excentricidad y resolvemos:
$latex e=\sqrt{1+\frac{{{b}^2}}{{{a}^2}}}$
$latex e=\sqrt{1+\frac{40}{120}}$
$latex e=1.15$
Ejercicios de excentricidad de hipérbolas para resolver
Practica el uso de la fórmula de la excentricidad de hipérbolas al resolver los siguientes ejercicios. Selecciona una respuesta y verifícala para comprobar que obtuviste la respuesta correcta.
Véase también
¿Interesado en aprender más sobre hipérbolas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
