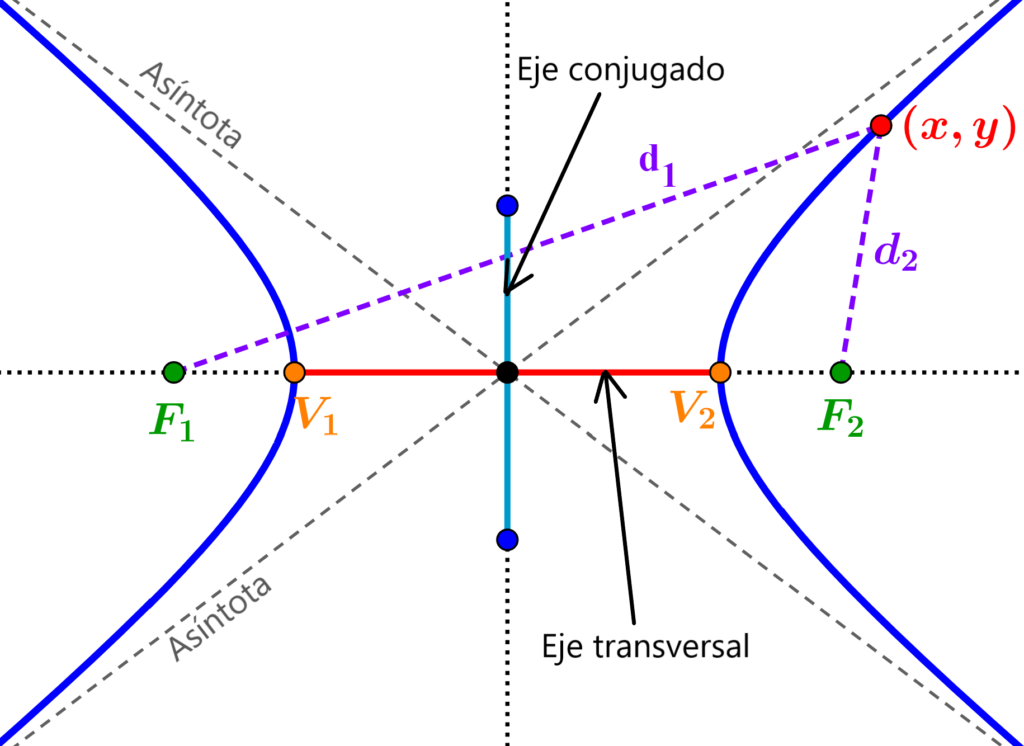
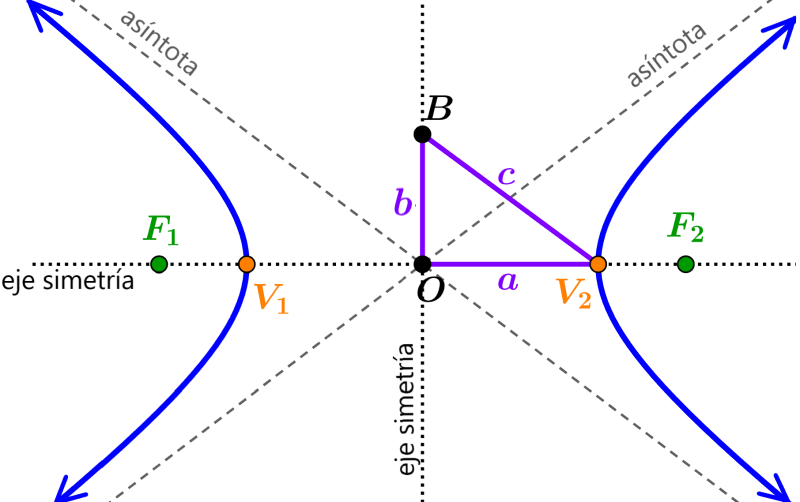
Las asíntotas de las hipérbolas son líneas rectas a las cuales se acerca la curva a medida que los valores de la variable independiente (x) incrementan. Las ramas de la hipérbola se acercan a las asíntotas, pero nunca las tocan. Todas las hipérbolas tienen dos asíntotas, las cuales se intersecan en el centro de la hipérbola. Las ecuaciones de las asíntotas pueden tener cuatro variaciones diferentes dependiendo en la ubicación del centro y en la orientación de la hipérbola.
A continuación, exploraremos las ecuaciones de las hipérbolas junto con algunos ejercicios de práctica.
Asíntotas de hipérbolas centradas en el origen
Las hipérbolas centradas en el origen pueden estar orientadas horizontalmente o verticalmente. Dependiendo de esto, la ecuación de una hipérbola será diferente.
Recordemos que una hipérbola que está centrada en el origen y está orientada horizontalmente tiene la ecuación:
$latex \frac{{{x}^2}}{{{a}^2}}-\frac{{{y}^2}}{{{b}^2}}=1$
en donde, a es la longitud de la distancia desde el centro hasta un vértice y b es la longitud de la distancia desde el centro hasta el covértice. Esta ecuación aplica cuando el eje transversal (segmento que conecta a los vértices) está en el eje x. En este caso, las ecuaciones de las asíntotas son:
$latex y=\pm \frac{b}{a}x$
Cuando la hipérbola está centrada en el origen y está orientada verticalmente, su ecuación es:
$latex \frac{{{y}^2}}{{{a}^2}}-\frac{{{x}^2}}{{{b}^2}}=1$
Esta ecuación aplica cuando el eje transversal está en el eje y. En este caso, las ecuaciones de las asíntotas son:
$latex y=\pm \frac{a}{b}x$
Asíntotas de hipérbolas centradas fuera del origen
Cuando la hipérbola está centrada fuera del origen, podemos aplicar traslaciones para obtener una nueva ecuación. Si es que la hipérbola está orientada horizontalmente, su ecuación es:
$latex \frac{{{(x-h)}^2}}{{{a}^2}}-\frac{{{(y-k)}^2}}{{{b}^2}}=1$
en donde, h es la coordenada en x del centro y k es la coordenada en y del centro. Esta ecuación aplica cuando el eje transversal (segmento que conecta a los vértices) es paralelo al eje x. Las ecuaciones de las asíntotas en este caso son:
$latex y-k=\pm \frac{b}{a}(x-h)$
Por otra parte, si es que la hipérbola está orientada verticalmente, su ecuación es:
$latex \frac{{{(y-k)}^2}}{{{a}^2}}-\frac{{{(x-h)}^2}}{{{b}^2}}=1$
Esta ecuación aplica cuando el eje transversal es paralelo al eje y. Las ecuaciones de las asíntotas en este caso son:
$latex y-k=\pm \frac{a}{b}(x-h)$
Ejercicios de asíntotas de hipérbolas resueltos
Con los siguientes ejercicios, puedes analizar el proceso usado para encontrar las ecuaciones de las asíntotas de hipérbolas. Cada ejercicio tiene su respectiva solución, pero es recomendable que intentes resolver los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
¿Cuál es la ecuación de las asíntotas de la hipérbola $latex \frac{{{x}^2}}{36}-\frac{{{y}^2}}{16}=1$?
Solución
Podemos observar que la ecuación tiene la forma $latex \frac{{{x}^2}}{{{a}^2}}-\frac{{{y}^2}}{{{b}^2}}=1$. Esto significa que la hipérbola está centrada en el origen y está orientada horizontalmente. Entonces, la ecuación de sus asíntotas es:
$latex y=\pm \frac{b}{a}x$
De la ecuación, identificamos los siguientes valores:
$latex {{a}^2}=36$
$latex a=6$
$latex {{b}^2}=16$
$latex b=4$
Reemplazando a estos valores en la ecuación de las asíntotas, tenemos:
$latex y=\pm \frac{4}{6}x$
$latex y=\pm \frac{2}{3}x$
EJERCICIO 2
Si es que una hipérbola tiene la ecuación $latex \frac{{{y}^2}}{25}-\frac{{{x}^2}}{9}=1$, ¿cuáles son sus asíntotas?
Solución
En este caso, la ecuación tiene la forma $latex \frac{{{y}^2}}{{{a}^2}}-\frac{{{x}^2}}{{{b}^2}}=1$. Por lo tanto, la hipérbola está centrada en el origen y está orientada verticalmente. Entonces, la ecuación de sus asíntotas es:
$latex y=\pm \frac{a}{b}x$
De la ecuación, identificamos los siguientes valores:
$latex {{a}^2}=25$
$latex a=5$
$latex {{b}^2}=9$
$latex b=3$
Usando a estos valores en la ecuación de las asíntotas, tenemos:
$latex y=\pm \frac{5}{3}x$
EJERCICIO 3
¿Cuál es la ecuación de las asíntotas de la hipérbola $latex \frac{{{(x-2)}^2}}{64}-\frac{{{(y-3)}^2}}{25}=1$?
Solución
La ecuación de la hipérbola tiene la forma $latex \frac{{{(x-h)}^2}}{{{a}^2}}-\frac{{{(y-k)}^2}}{{{b}^2}}=1$. Esta hipérbola está centrada en (h, k) y está orientada horizontalmente. Entonces, la ecuación de sus asíntotas es:
$latex y-k=\pm \frac{b}{a}(x-h)$
Tenemos los siguientes valores:
$latex {{a}^2}=64$
$latex a=8$
$latex {{b}^2}=25$
$latex b=5$
Al usar estos valores en la ecuación de las asíntotas, tenemos:
$latex y-3=\pm \frac{5}{8}(x-2)$
$latex y=\pm \frac{5}{8}(x-2)+3$
EJERCICIO 4
Si es que una hipérbola tiene la ecuación $latex \frac{{{(y+5)}^2}}{25}-\frac{{{(x-2)}^2}}{9}=1$, ¿cuáles son sus asíntotas?
Solución
En este caso, tenemos la forma $latex \frac{{{(y-k)}^2}}{{{a}^2}}-\frac{{{(x-h)}^2}}{{{b}^2}}=1$. Entonces, tenemos al centro en (h, k) y la hipérbola está orientada verticalmente. Entonces, la ecuación de sus asíntotas es:
$latex y-k=\pm \frac{a}{b}(x-h)$
Tenemos los siguientes valores:
$latex {{a}^2}=25$
$latex a=5$
$latex {{b}^2}=9$
$latex b=3$
Reemplazamos a estos datos en la ecuación de las asíntotas:
$latex y+5=\pm \frac{5}{3}(x-2)$
$latex y=\pm \frac{5}{3}(x-2)-5$
Ejercicios de asíntotas de hipérbolas para resolver
Resuelve los siguientes ejercicios practicando lo aprendido sobre las asíntotas de hipérbolas. Si necesitas ayuda con esto, puedes mirar los ejercicios resueltos de arriba como guía.
Véase también
¿Interesado en aprender más sobre hipérbolas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
