Las hipérbolas son secciones cónicas formadas cuando un plano interseca a un par de conos. Para que la hipérbola sea formada, el plano tiene que intersecar ambas bases de los conos. Las hipérbolas están formadas por dos ramas que tienen la forma de una parábola. Tenemos a un vértice y a un foco en cada rama, los cuales sirven para definir a la hipérbola. También tenemos dos asíntotas, las cuales definen la forma de las ramas. El punto de intersección de las asíntotas es el centro de la hipérbola.
Las hipérbolas aparecen en varios objetos de la vida real. Podemos encontrar figuras hiperbólicas en arquitectura, en varios edificios y estructuras. También encontramos hipérbolas en la explosión sónica de aviones e incluso en la forma de las torres de refrigeración de plantas nucleares.
Estructuras de edificios
Algunos edificios tienen forma de un paraboloide hiperbólico. Un paraboloide hiperbólico es una curva tridimensional que es una hipérbola en una sección transversal y una parábola en otra sección transversal. Un ejemplo de esto es el aeropuerto de Whashington-Dulles en Estados Unidos.
También existen edificios que tienen la forma de un reloj de arena y que contienen ambas ramas de la hipérbola. Un ejemplo de esto es la torre del puerto de Kobe en Japón. La torre es completamente simétrica.
Transmisión de engranajes
Es posible formar una transmisión de engranajes a partir de engranajes hiperbólicos. Los engranajes tienen ejes sesgados y forma de reloj de arena que le dan la forma hiperbólica. Dos hiperboloides pueden transmitir movimiento entre dos ejes inclinados.
Fuente: Wolfram: Computation Meets Knowledge
Explosión sónica
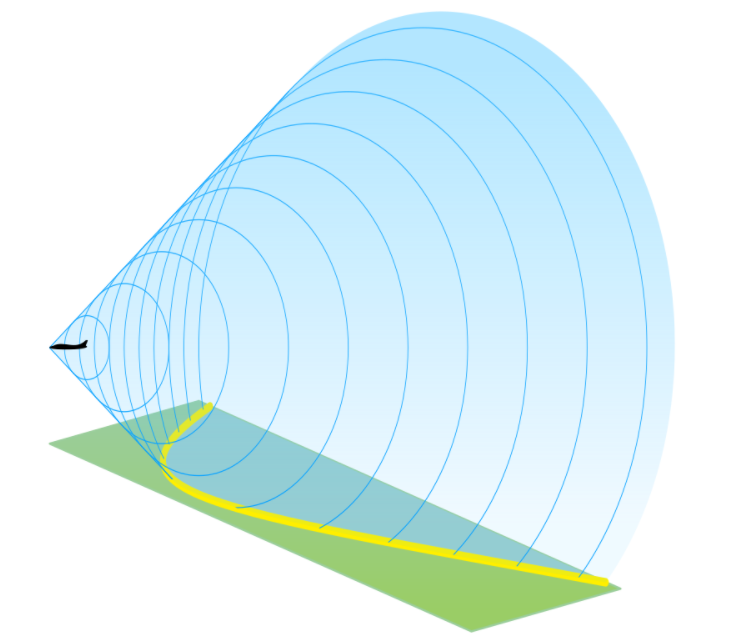
A medida que un avión se mueve más rápido que la velocidad del sonido, una onda en forma de cono es formada. La parte del cono que interseca con el suelo es una hipérbola. La explosión sónica alcanza a cada punto en esa curva al mismo tiempo.
Ningún sonido es escuchado fuera de la curva. La hipérbola es conocida como la «curva de la explosión sónica».
Torres de refrigeración
El hiperboloide es el diseño estándar para todas las torres de refrigeración de plantas nucleares y algunas plantas eléctricas de carbón. Estas torres son estructuralmente eficientes y pueden ser construidas con vigas de acero rectas.
El diseño de las torres de refrigeración se enfoca principalmente en dos problemas:
- La estructura debe ser lo suficientemente fuerte para soportar vientos fuertes.
- Las torres deben ser construidas con la menor cantidad de material posible.
La forma hiperbólica de las torres de refrigeración resuelve ambos problemas. Estas torres son muy resistentes. Para un dado diámetro y altura de la torre y para una fuerza dada que debe soportar, esta forma requiere menos material que cualquier otra forma.
Órbitas de Kepler de partículas
Las órbitas de Kepler son las trayectorias seguidas por cualquier cuerpo orbitante. Esto puede ser aplicado a partículas de cualquier tamaño siempre y cuando la gravedad sea la única fuerza que causa la trayectoria.
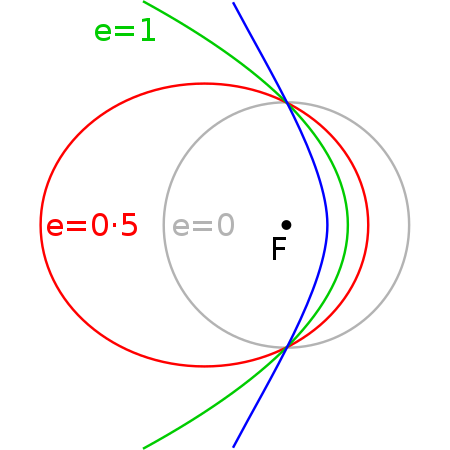
Dependiendo en las propiedades orbitales como el tamaño y la excentricidad, esta órbita puede ser cualquier de las cuatro secciones cónicas. Si es que la excentricidad de la órbita es mayor que 1, la trayectoria del objeto es hiperbólica.
En la siguiente figura, la línea azul es una órbita hiperbólica. El objeto más pesado que causa la trayectoria orbital se ubica en uno de los focos de la hipérbola.
El tipo de órbita de un objeto depende de su nivel de energía. Las órbitas circulares o elípticas son órbitas cerradas, lo que significa que el objeto nunca escapa su trayectoria cerrada alrededor de uno de los puntos focales. Esto se debe a que la energía total del objeto es menor que la energía mínima requerida para escapar y la energía del objeto es considerada negativa en estos casos.
Una trayectoria parabólica tiene la suficiente energía para escapar. Sin embargo, este un caso especial en donde la energía total del objeto es exactamente igual a la energía necesaria para escapar, por lo que la energía es considerada como cero.
Si es que el objeto tiene más energía de la necesaria para escapar, la trayectoria será hiperbólica. Esto significa que la energía total del objeto es positiva.
Otras aplicaciones
- Una guitarra es un ejemplo de una hipérbola ya que sus lados forman las dos ramas de una hipérbola.
- Sistemas satelitales y sistemas de radio usan funciones hiperbólicas.
- Lentes, monitores y lentes ópticos tienen la forma de una hipérbola.
Véase también
¿Interesado en aprender más sobre hipérbolas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
