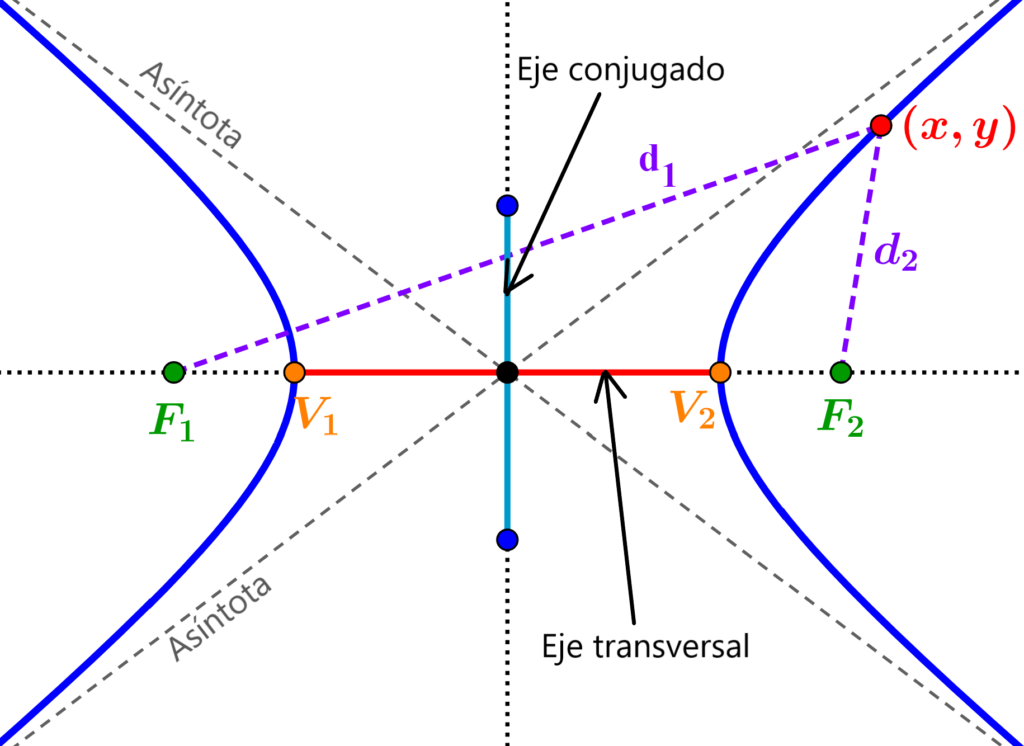
Las hipérbolas consisten de dos piezas que tienen una forma similar a las parábolas. Una pieza se abre hacia arriba y la otra hacia abajo o una hacia la izquierda y la otra hacia la derecha. Además, similar a las parábolas, cada una de las piezas tiene un vértice. Las gráficas de las hipérbolas también tienen dos líneas, las cuales son llamadas asíntotas. Las asíntotas no son parte de las hipérbolas oficialmente, pero son incluidas para asegurarnos de que obtenemos la gráfica correcta. Los elementos más importantes de una hipérbola son los focos, los vértices, los ejes, la longitud focal, los semiejes y las asíntotas.
A continuación, conoceremos más detalles de estos elementos junto con diagramas.
Definición de una hipérbola
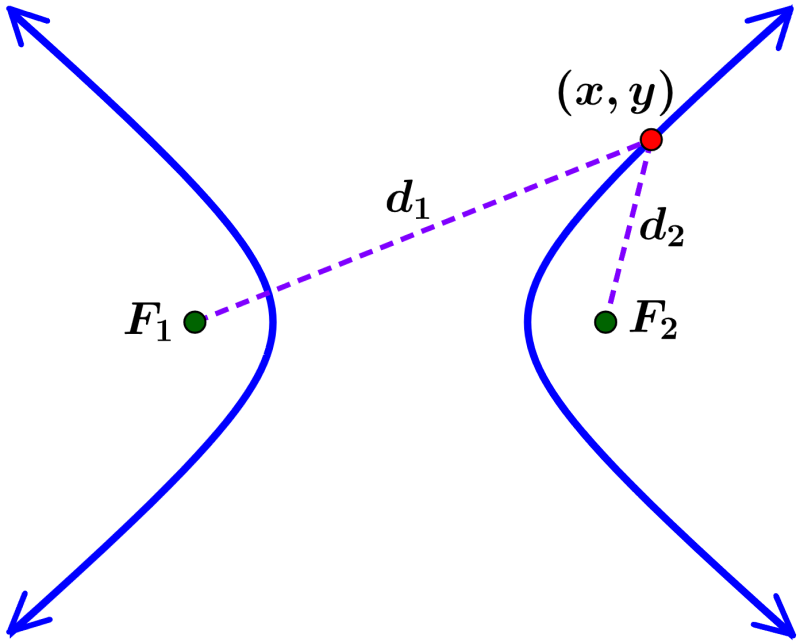
Una hipérbola es el conjunto de todos los puntos, los cuales tienen distancias desde dos puntos fijos, llamados los focos, que tienen una diferencia que es igual a una constante.
Por ejemplo, si es que los puntos $latex F_{1}$ y $latex F_{2}$ son los focos y $latex d$ es una constante, entonces, el punto $latex (x, y)$ es parte de la hipérbola si es que $latex d=|d_{1}-d_{2}|$ como se muestra en la siguiente imagen:
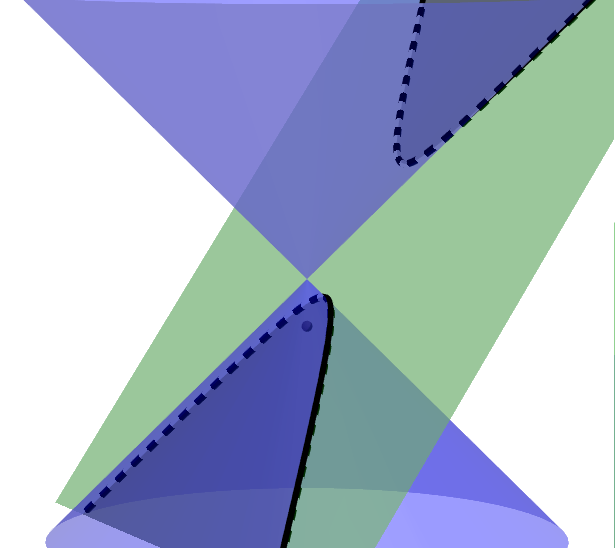
También podemos definir a las hipérbolas como las secciones cónicas que son formadas por la intersección de dos conos con un plano inclinado que interseca a la base de los conos. Las hipérbolas consisten de dos curvas separadas, llamadas ramas.
Los puntos en los cuales la distancia es la mínima entre las dos ramas son llamados los vértices. El punto medio de los vértices de la hipérbola es el centro. Una hipérbola es asintótica con respecto a ciertas líneas trazadas a través del centro.
Elementos fundamentales de una hipérbola
Los siguientes son los elementos fundamentales de una hipérbola:
- Focos
- Eje transversal
- Eje conjugado
- Semieje mayor
- Semieje menor
- Centro
- Vértices
- Longitud focal
- Ejes de simetría
- Asíntotas
Focos
Los focos son los puntos fijos usados para definir a la hipérbola. Los focos son frecuentemente definidos por $latex F_{1}$ y $latex F_{2}$ o también por $latex F$ y $latex F’$.
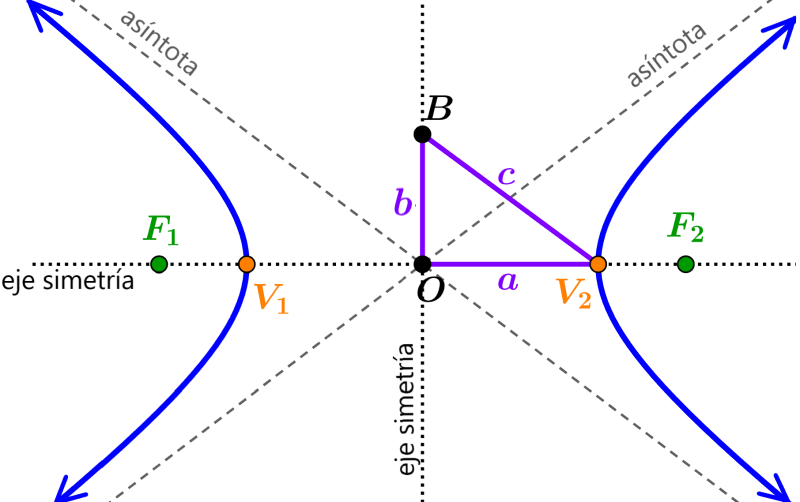
Las coordenadas de los focos están dadas por $latex F=(h\pm c,k)$ si es que el eje transversal es paralelo al eje x y por $latex F=(h, k\pmc)$ si es que el eje transversal es paralelo al eje y. El punto $latex (h, k)$ es el centro y encontramos a c usando $latex {{c}^2}={{a}^2}+{{b}^2}$.
Eje transversal
El eje transversal, también conocido como el eje real, es el segmento que se extiende entre los dos focos. El eje transversal puede ser determinado usando la ecuación de la hipérbola. Sabemos que la ecuación de la hipérbola contiene un término negativo y otro positivo.
Si es que el signo positivo está en el término x, significa que el eje transversal está en el eje x y si es que el signo positivo está en el término y, significa que el eje transversal está en el eje y.
Eje conjugado
El eje conjugado, también conocido como el eje imaginario, es el bisector perpendicular del eje transversal. El eje conjugado divide al eje transversal en dos partes iguales.
Semieje mayor
El semieje mayor es el segmento que se extiende desde el centro hasta un vértice de la hipérbola. Su longitud es denotada con la a.
Semieje menor
El semieje menor es el segmento perpendicular al semieje mayor. Su longitud es denotada con la b.
Centro
El centro tiene dos ejes de simetría. El centro es el punto de intersección de los dos ejes de simetría. Si es que la hipérbola está centrada en el origen, el centro es (0,0) y si es que está centrado en otro punto, el centro es $latex (h,k)$.
Vértices
Los vértices son los puntos de intersección de la hipérbola con el eje transversal. Los vértices son los puntos extremos de cada rama de la hipérbola. Usualmente, usamos $latex V_{1}$ y $latex V_{2}$ o $latex V$ y $latex V’$ para representar a los vértices.
Longitud focal
La longitud focal es la longitud del segmento que se extiende desde un foco ($latex F_{1}$) hasta el otro foco ($latex F_{2}$). Su longitud es igual a 2c.
Ejes de simetría
Los ejes de simetría son los ejes que coinciden con el eje transversal y el eje conjugado. Las dos ramas de la hipérbola son simétricas. Las hipérbolas tienen dos ejes de simetría, el eje horizontal y el eje vertical. El punto de intersección de estos ejes es el centro.
Asíntotas
Las asíntotas son las líneas que están muy cerca a las ramas de la hipérbola, pero que nunca la tocan. Las asíntotas se intersecan en el centro de la hipérbola.
Véase también
¿Interesado en aprender más sobre hipérbolas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
