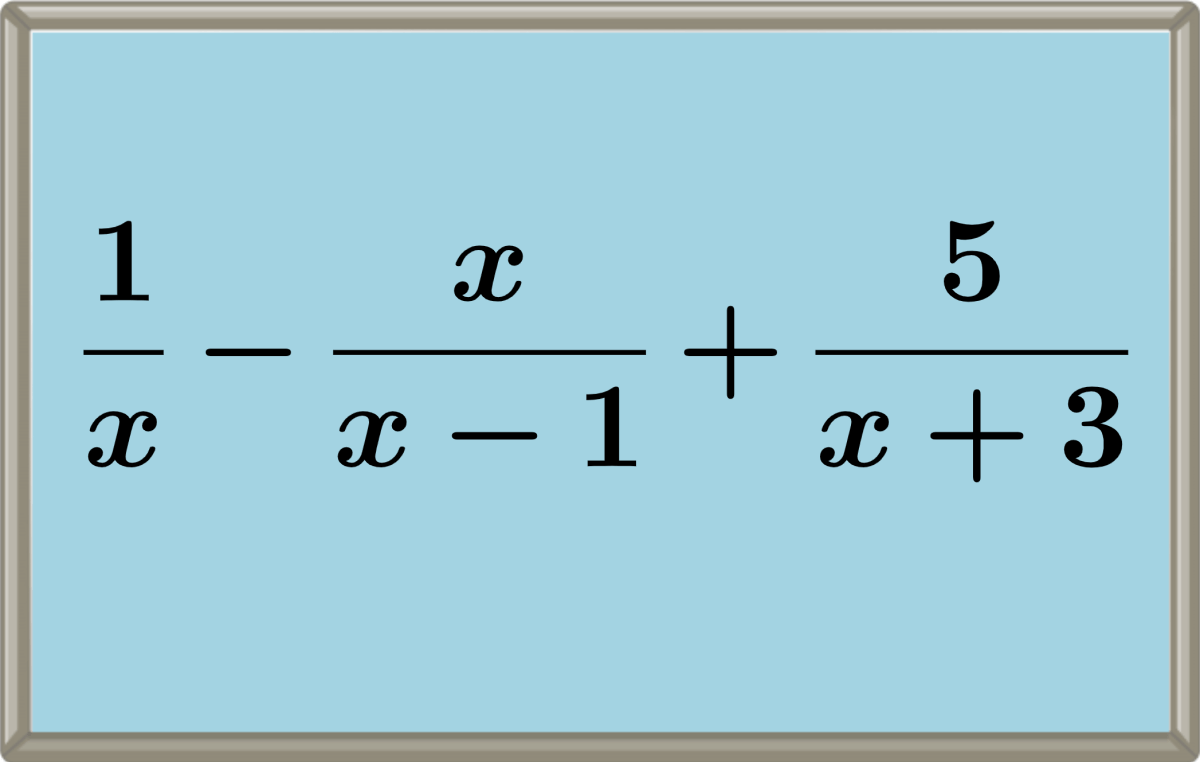Sumas de fracciones algebraicas – Ejercicios resueltos

Cuando las fracciones algebraicas a sumar tienen el mismo denominador, sea este un número o una expresión algebraica, encontrar su suma es muy fácil, ya que bastará con escribir el mismo denominador y sumar los numeradores.

En este caso, el denominador de ambas expresiones algebraicas es el 3, entonces, tenemos:

$$\frac {x-1}{3}+\frac{1-8x}{3}=\frac{(x-1)+(1-8x)}{3}$$

Seguidamente, se reducen los términos semejantes en el numerador, de esta forma:

$$\frac {x-1}{3}+\frac{1-8x}{3}=\frac{(x-1)+(1-8x)}{3}$$

$$=\frac{(x-8x)+(-1+1)}{3}$$

$$=-\frac{7x}{3}$$

Por lo tanto:

$$\frac {x-1}{3}+\frac{1-8x}{3}=-\frac{7x}{3}$$

Los denominadores de ambas fracciones son los mismos, por lo tanto:

$$\frac {4x^2-3}{x}+\frac{2x^2-1}{x} =\frac {(4x^2-3)+(2x^2-1)}{x}$$

Combinando términos semejantes, tenemos:

$$\frac {(4x^2-3)+(2x^2-1)}{x}=\frac {(4x^2+2x^2)+(-3-1)}{x}$$

$$=\frac {6x^2-4}{x}$$

La suma solicitada es:

$$\frac {4x^2-3}{x}+\frac{2x^2-1}{x}=\frac {6x^2-4}{x}$$

Tratándose de sumandos con igual denominador, se procede como en los ejemplos anteriores:

$$\frac {y}{y-6}+\frac{6+4y-y^2}{y-6}=\frac {y+6+4y-y^2}{y-6}$$

Seguidamente, se suman los términos semejantes en el numerador:

$$\frac {y+6+4y-y^2}{y-6}=\frac {6+5y-y^2}{y-6}$$

$$=\frac {-y^2+5y+6}{y-6}$$

Ahora bien, si en el numerador se saca el factor común $latex (-1)$, queda un trinomio que se puede factorizar:

$$=\frac {-y^2+5y+6}{y-6}= \frac {(-1)\cdot (y^2-5y-6)}{y-6} $$

En efecto:

$$y^2-5y-6 = (y-6)\cdot(y+1) $$

Sustituyendo en la suma y simplificando:

$$\frac {(-1)\cdot(y^2-5y-6)}{y-6} =\frac { (-1)\cdot(y-6)(y+1)}{y-6}$$

$$=-y-1$$

Entonces:

$$\frac {y}{y-6}+\frac{6+4y-y^2}{y-6}=-y-1$$

Este es un ejemplo de suma de fracciones algebraica con distinto denominador, por lo que, en primer lugar, se determina el mínimo común múltiplo (mcm) de los denominadores.

Siendo estos 2 y 7, primos entre sí, el mínimo común múltiplo de ambos es el producto de los valores:

$latex mcm(2,7) = 2\times 7 = 14$

Por lo tanto, el denominador de la suma buscada será 14. Para hallar el numerador de la suma, se divide este valor entre el denominador de la primera fracción y se multiplica el resultado por el numerador correspondiente.

Este procedimiento se repite para la siguiente fracción, y los resultados se suman, así:

$$\frac {x+3}{2}+\frac{5x+1}{7}=\frac{7(x+3)+2(5x+1)}{14}$$

Seguidamente, se aplica la propiedad distributiva en el numerador, y se suman los términos semejantes:

$$\frac {x+3}{2}+\frac{5x+1}{7}=\frac{7(x+3)+2(5x+1)}{14}$$

$$=\frac{7x+21+10x+2)}{14}$$

$$=\frac{17x+23}{14}$$

El resultado buscado es:

$$\frac {x+3}{2}+\frac{5x+1}{7}=\frac{17x+23}{14}$$

Se trata de una suma de fracciones algebraicas con diferente denominador, por lo tanto, es necesario hallar el mcm de tres expresiones algebraicas.

No es difícil darse cuenta de que dicha expresión algebraica es $latex 6x^3$, por lo tanto:

$latex mcm[2x; x^2; 6x^3]=6x^3$

Al dividir el mcm obtenido entre cada uno de los denominadores de los sumandos, vemos que la división es exacta:

• $latex 6x^3\div 2x = 3x^2$
• $latex 6x^3\div x^2 = 6x$
• $latex 6x^3\div 6x^3 = 1$

El denominador de la suma será el mcm, mientras que en el numerador es la suma de los productos entre los respectivos numeradores y cada uno de los resultados obtenidos:

$$\frac{3}{2x}+\frac{4}{x^2}+\frac{5}{6x^3}=\frac{3\cdot 3x^2+4\cdot 6x +5\cdot 1}{6x^3}$$

$$=\frac{9x^2+24x +5}{6x^3}$$

El numerador es irreducible, por lo que se concluye que:

$$\frac{3}{2x}+\frac{4}{x^2}+\frac{5}{6x^3}=\frac{9x^2+24x +5}{6x^3}$$

Nótese que $latex y^2-9$ es una diferencia de cuadrados perfectos, y como tal, se puede factorizar de la siguiente manera:

$latex y^2-9 = (y+3)(y-3)$

La suma se puede escribir de esta manera, que es equivalente:

$$\frac {2y}{y-3}+\frac{3y}{y+3}+\frac{10y}{y^2-9}=\frac {2y}{y-3}+\frac{3y}{y+3}+\frac{10y}{(y+3)(y-3)}$$

Los tres denominadores son diferentes, en consecuencia, es necesario encontrar el mínimo común múltiplo entre ellos:

$$mcm[(y-3);(y+3);(y+3)(y-3)]=(y+3)(y-3)$$

El denominador de la fracción resultante es el mcm de los denominadores de las tres fracciones.

En cuanto al numerador, hay que dividir el mcm entre cada uno de los denominadores y multiplicar por el respectivo numerador, luego se suma todo, tal como en el ejercicio anterior:

$$\frac {2y}{y-3}+\frac{3y}{y+3}+\frac{10y}{y^2-9}=\frac {(y+3)2y+(y-3)3y+10y}{(y+3)(y-3)}$$

El siguiente paso es aplicar la propiedad distributiva en el numerador para desarrollarlo:

$$\frac {(y+3)2y+(y-3)3y+10y}{(y+3)(y-3)}=\frac {2y^2+6y+3y^2-9y+10y}{(y+3)(y-3)}$$

$$=\frac {5y^2+7y}{(y+3)(y-3)}$$

La expresión obtenida es irreducible, ya que entre el numerador y el denominador no hay factores comunes, sin embargo, el numerador puede factorizarse para obtener finalmente:

$$\frac {2y}{y-3}+\frac{3y}{y+3}+\frac{10y}{y^2-9}=\frac {y(5y+7)}{(y+3)(y-3)}$$

Puesto que los denominadores son distintos y no tienen factores en común, el mcm es simplemente el producto entre ellos:

$latex mcm[x; (x-3)]=x(x-3)$

Por lo tanto, la suma buscada es:

$$\frac{10}{x}+\frac{2x}{x-3}=\frac{10(x-3)+2x\cdot x}{x(x-3)}$$

$$=\frac{2x^2+10x-30}{x(x-3)}$$

Se puede factorizar el numerador:

$$\frac{2x^2+10x-30}{x(x-3)}=\frac{2(x^2+5x-15)}{x(x-3)}$$

Luego:

$$\frac{10}{x}+\frac{2x}{x-3}=\frac{2(x^2+5x-15)}{x(x-3)}$$

A primera vista, parece que los denominadores de ambas fracciones son distintos, sin embargo, multiplicando al numerador y al denominador de la segunda fracción por $latex (-1)$, los denominadores se igualan y tenemos:

$$\frac{9}{z-2}+\frac{3z}{2-z}=\frac{9}{z-2}+\frac{(-1)\cdot(3z)}{(-1)\cdot(2-z)}$$

$$=\frac{9}{z-2}+\frac{(-3z)}{(z-2)}$$

$$=\frac{9-3z}{z-2}$$

$$=\frac{3(3-z)}{z-2}$$

La operación se puede escribir como:

$$\frac{9}{z-2}+\frac{3z}{2-z}=\frac{3(3-z)}{z-2}$$

El primer sumando no es una fracción, pero se puede escribir como tal colocando un $latex 1$ en el denominador:

$$5y^2+\frac{9y}{y-6}=\frac {5y^2}{1}+\frac{9y}{y-6}$$

Enseguida se calcula el $latex mcm$ de los denominadores:

$latex mcm (1; y-6)= y-6$

Por lo tanto:

$$5y^2+\frac{9y}{y-6}=\frac {5y^2}{1}+\frac{9y}{y-6}$$

$$=\frac {5y^2(y-6)+9y}{y-6}$$

$$=\frac {5y^3-30y^2+9y}{y-6}$$

$$=\frac {y(5y^2-30y+9)}{y-6}$$

En primer lugar, de ser posible se factorizan los denominadores:

$$x^2+2x-8 =(x+4)\cdot(x-2)$$

$$x^2-3x+2 =(x-2)\cdot(x-1)$$

Y se reescribe la expresión:

$$\frac{x}{x^2+2x-8}+\frac{x+1}{x^2-3x+2}=\frac{x}{(x+4)(x-2)}+\frac{x+1}{(x-2)(x-1)}$$

De esta manera, el mínimo común múltiplo de los denominadores es:

$$mcm[(x+4)(x-2);(x-2)(x-1)] =(x-2)(x+4)(x-1)$$

Por lo tanto:

$$\frac{x}{(x+4)(x-2)}+\frac{x+1}{(x-2)(x-1)}=\frac{x(x-1)+(x+1)(x+4)}{(x-2)(x+4)(x-1)}$$

Ahora se desarrollan los productos que aparecen en el numerador:

$latex x(x-1)=x^2-x$

$latex (x+1)(x+4)=x^2+5x+4$

Y se suman, reduciendo los términos semejantes:

$$(x^2-x)+(x^2+5x+4) = 2x^2+4x+4= 2(x^2+2x+2)$$

Se sustituye este resultado en el numerador:

$$\frac{x}{(x+4)(x-2)}+\frac{x+1}{(x-2)(x-1)}=\frac{x(x-1)+(x+1)(x+4)}{(x-2)(x+4)(x-1)}$$

$$=\frac{2(x^2+2x+2)}{(x-2)(x+4)(x-1)}$$

El numerador no se factoriza más, por lo tanto:

$$ \frac{x}{x^2+2x-8}+\frac{x+1}{x^2-3x+2}=\frac{2(x^2+2x+2)}{(x-2)(x+4)(x-1)}$$