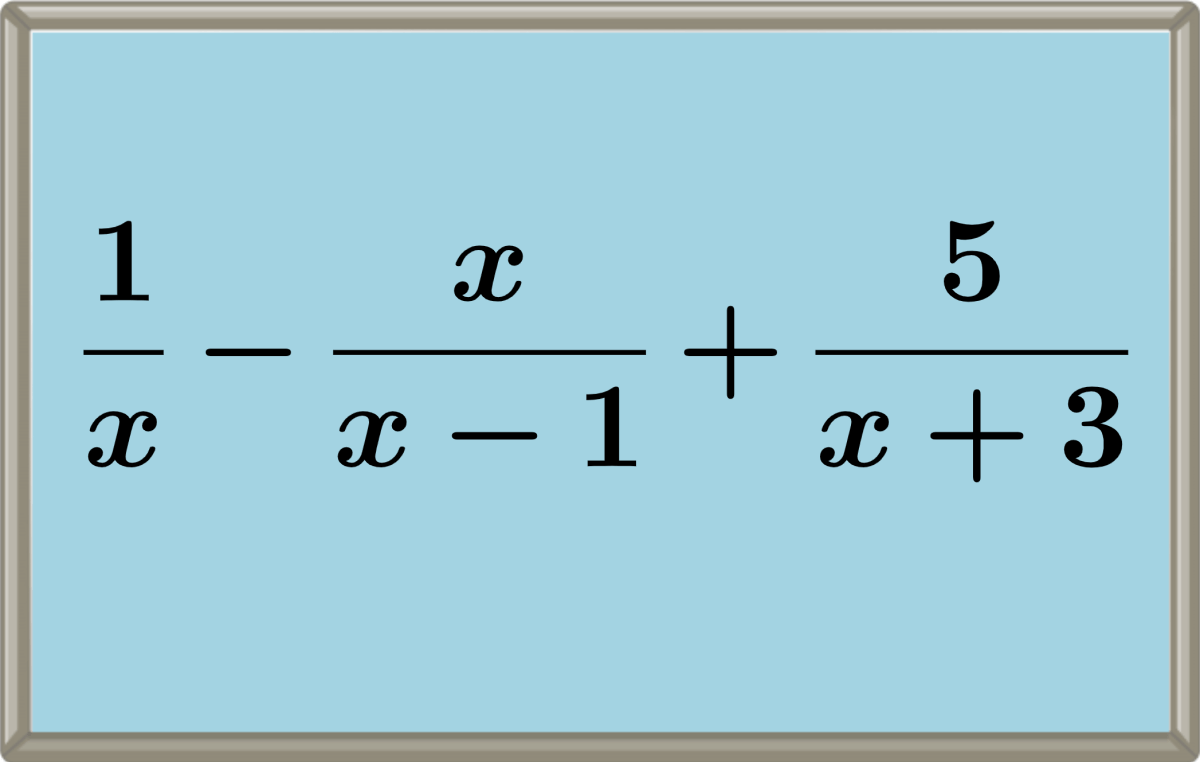El proceso para sumar y restar fracciones algebraicas depende de si las fracciones son homogéneas (con el mismo denominador) o heterogéneas (con denominadores diferentes). Si las fracciones son heterogéneas, tenemos que empezar calculando el mínimo común denominador.
A continuación, conoceremos los pasos que podemos seguir para sumar y restar tanto fracciones homogéneas, como fracciones heterogéneas. Luego, veremos algunos ejemplos prácticos.
Pasos para sumar y restar fracciones algebraicas homogéneas
Fracciones homogéneas son fracciones que tienen los mismos denominadores. Por ejemplo, las fracciones $latex \frac{1}{x+1}$ y $latex \frac{3}{x+1}$ son fracciones homogéneas.
Para sumar y restar este tipo de fracciones, simplemente tenemos que «combinar» las fracciones al usar un solo denominador y realizar las operaciones del numerador.
Entonces, podemos seguir los siguientes pasos para sumar y restar fracciones algebraicas homogéneas:
1. Escribir a las fracciones usando un solo denominador.
Dado que el denominador es el mismo, podemos «combinar» a las fracciones en una sola.
2. Realizar las operaciones del numerador.
Simplificar y combinar términos semejantes.
3. Simplificar el resultado final.
Pasos para sumar y restar fracciones algebraicas heterogéneas
Fracciones heterogéneas son fracciones que tienen diferentes denominadores. Por ejemplo, las fracciones $latex \frac{1}{x+2}$ y $latex \frac{3}{x-3}$ son fracciones heterogéneas.
Para sumar y restar este tipo de fracciones, tenemos que empezar encontrando el mínimo común múltiplo de los denominadores. Luego, reescribimos a las fracciones para obtener fracciones homogéneas.
Entonces, podemos sumar y restar fracciones algebraicas heterogéneas al aplicar los siguientes pasos:
1. Encuentra el mínimo común denominador (mcd).
2. Usa el mínimo común denominador para escribir fracciones homogéneas.
El nuevo denominador de cada fracción es el mcd. El nuevo numerador de cada fracción es igual al mcd dividido por el denominador y multiplicado por el numerador de la fracción original.
3. Escribe a las fracciones usando un solo denominador.
Como el denominador de las fracciones del paso 2 es el mismo, las combinamos para obtener una sola fracción.
4. Realiza las operaciones del numerador.
Simplificar y combinar términos semejantes.
5. Simplificar la fracción final.
Ejercicios resueltos de suma y resta de fracciones algebraicas
EJERCICIO 1
¿Cuál es el resultado de la suma de fracciones? $$\frac{3x+2}{5}+\frac{x}{5}$$
Solución
Tenemos una suma de fracciones homogéneas. Entonces, podemos escribirlas usando un solo denominador de la siguiente forma:
$$\frac{3x+2}{5}+\frac{x}{5}=\frac{3x+2+x}{5}$$
Ahora, combinamos términos semejantes en el numerador:
$$\frac{3x+2+x}{5}=\frac{4x+2}{5}$$
La fracción ya no puede ser simplificada, por lo que $latex \frac{4x+2}{5}$ es nuestro resultado final.
EJERCICIO 2
Encuentra el resultado de la resta de fracciones: $$\frac{4x+1}{x+2}-\frac{3-2x}{x+2}$$
Solución
En este caso, tenemos una resta de fracciones homogéneas, entonces, podemos combinarlas para formar una sola fracción:
$$\frac{4x+1}{x+2}-\frac{3-2x}{x+2}=\frac{4x+1-(3-2x)}{x+2}$$
$$=\frac{4x+1-3+2x}{x+2}$$
Combinando términos semejantes en el numerador, tenemos:
$$\frac{4x+1-3+2x}{x+2}=\frac{6x-2}{x+2}$$
Podemos simplificar el numerador: $latex \frac{2(3x-1)}{x+2}$ y este es nuestro resultado final.
EJERCICIO 3
Realiza la siguiente suma de fracciones: $$\frac{3}{x-1}+\frac{2}{x+3}$$
Solución
En este caso, tenemos una suma de fracciones heterogéneas. Entonces, tenemos que empezar encontrando el mínimo común denominador.
El mínimo común denominador es $latex (x-1)(x+3)$, ya que puede ser dividido por ambos denominadores sin dejar residuo.
Luego, formamos fracciones homogéneas al dividir al mcd por cada denominador y multiplicar por el numerador. Entonces, tenemos:
$$\frac{3}{x-1}+\frac{2}{x+3}=\frac{3(x+3)}{(x-1)(x+3)}+\frac{2(x-1)}{(x-1)(x+3)}$$
Combinando las fracciones homogéneas y realizando las operaciones del numerador, tenemos:
$$=\frac{3(x+3)+2(x-1)}{(x-1)(x+3)}$$
$$=\frac{3x+9+2x-2}{(x-1)(x+3)}$$
$$=\frac{5x+7}{(x-1)(x+3)}$$
Ya no podemos simplificar la fracción. Entonces, $latex \frac{5x+7}{(x-1)(x+3)}$ es nuestro resultado final.
EJERCICIO 4
Realiza la siguiente resta de fracciones: $$\frac{4}{x+6}-\frac{2}{x+7}$$
Solución
Como tenemos una resta de fracciones heterogéneas, empezamos encontrando el mínimo común denominador.
En este caso, el mínimo común denominador es $latex (x+6)(x+7)$. Entonces, formamos fracciones homogéneas usando ese denominador:
$$\frac{4}{x+6}-\frac{2}{x+7}=\frac{4(x+7)}{(x+6)(x+7)}-\frac{2(x+6)}{(x+6)(x+7)}$$
Ahora, podemos formar una sola fracción y simplificar el numerador:
$$=\frac{4(x+7)-2(x+6)}{(x+6)(x+7)}$$
$$=\frac{4x+28-2x-12}{(x+6)(x+7)}$$
$$=\frac{2x+16}{(x+6)(x+7)}$$
$$=\frac{2(x+8)}{(x+6)(x+7)}$$
EJERCICIO 5
Encuentra el resultado de la siguiente suma de fracciones: $$\frac{2x}{x^2+3x+2}+\frac{3}{x+1}$$
Solución
Para encontrar el mínimo común denominador, podemos empezar reconociendo que:
$$x^2+3x+2=(x+1)(x+2)$$
Esto significa que $latex (x+1)$ es un factor de $latex x^2+3x+2$ y $latex (x+1)(x+2)$ es el mínimo común denominador. Entonces, tenemos:
$$\frac{2x}{x^2+3x+2}+\frac{3}{x+1}=\frac{2x}{(x+1)(x+2)}+\frac{3(x+2)}{(x+1)(x+2)}$$
Combinando las fracciones homogéneas y realizando las operaciones del numerador, tenemos:
$$=\frac{2x+3(x+2)}{(x+1)(x+2)}$$
$$=\frac{2x+3x+6}{(x+1)(x+2)}$$
$$=\frac{5x+6}{(x+1)(x+2)}$$
EJERCICIO 6
Encuentra el resultado de la siguiente suma y resta de fracciones: $$x+7+\frac{1}{x-4}-\frac{5}{x+1}$$
Solución
Podemos escribir a esta expresión de la siguiente forma:
$$\frac{x+7}{1}+\frac{1}{x-4}-\frac{5}{x+1}$$
Entonces, el mínimo común denominador es $latex (x-4)(x+1)$ y tenemos lo siguiente:
Luego, formamos fracciones homogéneas al dividir al mcd por cada denominador y multiplicar por el numerador. Entonces, tenemos:
$$\frac{x+7}{1}+\frac{1}{x-4}-\frac{5}{x+1}$$
$$=\frac{(x+7)(x-4)(x+1)+(x+1)-5(x-4)}{(x-4)(x+1)}$$
$$=\frac{x^3+4x^2-25x-28+x+1-5x+20}{(x-4)(x+1)}$$
$$=\frac{x^3+4x^2-29x-7}{(x-4)(x+1)}$$
Puedes explorar ejercicios adicionales de este tema en estos artículos: Ejercicios de sumas de fracciones algebraicas, Ejercicios de restas de fracciones algebraicas.
Suma y resta de fracciones algebraicas – Ejercicios para resolver
¿Cuál es el numerador de la fracción obtenida al realizar la siguiente operación? $$\frac{5x}{2x^2+3x-5}-\frac{1}{x-1}-\frac{2}{2x+5}$$
Escribe el numerador en la casilla.
Véase también
¿Interesado en aprender más sobre fracciones algebraicas? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
