Para multiplicar dos o más fracciones algebraicas, simplemente multiplicamos los numeradores y los denominadores separadamente. Luego, simplificamos la fracción resultante al eliminar factores comunes en el numerador y denominador.
A continuación, veremos algunos ejercicios de multiplicación de fracciones algebraicas. Además, exploraremos ejercicios de práctica para aplicar lo aprendido.
ÁLGEBRA
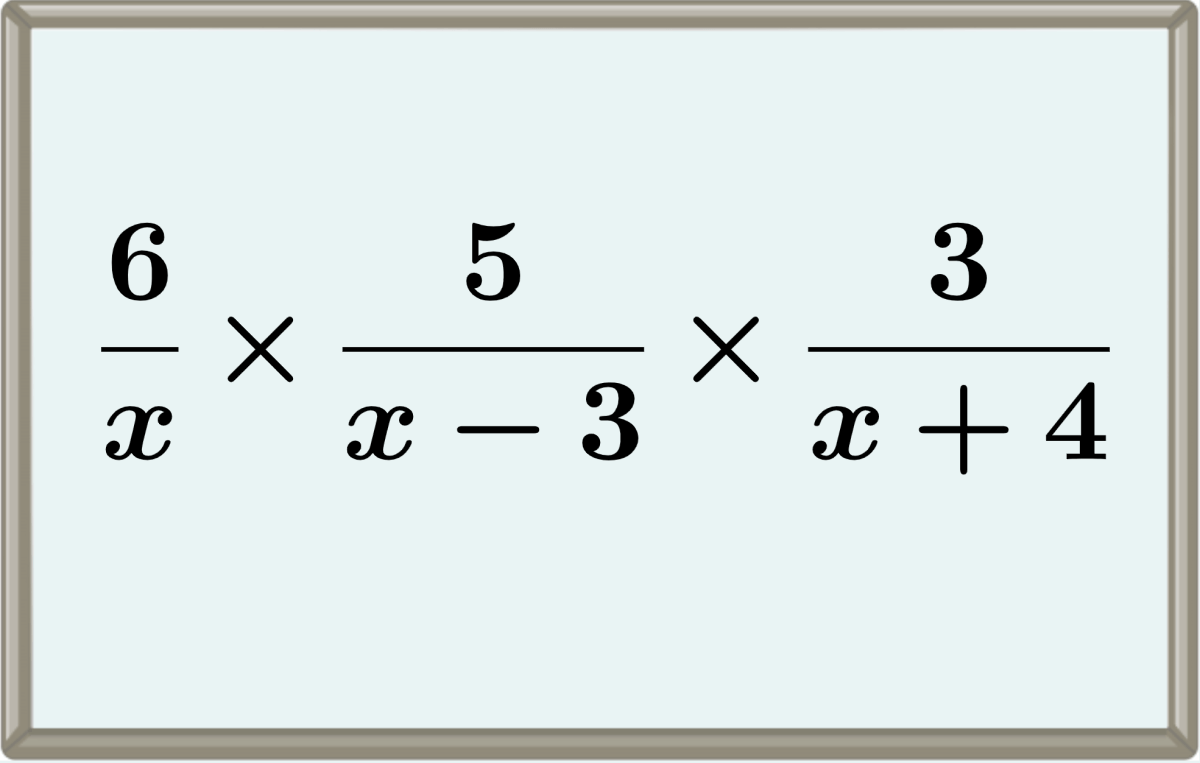
Relevante para…
Resolver ejercicios de multiplicación de fracciones algebraicas.
ÁLGEBRA
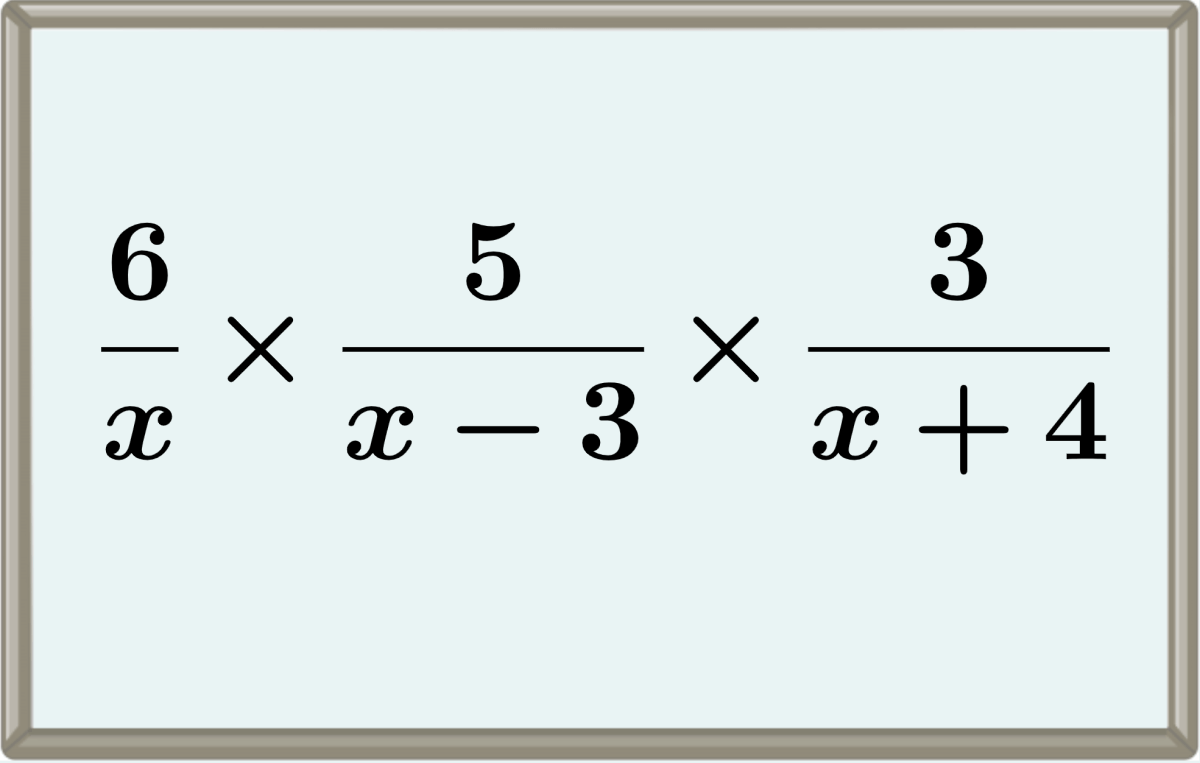
Relevante para…
Resolver ejercicios de multiplicación de fracciones algebraicas.
Cómo multiplicar dos o más fracciones algebraicas
Dos o más fracciones algebraicas pueden ser multiplicadas al multiplicar a sus numeradores y a sus denominadores separadamente.
Por ejemplo, si tenemos las fracciones $latex \frac{a}{b}$ y $latex \frac{x}{y}$, podemos multiplicarlas de la siguiente forma:
$$\frac{a}{b}\times \frac{x}{y}=\frac{a\times x}{b\times y}$$
Entonces, podemos encontrar el producto de dos o más fracciones algebraicas al seguir los siguientes pasos:
1. Multiplicar los numeradores.
2. Multiplicar los denominadores.
3. Simplificar la fracción resultante.
Eliminamos los factores comunes en el numerador y denominador.
Ejercicios resueltos de producto de fracciones algebraicas
EJERCICIO 1
Multiplique las siguientes fracciones algebraicas:
$$ \frac{2a}{3b^3} \times \frac{3b^2}{4a}$$
Solución
La fracción resultante del producto (o multiplicación) de dos fracciones algebraicas, es el producto de los numeradores dividido entre la multiplicación de sus denominadores:
$$ \frac{2a}{3b^3} \cdot \frac{3b^2}{4a} = \frac{(2a)\cdot (3b^2)}{(3b^3) \cdot (4a)}$$
Simplificando los factores semejantes en numerador y denominador nos queda:
$$ =\frac{(1) \cdot (1)}{(b) \cdot (2)} $$
El resultado final es:
$$ \frac{1}{2b} $$
EJERCICIO 2
Encuentre el resultado del siguiente producto de fracciones algebraicas:
$$ \frac{7x+7}{10x+50} \cdot \frac{5x+25}{14} $$
Solución
Factorizamos numerador y denominador de cada una de las fracciones indicadas:
$$ \frac{7(x+1)}{10(x+5)} \cdot \frac{5(x+5)}{2 \cdot 7} $$
Multiplicamos numerador por numerador y denominador por denominador:
$$ \frac{7(x+1) \cdot 5(x+5)}{10(x+5) \cdot 2 \cdot 7} $$
Simplificamos o cancelamos factores semejantes entre el numerador y el denominador:
$$ \frac{(x+1)}{2 \cdot 2 } $$
El resultado final es:
$$ \frac{(x+1)}{4} $$
EJERCICIO 3
Simplificar lo mas posible el siguiente producto de tres fracciones algebraicas:
$$ \frac{10}{a} \cdot \frac{2a}{b^2} \cdot \frac{3b}{20} $$
Solución
Multiplicamos numeradores entre si y denominadores entre si:
$$ \frac{10 \cdot 2a \cdot 3b}{a \cdot b^2 \cdot 20} $$
Simplificamos:
$$ \frac{1 \cdot 2 \cdot 3}{1 \cdot b \cdot 2} = \frac{1 \cdot 1 \cdot 3}{1 \cdot b \cdot 1} $$
El resultado final es:
$$ \frac{3}{b} $$
EJERCICIO 4
Efectuar el siguiente producto de fracciones:
$$ \frac{x^3 + 2x^2 + x}{a^2 – b^2} \cdot \frac{a – b}{x^2 + x} $$
Solución
Se multiplican numeradores y denominadores entre si:
$$ \frac{(x^3 + 2x^2 + x)(a – b)}{(a^2 – b^2)(x^2 + x)} $$
Se factoriza lo mas posible numerador y denominador:
$$ =\frac{x(x^2 + 2x + 1)(a – b)}{(a^2 – b^2)(x + 1)x} $$
Podemos factorizar la expresión $latex x^2+2x+1$ reconociendo que esto es igual a $latex (x+1)^2$:
$$ =\frac{x(x+1)^2(a – b)}{(a^2 – b^2)(x + 1)x} $$
Teniendo en cuenta que una diferencia de cuadrados es el producto de la suma por la diferencia nos queda:
$$ =\frac{x(x+1)^2(a – b)}{(a + b)(a – b)(x + 1)x} $$
Ahora simplificamos o cancelamos factores semejantes entre numerador y denominador:
$$ =\frac{1(x+1)(1)}{(a + b)(1)(1)1} $$
Finalmente nos queda:
$$ \frac{(x+1)}{(a + b)} $$
EJERCICIO 5
Hallar la solución del siguiente producto de fracciones algebraicas:
$$ \frac{a^2-4a – 5}{2a^2-50} \cdot \frac{2a-2}{3a+3} $$
Solución
Multiplicamos numeradores entre si y denominadores entre si:
$$ \frac{(a^2-4a – 5)(2a-2)}{(2a^2-50)(3a+3)} $$
Sustituimos el primer factor del numerador que es un polinomio cuadrático por el producto de dos binomios:
$$ (a^2-4a – 5) = (a-5)(a+1) $$
y sacamos factor común donde sea posible:
$$ \frac{(a-5)(a+1)2(a-1)}{(2(a^2-25))3(a+1)} $$
Aplicamos la fórmula de la diferencia de cuadrados en $latex (a^2-25)$:
$$ \frac{(a-5)(a+1)2(a-1)}{(2(a – 5)(a+5))3(a+1)} $$
Simplificamos
$$ \frac{(a-1)}{(a+5)3} $$
El resultado final es:
$$ \frac{(a-1)}{3(a+5)} $$
EJERCICIO 6
Determine el resultado de multiplicar las expresiones algebraicas que se muestran a continuación. Se sugiere reducirlas primero a fracciones algebraicas y luego multiplicar:
$$ (1 + \frac{a}{b})(a – \frac{a^2}{a+b}) $$
Solución
La expresión dada es equivalente a:
$$ ( \frac{1}{1} + \frac{a}{b})( \frac{a}{1} – \frac{a^2}{a+b}) $$
En primer lugar se suman y se restan las fracciones en cada una de las expresiones entre los paréntesis:
$$ (\frac{b+a}{b})( \frac{a^2 + ab -a^2}{a+b}) $$
Simplificando nos queda:
$$ (\frac{b+a}{b})( \frac{ ab }{a+b}) $$
Ahora multiplicamos las fracciones de la forma habitual, numerador por numerador y denominador por denominador:
$$ \frac{(b+a)ab}{b(a+b)} $$
Después de simplificar, es decir cancelar factores iguales en numerador y denominador, nos queda que la respuesta final es:
$$ a $$
EJERCICIO 7
Reducir las expresiones entre paréntesis a la forma de fracción algebraica y luego efectuar la multiplicación de las mismas
$$ (x – \frac{x}{y+1})( x + \frac{x}{y}) $$
Solución
Tomando en cuenta que $latex x = \frac{x}{1} $ se efectúa la resta de fracciones en el primer paréntesis y la suma en el segundo:
$$ (\frac{x(y+1) -x}{y+1})( \frac{xy + x}{y}) $$
Desarrollamos el primer numerador y sacamos factor común x en el segundo numerador:
$$ (\frac{xy+x -x}{y+1})( \frac{x(y + 1)}{y}) $$
Simplificamos:
$$ (\frac{xy}{y+1})( \frac{x(y + 1)}{y}) $$
Multiplicamos las fracciones que están entre paréntesis:
$$ \frac{x^2y(y+1)}{(y+1)y} $$
Se cancelan los factores iguales entre numerador y denominador, quedando como resultado final:
$$ x^2 $$
EJERCICIO 8
Resolver el producto de las tres fracciones algebraicas que se muestran a continuación:
$$ \frac{5}{x} \cdot \frac{2x}{b^2} \cdot \frac{3b}{10} $$
Solución
Multiplicamos numeradores entre sí y denominadores entre sí:
$$ \frac{30xb}{10xb^2} $$
Después de simplificar se obtiene que la respuesta es:
$$ \frac{3}{b} $$
EJERCICIO 9
Resolver lo siguiente:
$$ (1+\frac{x}{y})(1- \frac{x}{y}) $$
Solución
Tenemos el producto de una suma por una diferencia, que es igual a una diferencia de cuadrados:
$$ 1^2-(\frac{x}{y})^2 $$
En la expresión anterior tenemos una fracción algebraica elevada al cuadrado, lo que equivale a multiplicar la fracción por sí misma:
$$ \frac{1}{1}-\frac{x^2}{y^2} $$
Se resuelve la resta de fracciones algebraicas y nos queda:
$$ \frac{y^2-x^2}{y^2} $$
Factorizamos el numerador usando nuevamente el producto notable de la diferencia de cuadrados, para obtener como resultado final:
$$ \frac{(y-x)(x+y)}{y^2} $$
EJERCICIO 10
Multiplicar:
$$ (\frac{15x^3 + 15x^2}{20x^2-30x})(\frac{4x-6}{x+1}) $$
Solución
Antes de efectuar la multiplicación se saca factor común en numeradores y denominadores:
$$ \frac{15x^2(x + 1)}{10x(2x-3)} \cdot \frac{2(2x-3)}{x+1} $$
Se multiplican las fracciones:
$$ \frac{30x^2(x + 1)(2x-3)}{10x(2x-3)(x+1)} $$
Cancelando los factores iguales entre numerador y denominador se tiene el resultado final:
$$ \frac{3x}{1} = 3x $$
Ejercicios de producto de fracciones algebraicas para resolver


¿Cuál es el resultado al multiplicar las fracciones y simplificar? $$\frac{5x^2}{x^2-2x} \cdot \frac{x^2-4}{x^2+2x} $$
Escribe el resultado en la casilla.
Véase también
¿Interesado en aprender más sobre fracciones algebraicas? Puedes mirar estas páginas:


