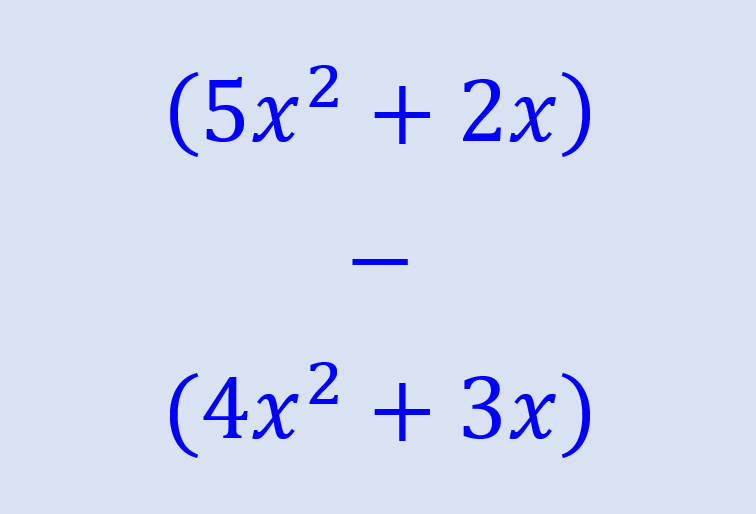La resta de polinomios es una de las operaciones matemáticas más fáciles que podemos realizar con polinomios. Para realizar una resta de polinomios, tenemos que identificar los términos semejantes y restar los coeficientes de los términos semejantes.
A continuación, veremos un resumen de la resta de polinomios y el proceso usado. Además, veremos varios ejercicios de resta de polinomios resueltos para dominar completamente este tema.
Resumen de resta de polinomios
Para restar dos o más polinomios, solo tenemos que combinar términos semejantes y considerar el orden de las operaciones. Algo importante que debe ser tomado en cuenta es distinguir los términos con signos “más” y “menos” en cada polinomio.
Seguimos los siguientes pasos para restar polinomios:
Paso 1: Eliminar todos los paréntesis. Para facilitar la visualización, es recomendable escribir el problema y cada proceso de forma vertical. Cuando eliminamos los paréntesis, tenemos que distribuir el signo negativo, lo cual hará que cada uno de los términos cambie de signo.
Paso 2: Combinar términos semejantes. Si es que escribimos los pasos de forma vertical, la combinación de términos semejantes resulta más fácil. Recuerda que, los términos semejantes son términos que tienen las mismas variables con los mismos exponentes.
Ejercicios de resta de polinomios resueltos
Usa los siguientes ejercicios para dominar el tema de resta de polinomios. Cada ejercicio tiene una solución detallada que indica el razonamiento usado para obtener la respuesta. Es recomendable que intentes resolver los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
Realiza la sustracción de polinomios: $latex (6x+8y)-(3x-2y)$.
Solución
Tenemos que eliminar los paréntesis. Para realizar esto, tenemos que tomar en cuenta el signo negativo en frente del segundo polinomio, por lo que cambiamos de signo a todos los términos del segundo polinomio.
Luego, tenemos que agrupar términos semejantes:
$latex (6x+8y)-(3x-2y)$
$latex =6x+8y-3x+2y$
$latex =6x-3x+8y+2y$
$latex =3x+10y$
Estos términos ya no son semejantes, ya que no tienen la misma variable, por lo que no podemos combinarlos.
EJERCICIO 2
Resuelve la resta $latex (6x+8y)-(3x-2y)$ verticalmente.
Solución
Podemos restar polinomios verticalmente al colocar a cada variable en su propia columna. Entonces, usamos la primera columna para la x y la segunda para la y.
Dado que estamos restando el segundo polinomio, tenemos que cambiar de signo a todos sus términos
$latex 6x+8y$
$latex -3x+2y$
______________
$latex 3x+10y$
Claramente, obtuvimos la misma respuesta que cuando restamos horizontalmente. Es posible resolver la resta de polinomios usando cualquier formato. Solo elige el formato con el que más te sientas a gusto.
Generalmente, cuando tenemos polinomios simples, el formato horizontal resulta más fácil. Sin embargo, para los polinomios más largos y complicados, restar verticalmente puede facilitar el proceso.
EJERCICIO 3
Realiza la resta de polinomios: $latex (4{{x}^3}+2{{x}^2}-4x+6)$ $latex -(2{{x}^3}+4{{x}^2}+6x-7)$.
Solución
Podemos empezar realizando la resta horizontalmente. Entonces, eliminamos los paréntesis teniendo en cuenta el signo “menos” y luego, combinamos términos semejantes:
$latex (4{{x}^3}+2{{x}^2}-4x+6)$ $latex -(2{{x}^3}+4{{x}^2}+6x-7)$
$latex =4{{x}^3}+2{{x}^2}-4x+6$ $latex -2{{x}^3}-4{{x}^2}-6x+7$
$latex =4{{x}^3}-2{{x}^3}+2{{x}^2}-4{{x}^2}$ $latex -4x-6x+6+7$
$latex =2{{x}^3}-2{{x}^2}-10x+13$
Ahora, podemos realizar la resta verticalmente. Separamos por columnas a cada exponente y cambiamos de signo a todos los términos del segundo polinomio, ya que tenemos al signo “menos” en frente:
$latex 4{{x}^3}+2{{x}^2}-4x+6$
$latex -2{{x}^3}-4{{x}^2}-6x+7$
_____________________
$latex 2{{x}^3}-2{{x}^2}-10x+13$
EJERCICIO 4
Resuelve la resta $$ (-5{{x}^3}+6{{x}^2}-4x)-(3{{x}^3}-5{{x}^2}-6x)$$.
Solución
Vamos a realizar la resta horizontalmente. Entonces, eliminamos los paréntesis cambiando los signos de los términos del segundo polinomio, ya que tienen al signo “menos” en frente. Luego, simplificamos al combinar términos semejantes:
$$(-5{{x}^3}+6{{x}^2}-4x)-(3{{x}^3}-5{{x}^2}-6x)$$
$$=-5{{x}^3}+6{{x}^2}-4x-3{{x}^3}+5{{x}^2}+6x$$
$$=-5{{x}^3}-3{{x}^3}+6{{x}^2}+5{{x}^2}-4x+6x$$
$latex =-8{{x}^3}+11{{x}^2}+2x$
Ahora, realizamos la resta verticalmente. Tenemos que asignar una columna a cada exponente y tenemos que cambiar de signo a los términos del segundo polinomio:
$latex -5{{x}^3}+6{{x}^2}-4x$
$latex -3{{x}^3}+5{{x}^2}+6x$
__________________
$latex -8{{x}^3}+11{{x}^2}+2x$
EJERCICIO 5
Resuelve la siguiente operación: $latex (4{{x}^2}+2x-5)-(5{{x}^2}-4x-4)$ $latex -(-6{{x}^2}+3x+10)$.
Solución
En este caso, resultará más fácil si resolvemos la resta de polinomios usando el formato vertical.
Separamos las variables en diferentes columnas dependiendo el exponente y cambiamos de signo a todos los términos de los polinomios que están siendo restados:
$latex 4{{x}^2}+2x-5$
$latex -5{{x}^2}+4x+4$
$latex 6{{x}^2}-3x-10$
___________________
$latex 5{{x}^2}+3x-11$
Ejercicios de resta de polinomios para resolver
Practica la resta de polinomios con los siguientes ejercicios. Resuelve las restas y escoge tu respuesta. Haz clic en “Verificar” para comprobar que seleccionaste la respuesta correcta.
Véase también
¿Interesado en aprender más sobre operaciones de polinomios? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
