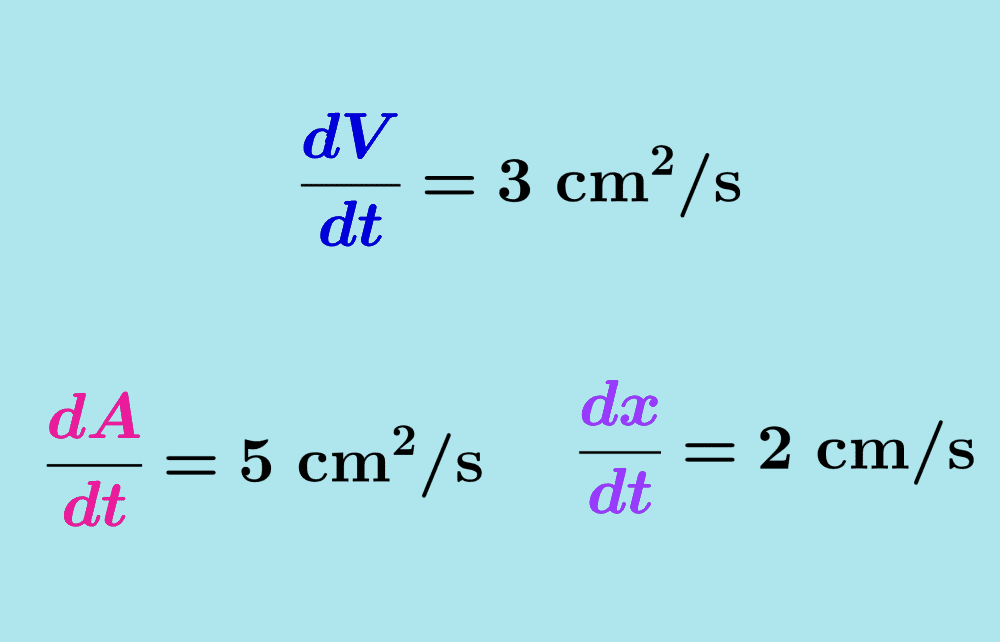Los ejercicios de razón de cambio son resueltos al encontrar la derivada de una ecuación con respecto a la variable principal. Generalmente, la regla de la cadena es usada para encontrar la razón de cambio requerida.
A continuación, veremos varios ejercicios resueltos de razón de cambio usando derivadas. Luego, veremos algunos ejercicios de práctica para aplicar lo aprendido.
¿Qué es la razón de cambio en cálculo?
La razón de cambio representa la relación entre los cambios de la variable dependiente en comparación con los cambios de la variable independiente.
La siguiente derivada
$$\dfrac{dy}{dx}=\lim_{\delta \to 0} \frac{\delta y }{\delta x}$$
es la razón de cambio de $latex y $ con respecto a $latex x$.
Esta razón de cambio muestra cómo los cambios en $latex y$ están relacionados con los cambios de $latex x$. Por ejemplo, si es que $latex \dfrac{dy}{dy}=5$, entonces, $latex y$ incrementa 5 veces más rápido que $latex x$.
Frecuentemente, otras letras además de $latex x$ y $latex y$ son usadas. Por ejemplo, en física es común usar $latex s$ para indicar la posición de un objeto. Entonces:
- $latex \dfrac{ds}{dt}$ es la velocidad, ya que representa la razón de cambio del desplazamiento con respecto al tiempo.
- $latex \dfrac{d^2s}{dt^2}$ es la aceleración porque representa la razón de cambio de la velocidad con respecto al tiempo.
Muchas situaciones prácticas involucran razones de cambio relacionadas con el uso de la regla de la cadena de derivadas, como se muestra en los siguientes ejemplos.
Ejercicios resueltos de razón de cambio con derivadas
EJERCICIO 1
El lado de una pieza cuadrada de metal incrementa a una razón de 0.1 cm por segundo cuando es calentada. ¿Cuál es la razón de cambio del área de la superficie cuadrada del metal?
Solución
Para resolver este problema, tenemos que empezar por encontrar una ecuación para el área de la pieza cuadrada de metal.
Si es que representamos a los lados de la pieza de metal con $latex x$, su área es $latex A=x^2$.
Tenemos que la razón de cambio de la longitud de un lado con respecto al tiempo, es decir, $latex \dfrac{dx}{dt}$, es 0.1 cm/s.
Queremos encontrar la razón de cambio del área con respecto al tiempo, es decir, $latex \dfrac{dA}{dt}$.
Si es que derivamos $latex A=x^2$, tenemos $latex \dfrac{dA}{dx}=2x$. Además, dado que $latex \dfrac{dx}{dt}=0.1$, podemos usar la regla de la cadena:
$$\dfrac{dA}{dt}=\dfrac{dA}{dx}\dfrac{dx}{dt}$$
$latex =2x \times 0.1$
$$\dfrac{dA}{dt}=0.2x$$
La razón de cambio del área es $latex 0.2x$ cm2/s.
EJERCICIO 2
El lado de un cuadrado está incrementando a una razón de 5 cm/s. Encuentra la razón de cambio del área cuando la longitud de un lado es 10 cm.
Solución
Nuevamente, empezamos encontrando una ecuación para el área del cuadrado en término de sus lados.
Si es que representamos a los lados del cuadrado con $latex x$, su área es $latex A=x^2$.
De la pregunta, conocemos la razón de cambio de la longitud de un lado con respecto al tiempo, es decir, $latex \dfrac{dx}{dt}=$5 cm/s.
Para encontrar la razón de cambio del área, es decir, $latex \dfrac{dA}{dt}$, derivamos $latex A=x^2$ y usamos la regla de la cadena:
$$\dfrac{dA}{dt}=\dfrac{dA}{dx}\dfrac{dx}{dt}$$
$latex =2x \times 5$
$$\dfrac{dA}{dt}=10x$$
Cuando la longitud de un lado es 10 cm, la razón de cambio del área del cuadrado es $latex 10(10)=100$ cm2/s.
EJERCICIO 3
El radio de un círculo está incrementando a una razón de $latex \frac{1}{3}$ cm/s. Encuentra la razón de cambio del área cuando el radio es 5 cm.
Solución
En este caso, tenemos un círculo. La ecuación del área con respecto al radio del círculo es $latex A=\pi r^2$.
Si es que derivamos a $latex A=\pi r^2$ con respecto al radio, tenemos $latex \dfrac{dA}{dr}=2\pi r$.
Ahora, de la pregunta, sabemos que la razón de cambio del radio del círculo con respecto al tiempo, es decir, $latex \dfrac{dr}{dt}$, es $latex \frac{1}{3}$ cm/s.
Entonces, para encontrar la razón de cambio del área con respecto al tiempo, es decir, $latex \dfrac{dA}{dt}$, podemos usar la regla de la cadena:
$$\dfrac{dA}{dt}=\dfrac{dA}{dr}\dfrac{dr}{dt}$$
$latex =2\pi r \times \frac{1}{3}$
$$\dfrac{dA}{dt}=\frac{2\pi r}{3}$$
Cuando el radio es 5 cm, la razón de cambio del área del círculo es $latex \frac{2\pi (5)}{3}=\frac{10\pi}{3}$ cm2/s.
EJERCICIO 4
El área de un cuadrado está incrementando a una razón de 7 cm2/s. Encuentra la razón de cambio de la longitud de un lado cuando el área es 100 cm2.
Solución
Como ya sabemos, el área de un cuadrado con respecto a sus lados puede ser representado por la ecuación $latex A=x^2$, en donde, x es un lado.
Ahora, resolviendo para $latex x$, tenemos $latex x=\sqrt{A}$. Cuando derivamos, tenemos $latex \dfrac{dx}{dA}=\frac{1}{2\sqrt{A}}$.
En este caso, tenemos que la razón de cambio del área del cuadrado con respecto al tiempo, es decir, $latex \dfrac{dA}{dt}$, es 7 cm2/s.
Entonces, encontramos la razón de cambio de la longitud de un lado con respecto al tiempo, es decir, $latex \dfrac{dx}{dt}$, usando la regla de la cadena:
$$\dfrac{dx}{dt}=\dfrac{dA}{dt}\dfrac{dx}{dA}$$
$$=7 \times \frac{1}{2\sqrt{A}}$$
$$\dfrac{dx}{dt}=\frac{7}{2\sqrt{A}}$$
Cuando el área es 100 cm2, la razón de cambio de un lado del cuadrado es $latex \frac{7}{2\sqrt{100}}=\frac{7}{20}$ cm/s.
EJERCICIO 5
El área de un círculo está incrementando a una razón de (4π) cm2/s. Encuentra la razón de cambio del radio cuando este radio es $latex \frac{1}{2}$ cm.
Solución
Podemos representar al área de un círculo con respecto al radio con la ecuación $latex A=\pi r^2$.
Cuando derivamos a esta ecuación con respecto a $latex r$, tenemos $latex \dfrac{dA}{dr}=2 \pi r$.
Tenemos que la razón de cambio del área del círculo con respecto al tiempo, es decir, $latex \dfrac{dA}{dt}$, es (4π) cm2/s.
Ahora, para encontrar la razón de cambio del radio con respecto al tiempo, es decir, $latex \dfrac{dr}{dt}$, usamos la regla de la cadena:
$$\dfrac{dr}{dt}=\dfrac{dA}{dt}\dfrac{dr}{dA}$$
Observamos que $latex \dfrac{dr}{dA}$ es el recíproco de $latex \dfrac{dA}{dr}. Entonces, tenemos:
$$\dfrac{dr}{dt}=4\pi \times \dfrac{1}{2 \pi r}$$
$$\dfrac{dr}{dt}=\frac{2}{r}$$
Cuando el radio es $latex \frac{1}{2}$ cm, la razón de cambio del radio del círculo es $latex \frac{2}{\frac{1}{2}}=4$ cm/s.
EJERCICIO 6
El volumen de un cubo está incrementando a una razón de 18 cm3/s. Encuentra la razón de cambio de la longitud de un lado cuando el volumen es 125 cm3.
Solución
Si es que usamos $latex x$ para representar a los lados del cubo, su volumen es $latex V=x^3$.
Resolviendo para $latex x$, tenemos $latex x=\sqrt[3]{V}$. Derivando, tenemos $latex \dfrac{dx}{dV}=\frac{1}{3\sqrt[3]{V}}$.
Dado que la pregunta nos dice que el volumen del cubo incrementa a una razón de 18 cm3/s, tenemos $latex \dfrac{dV}{dt}=18$ cm3/s.
Entonces, encontramos la razón de cambio de un lado del cubo con respecto al tiempo, $latex \dfrac{dx}{dt}$, aplicando la regla de la cadena:
$$\dfrac{dx}{dt}=\dfrac{dV}{dt}\dfrac{dx}{dV}$$
$latex =18 \times \frac{1}{3\sqrt[3]{V}}$
$$\dfrac{dA}{dt}=\frac{18}{3\sqrt[3]{V}}$$
Cuando el volumen es 125 cm3, la razón de cambio de un lado del cubo es $latex \frac{18}{3\sqrt[3]{125}}=\frac{6}{25}$ cm/s.
EJERCICIO 7
Un globo completamente esférico está siendo inflado a una razón de 3 cm3/s. Encuentra la razón de cambio del radio cuando el radio es 2 cm.
Solución
Si es que representamos al radio por $latex r$ y al volumen por $latex V$, tenemos $latex V=\frac{4}{3}\pi r^3$. Entonces, su derivada es:
$$\dfrac{dV}{dr}=4\pi r^2$$
De la pregunta, tenemos $latex \dfrac{dV}{dt}=3$. Entonces, usando la regla de la cadena, tenemos:
$$\dfrac{dV}{dt}=\dfrac{dV}{dr}\dfrac{dr}{dt}$$
$$3=4\pi r^2 \times \dfrac{dr}{dt}$$
$$\dfrac{dr}{dt}=\frac{3}{4\pi r^2}$$
Cuando $latex r=2$, tenemos:
$$\frac{dr}{dt}\Big|_{r=2}=\frac{3}{4\pi (2)^2}=\frac{3}{16\pi}$$
La razón de cambio del radio cuando el radio es 2 cm es $latex \frac{3}{16\pi}$ cm/s.
EJERCICIO 8
El área superficial de una esfera está incrementando a una razón de 2 cm2/s. Encuentra la razón de cambio del radio cuando el área superficial es (100π) cm2.
Solución
Cuando representamos al radio por $latex r$ y al área superficial por $latex A_{s}$, tenemos $latex A_{s}=4\pi r^2$.
Dado que conocemos el área superficial, tenemos que escribir a una ecuación de $latex r$ con respecto a A: $latex r=\sqrt{\frac{A_{s}}{4\pi}}$. Su derivada es:
$$\dfrac{dr}{dA_{s}}=\frac{1}{4\sqrt{\pi A_{s}}}$$
Tenemos la información $latex \dfrac{dA_{s}}{dt}=2$. Entonces, al aplicar la regla de la cadena, tenemos:
$$\dfrac{dr}{dt}=\dfrac{dA_{s}}{dt}\dfrac{dr}{dA_{s}}$$
$$=2 \times \frac{1}{4\sqrt{\pi A_{s}} }$$
$$\dfrac{dr}{dt}=\frac{1}{2\sqrt{\pi A_{s}}}$$
Cuando $latex A_{s}=100\pi$, tenemos:
$$\frac{dr}{dt}\Big|_{A_{s}=2}=\frac{1}{2\sqrt{100\pi^2}}=\frac{1}{20\pi}$$
La razón de cambio del radio cuando el área superficial es 100π es $latex \frac{1}{20\pi}$ cm/s.
EJERCICIO 9
Un globo esférico está siendo inflado a una razón de 10 cm3/s. Encuentra la razón de cambio del área superficial cuando el radio es 5 cm.
Solución
Al representar al radio por $latex r$ y al área superficial por $latex A_{s}$, tenemos $latex V=\frac{4}{3}\pi r^3$ y $latex A_{s}=4\pi r^2$. Entonces, sus derivadas son:
$$\dfrac{dV}{dr}=4\pi r^2$$
$$\dfrac{dA_{s}}{dr}=8\pi r$$
Sabemos que $latex \dfrac{dV}{dt}=10$. Entonces, usando la regla de la cadena, tenemos:
$$\dfrac{dA_{s}}{dt}=\dfrac{dV}{dt}\dfrac{dA_{s}}{dr}\dfrac{dr}{dV}$$
$$=10 \times 8\pi r \times \frac{1}{4\pi r^2}$$
$$\dfrac{dA_{s}}{dt}=\frac{20}{r}$$
Cuando $latex r=5$, tenemos:
$$\frac{dA_{s}}{dt}\Big|_{r=5}=\frac{20}{5}=4$$
La razón de cambio del área superficial cuando el radio es 5 cm es 4 cm2/s.
EJERCICIO 10
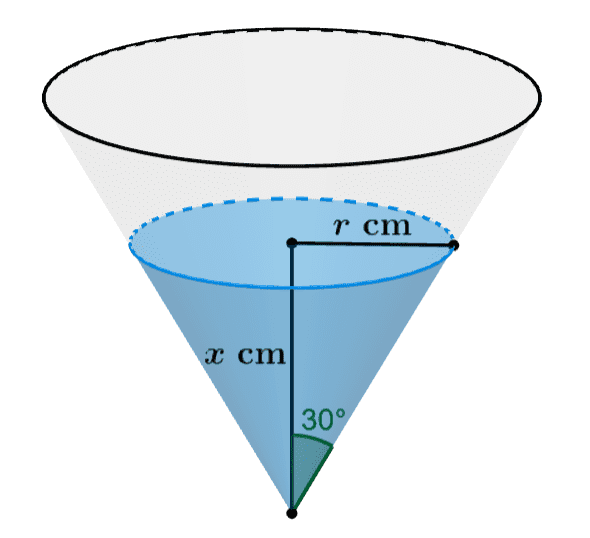
Un contenedor tiene la forma de un cono hueco con un ángulo semi-vertical de 30° y su vértice apunta hacia abajo.
Si es que el agua es vertida en el cono a una razón de 5 cm3/s, encuentra la razón a la cual la profundidad del agua en el cono está incrementando cuando su profundidad es 10 cm.
Solución
Podemos usar el siguiente diagrama para facilitar la resolución:
La profundidad del agua en el cono es representada por $latex x$. Entonces, el radio $latex r$ de la sección transversal del agua está dado por:
$$\tan(30^{\circ})=\frac{r}{x}$$
$$r=x\tan(30^{\circ})$$
$$=\frac{x}{\sqrt{3}}$$
El volumen del agua en el cono está dado por:
$$V=\frac{1}{3}\pi r^2x$$
$$=\frac{1}{3}\pi \left(\frac{x}{\sqrt{3}}\right)^2x$$
$$=\frac{1}{9}\pi x^3$$
Entonces, la derivada del volumen con respecto a $latex x$ es:
$$\dfrac{dV}{dx}\pi x^2$$
De la pregunta, sabemos que $latex \dfrac{dV}{dt}=5$. Además, por la regla de la cadena, tenemos:
$$\dfrac{dV}{dt}=\dfrac{dV}{dx} \dfrac{dx}{dt}$$
Entonces,
$$ 5= \frac{1}{3}\pi x^2 \dfrac{dx}{dt}$$
$$ \dfrac{dx}{dt}= \frac{15}{\pi x^2}$$
Cuando $latex x=10$, tenemos:
$$\dfrac{dx}{dt}=\frac{15}{\pi (10)^2}=\frac{3}{20\pi}$$
La razón de cambio de la profundidad cuando la profundidad es 10 cm es $latex \frac{3}{20\pi}$ cm/s.
Ejercicios de razón de cambio con derivadas para resolver
Un cono hueco con una base de radio 10 cm y una altura de 10 cm tiene su vértice apuntando hacia abajo.
El cono está vacío inicialmente cuando agua es vertida a una razón de 4π cm3/s. Encuentra la razón a la que la profundidad de agua incrementa a 18 segundos de que se empezó a llenar.
Escribe la respuesta en la casilla.
Véase también
¿Interesado en aprender más sobre derivadas? Puedes mirar estas páginas: