La función exponencial es una de las funciones más importantes en matemáticas. Para formar una función exponencial, hacemos que la variable independiente sea el exponente. Estas funciones son usadas en muchas situaciones de la vida real. Principalmente, son usadas para el crecimiento poblacional, interés compuesto o radioactividad.
A continuación, veremos un resumen de las funciones exponenciales. También, exploraremos varios ejercicios de funciones exponenciales resueltos para entender el uso de estas funciones.
Resumen de funciones exponenciales
Una función exponencial es una función matemática que tiene la forma general $latex f(x)={{b}^x}$, en donde x es una variable y b es una constante llamada la base de la función y debe ser mayor que 0. En las funciones exponenciales, la variable de entrada, x, ocurre como un exponente.
Las siguientes son las propiedades de la función exponencial estándar $latex f(x)={{b}^x}$:
1. La gráfica de $latex f(x)$ siempre contendrá el punto (0, 1). Esto es equivalente a tener $latex f(0)=1$ independientemente del valor de b.
2. Para cualquier valor posible de b, tenemos $latex {{b}^x}>0$. Esto implica que $latex {{b}^x}$ es diferente de cero.
3. Si es que tenemos $latex 0<b<1$, entonces, la gráfica de $latex f(x)={{b}^x}$ decrecerá de izquierda a derecha.
4. Si es que tenemos $latex b>1$, entonces, la gráfica de $latex f(x)={{b}^x}$ crecerá de izquierda a derecha.
5. Si es que tenemos $latex {{b}^x}={{b}^y}$, esto significa que $latex x=y$.
Ejercicios de funciones exponenciales resueltos
Los siguientes ejercicios usan algunas de las aplicaciones de las funciones exponenciales. Cada uno de los ejercicios tiene su respectiva solución que puede ser útil para entender el proceso y el razonamiento usados.
EJERCICIO 1
Dada la función $latex f(x)={{2}^x}$, encuentra $latex f(-2)$.
Solución
Para evaluar cualquier función, simplemente tenemos que usar la entrada dada. Entonces, tenemos:
$latex f(-2)={{2}^{-2}}$
$latex =\frac{1}{{{2}^2}}$
$latex =\frac{1}{4}$
EJERCICIO 2
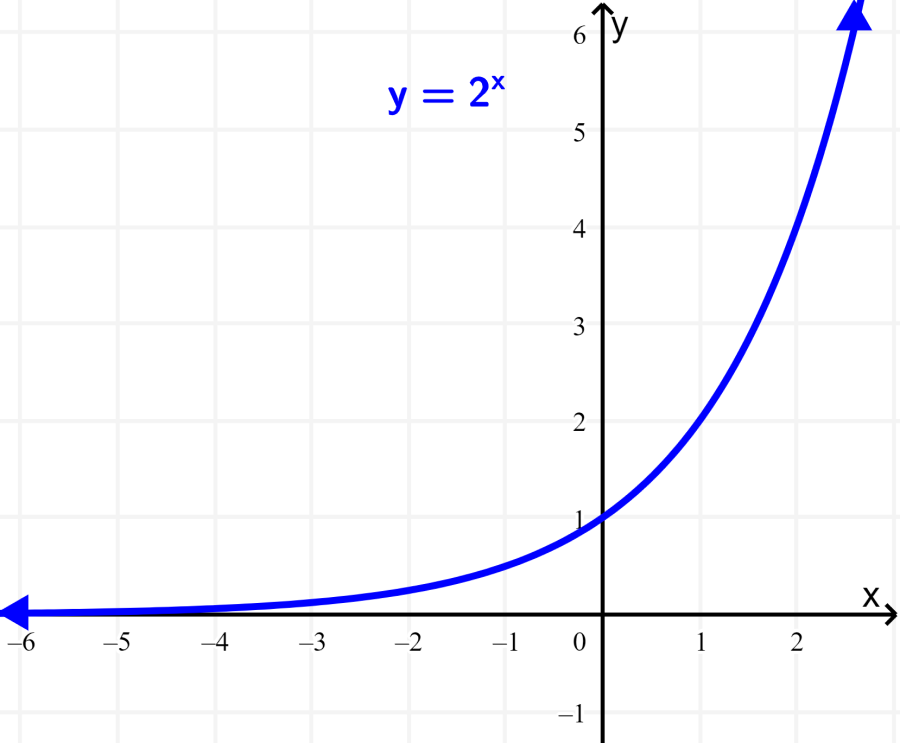
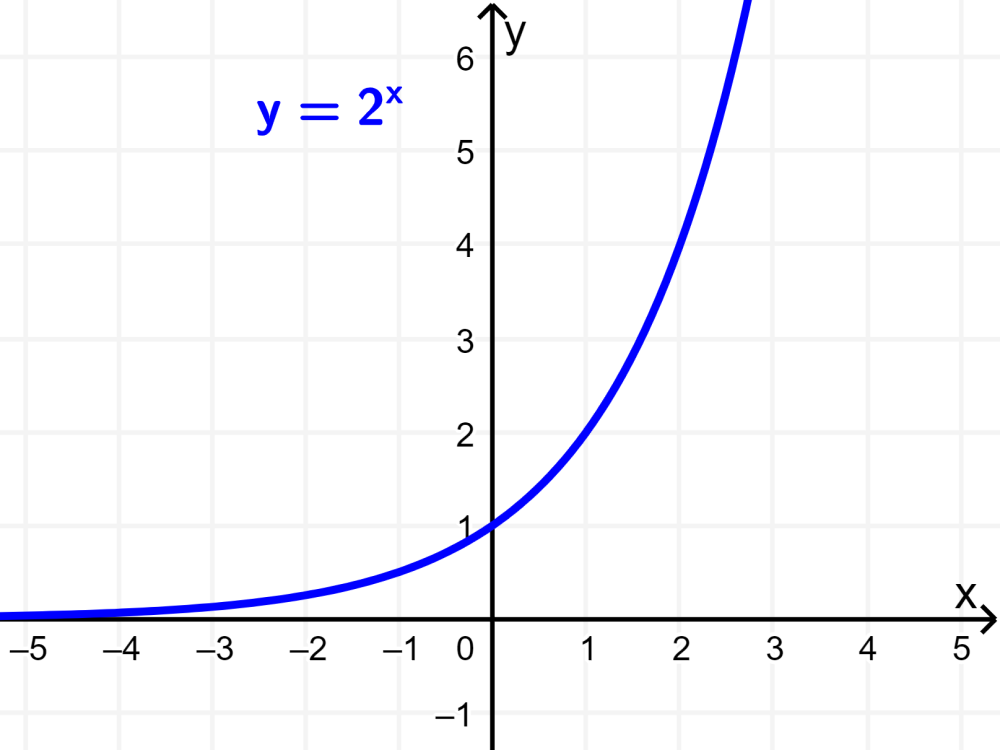
Grafica la función $latex f(x)={{2}^x}$.
Solución
Para graficar una función, podemos usar varios valores de x para encontrar puntos que se ubiquen en la gráfica. Sabemos que todas las funciones exponenciales pasan por el punto (0, 1), por lo que ya tenemos un punto.
Adicionalmente, podemos usar los valores $latex x=-1$, $latex x=-2$, $latex x=1$ y $latex x=2$:
- Cuando $latex x=-1$, tenemos $latex f(-1)={{2}^{-1}}=\frac{1}{2}$.
- Cuando $latex x=-2$, tenemos $latex f(-2)={{2}^{-2}}=\frac{1}{4}$.
- Cuando $latex x=1$, tenemos $latex f(1)={{2}^1}=2$.
- Cuando $latex x=2$, tenemos $latex f(2)={{2}^2}=4$.
Trazando estos puntos y graficando la curva, tenemos lo siguiente:
EJERCICIO 3
La población de una cierta región puede ser modelada con la fórmula $latex A=10000({{e}^{0.005t}})$, en donde A representa a la población y t representa el tiempo en años. Encuentra la población al final de 10 años.
Solución
Este es un ejemplo del uso de funciones exponenciales para modelar el crecimiento poblacional. Tenemos la función $latex A=10000({{e}^{0.005t}})$ y tenemos el tiempo $latex t=10$. Reemplazando $latex t=10$, tenemos:
$latex A=10000({{e}^{0.005(10)}})$
$latex =10000({{e}^{0.05}})$
$latex =10000(1.0513)$
$latex =10513$
Entonces, la población de la región después de 10 años será 10513.
EJERCICIO 4
En el año 1950, la población de una ciudad era 10000. Veinte años después, se encontró que la población era 20000. Encuentra la función exponencial que modela a la población P después de que t años han pasado.
Solución
Sabemos que la función exponencial que modela al crecimiento poblacional tiene la forma general $latex P=N({{e}^{\lambda t}})$, en donde N es la población inicial, λ es una constante y t es el tiempo.
Tenemos que encontrar la constante λ con la información dada. Entonces, tenemos:
$latex P=N({{e}^{\lambda t}})$
$latex 20000=10000({{e}^{20 \lambda}})$
$latex \frac{20000}{10000}={{e}^{20 \lambda}}$
$latex 2={{e}^{20 \lambda}}$
$latex \ln(2)=20 \lambda$
$latex \frac{\ln(2)}{20}=\lambda$
$latex 0.0347=\lambda$
La fórmula que modela este crecimiento poblacional es $latex P=10000({{e}^{0.0347 t}})$.
EJERCICIO 5
Teniendo la fórmula de crecimiento poblacional $latex P=N({{e}^{0.1234t}})$, estima cuándo la población llegará a 37500 si es que en 1950 la población fue 12500.
Solución
Con la información dada, podemos completar la fórmula de crecimiento poblacional:
$latex P=N({{e}^{0.1234t}})$
$latex 37500=12500({{e}^{0.1234t}})$
Ahora, resolvemos para el tiempo:
$latex 37500=12500({{e}^{0.1234t}})$
$latex \frac{37500}{12500}=({{e}^{0.1234t}})$
$latex 3=({{e}^{0.1234t}})$
$latex \ln(3)=0.1234t$
$latex \frac{\ln(3)}{0.1234}=t$
$latex 8.9=t$
Esto significa que la población llegará a 37500 en 1959.
EJERCICIO 6
Una cantidad de 10000 dólares son depositados en una cuenta que paga 7.5% de interés compuesto cuatro veces al año. ¿Cuánto dinero habrá en la cuenta después de 10 años?
Solución
La función exponencial usada para calcular el dinero con interés compuesto es $latex D=A{{(1+\frac{r}{n})}^{nt}}$, en donde, D es la cantidad de dinero final, A es la cantidad de dinero inicial, r es la tasa de interés en decimales, n es el número de veces que el interés es compuesto al año y t es el tiempo en años.
Usando los datos dados, tenemos:
$latex D=10000{{(1+\frac{0.075}{4})}^{4(10)}}$
$latex D=10000{{(1.01875)}^{40}}$
$latex D=21023.5$
Entonces, después de 10 años, habrá 21023.5 dólares en la cuenta.
EJERCICIO 7
Si es que tenemos 2000 dólares en una cuenta que paga el 7% de interés compuesto cuatro veces al año, ¿cuánto tiempo tomará para que la cuenta tenga 10000 dólares?
Solución
Podemos usar los dato dados para formar la función exponencial de interés compuesto:
$latex D=A{{(1+\frac{r}{n})}^{nt}}$
$latex 10000=2000{{(1+\frac{0.07}{4})}^{4t}}$
$latex 10000=2000{{(1.0175)}^{4t}}$
$latex \frac{10000}{2000}={{(1.0175)}^{4t}}$
$latex 5={{(1.0175)}^{4t}}$
$latex \ln(5)=\ln({{(1.0175)}^{4t}})$
$latex \ln(5)=4t\ln(1.0175)$
$latex \frac{\ln(5)}{\ln(1.0175)}=4t$
$latex \frac{99.77}{4}=t$
$latex 23.2=t$
Entonces, después de 23.2 años, habrá 10000 dólares en la cuenta.
→ Calculadora de Ecuaciones Exponenciales
Ejercicios de funciones exponenciales para resolver
Pon a prueba tu conocimiento sobre funciones exponenciales con los siguientes ejercicios. Resuelve los ejercicios y selecciona tu respuesta. Verifica la respuesta escogida para saber si es la correcta.
Mira los ejercicios resueltos de arriba si necesitas ayuda.
Véase también
¿Interesado en aprender más sobre funciones algebraicas? Mira estas páginas: