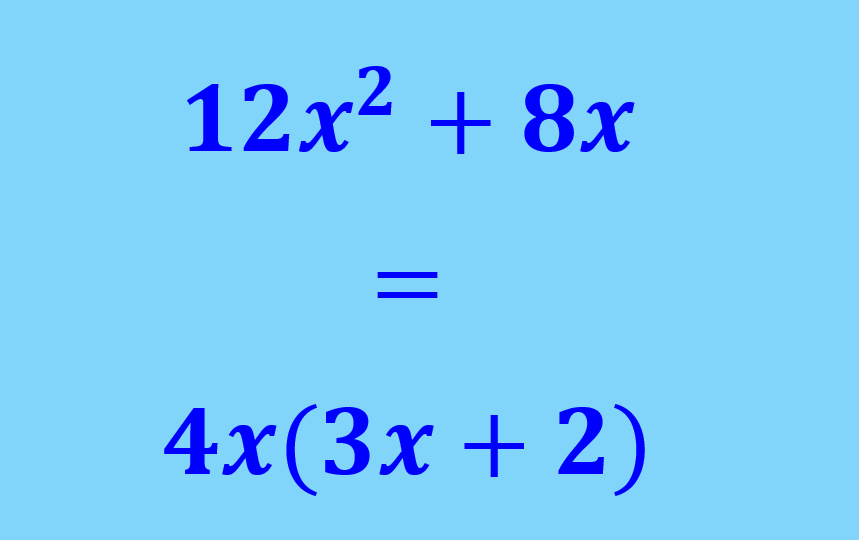Las expresiones algebraicas pueden ser factorizadas al encontrar el factor común de todos los términos. Luego de que encontremos el factor común, simplemente tenemos que escribir el factor común seguido de paréntesis. Dentro de esos paréntesis, escribimos cada término una vez que ha sido dividido por el factor común.
A continuación, miraremos un resumen del factor común y el razonamiento usado para extraer factores de expresiones algebraicas. También exploraremos varios ejercicios de factor común resueltos para dominar este concepto.
Resumen de factor común
Factorizar una expresión o un número significa escribir esa expresión o ese número como una multiplicación de factores. Entonces, factorizar es lo inverso de la multiplicación. Cuando multiplicamos, escribimos:
$latex 5(x+y)=5x+5y$
Pero, si es que factorizamos, escribimos:
$latex 5x+5y=5(x+y)$
Aquí factorizamos a $latex 5x+5y$ ya que lo escribimos como el producto $latex 5(x+y)$.
En la suma $latex 5x+5y$, 5 es un factor común de cada término. El 5 es un factor de $latex 5x$ y también un factor de $latex 5y$.
Ejercicios de factor común resueltos
Los siguientes ejercicios de factor común tienen su respectiva solución. Puedes intentar resolver los ejercicios tú mismo antes de mirar la solución.
EJERCICIO 1
Factoriza la expresión $latex 5x+5y$.
Solución
Fácilmente, podemos mirar que el 5 es un factor tanto en el término $latex 5x$ como en el término $latex 5y$. Entonces, extrayendo el 5, tenemos:
$latex 5x+5y=5(x+y)$
EJERCICIO 2
Factoriza la expresión $latex 8x-4y+12z$.
Solución
En este caso, el 4 es un factor común de todos los términos. Entonces, escribimos al 4 en la izquierda de los paréntesis:
$latex 8x-4y+12z=4(2x-x+3z)$
Para verificar la factorización, podemos multiplicar y expandir el paréntesis. Al hacer esto, deberíamos obtener la expresión original.
Ten en cuenta que, la expresión dentro del paréntesis no debe tener otros factores comunes.
EJERCICIO 3
Factoriza la expresión $latex -6a-9b-3c$.
Solución
En esta expresión, el factor común de todos los términos es -3. Entonces, lo extraímos de todos los términos:
$latex -6a-9b-3c=-3(2a+3b+c)$
EJERCICIO 4
Extrae el factor común de la expresión $latex 6{{x}^2}+9x$.
Solución
En este caso, podemos ver que el factor común de ambos términos es $latex 3x$:
$latex 6{{x}^2}+9x=3x(2x+3)$
Podemos verficar esto al multiplicar y expandir la expresión de la derecha:
$latex 3x(2x+3)=6{{x}^2}+9x$
EJERCICIO 5
Factoriza el polinomio $latex {{x}^6}+{{x}^5}+{{x}^4}+{{x}^3}$.
Solución
Este polinomio está compuesto por términos que tienen la variable x elevada a diferentes potencias.
Entonces, encontramos la potencia más pequeña en los términos y la extraemos. En este caso, la potencia más pequeña es el 3:
$${{x}^6}+{{x}^5}+{{x}^4}+{{x}^3}={{x}^3}({{x}^3}+{{x}^2}+{{x}^1}+1)$$
EJERCICIO 6
Factoriza la expresión $latex 3{{x}^3}+6{{x}^2}+12x$.
Solución
En este caso, tenemos factores comunes tanto en la variable como en el coeficiente. En los coeficientes, el factor común es 3 y en las variables, el factor común es x:
$latex 3{{x}^3}+6{{x}^2}+12x=3x({{x}^2}+2x+4)$
EJERCICIO 7
Factoriza la expresión $latex 16{{x}^4}+32{{x}^3}-24{{x}^2}$.
Solución
El factor común de las variables es $latex {{x}^2}$ y el factor común de los coeficientes es 8. Entonces, tenemos:
$$16{{x}^4}+32{{x}^3}-24{{x}^2}=8{{x}^2}(2{{x}^2}+4x-3)$$
EJERCICIO 8
Factoriza la expresión $latex {{x}^2}{{y}^3}{{z}^4}+{{x}^4}y{{z}^3}$.
Solución
Aquí tenemos tres variables diferentes. El factor común contendrá la potencia más pequeña de cada variable. Entonces, el factor común es $latex {{x}^2}y{{z}^3}$. Escribimos la expresión extrayendo ese factor común:
$latex {{x}^2}{{y}^3}{{z}^4}+{{x}^4}y{{z}^3}={{x}^2}y{{z}^3}({{y}^2}z+{{x}^2})$
Ejercicios de factor común para resolver
Los siguientes ejercicios de factor común pueden ser usados para practicar este concepto. Factoriza las expresiones dadas y selecciona la respuesta correcta. Podrás verificar tu respuesta al hacer clic en “Verificar”.
Si tienes problemas con estos ejercicios, puedes estudiar los ejercicios resueltos de arriba.
Véase también
¿Interesado en aprender más sobre expresiones algebraicas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
