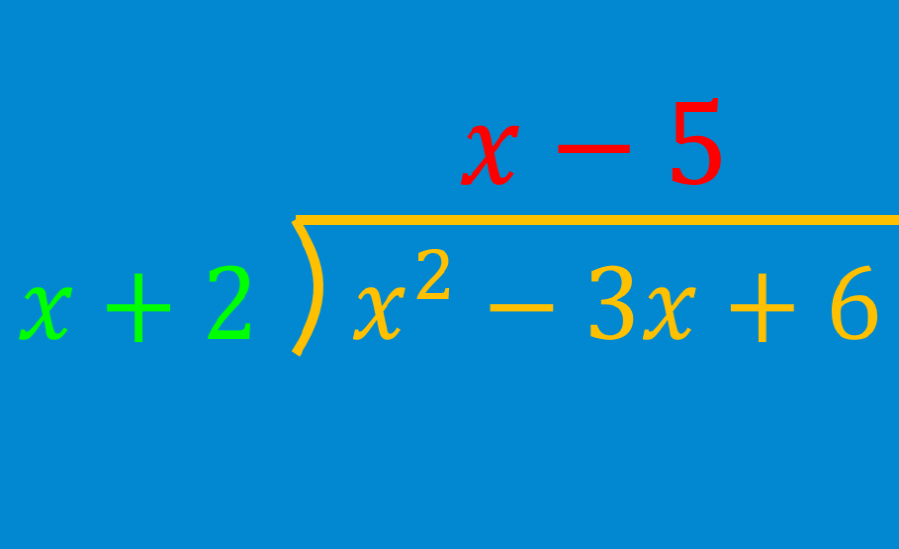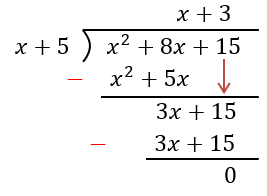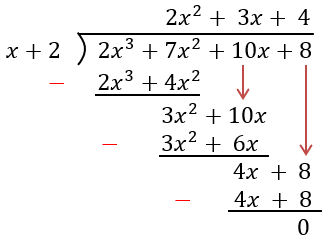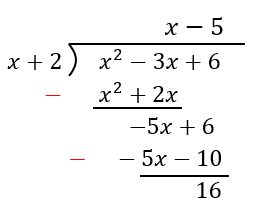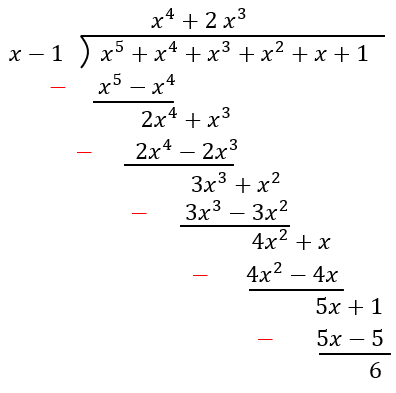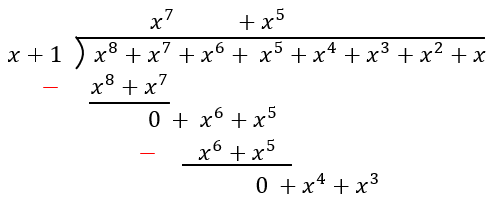Los polinomios pueden ser divididos usando la división larga de polinomios. Dividir a los polinomios en este formato nos permite visualizar de mejor manera cada uno de los pasos involucrados. Si es que obtenemos un residuo después de realizar la división, debemos incluirlo en la respuesta final al escribirlo como una fracción.
A continuación, veremos un resumen del proceso usado para dividir polinomios. También, veremos varios ejercicios de división de polinomios resueltos para visualizar la aplicación de este proceso.
Resumen de división de polinomios
Para dividir polinomios que contienen más de un término, tenemos que usar la llamada división larga de polinomios. Realizamos la división larga de polinomios siguiendo los siguientes pasos:
Paso 1: Tenemos que asegurarnos de que el polinomio está escrito en orden descendente. Si es que hay algún término faltante, usamos un cero para llenar un espacio o simplemente dejamos un espacio en blanco.
Paso 2: Dividimos al término con la potencia más grande dentro del símbolo de división por el término con la potencia más grande afuera del símbolo de división.
Paso 3: Multiplicamos o distribuimos la respuesta obtenida en el paso anterior por el polinomio en frente del símbolo de división.
Paso 4: Sustraemos lo obtenido y escribimos el siguiente término.
Paso 5: Repetimos los pasos 2, 3 y 4 hasta que ya no haya más términos restantes.
Paso 6: Escribimos la respuesta final. El término restante después de haber sustraído los últimos términos es el residuo. Debemos escribir al residuo como una fracción en la respuesta final.
Ejercicios de división de polinomios resueltos
El proceso de división larga mencionado arriba es usado para resolver los siguientes ejercicios de división de polinomios. Es recomendable que intentes resolver los ejercicios tú mismo antes de mirar la solución.
EJERCICIO 1
Resuelve la división de polinomios: $latex \frac{{{x}^2}+8x+15}{x+5}$.
Solución
Paso 1: Los polinomios ya están organizados en orden descendente.
Paso 2: Empezamos dividiendo al $latex {{x}^2}$ por x, lo cual es igual a x.
Paso 3: Al multiplicar esta respuesta por el polinomio en frente $latex (x+5)$, tenemos $latex {{x}^2}+5x$.
Paso 4: Restamos esta expresión y obtenemos $latex 3x$. Bajamos al 15 para completar al polinomio.
Paso 5: Al dividir $latex 3x$ por x, tenemos 3. Multiplicamos al 3 por $latex x+5$ para obtener $latex 3x+15$. Al restar obtenemos cero.
Paso 6: La respuesta final es $latex x+3$.
EJERCICIO 2
Resuelve la división de polinomios: $latex \frac{2{{x}^3}+7{{x}^2}+10x+8}{x+2}$.
Solución
Paso 1: Aquí también los polinomios están organizados descendentemente.
Paso 2: Empezamos dividiendo al $latex 2{{x}^3}$ por x, lo cual es igual a $latex 2{{x}^2}$.
Paso 3: Multiplicamos esto por el polinomio $latex x+2$, para obtener $latex 2{{x}^3}+4{{x}^2}$.
Paso 4: Restamos esta expresión para obtener $latex 3{{x}^2}$. Bajamos al 10x para completar al polinomio.
Paso 5: Al dividir $latex 3{{x}^2}$ por x, tenemos 3x. Multiplicando y restando, tenemos $latex 4x$. Bajamos el 8 para formar $latex 4x+8$. Al dividir $latex 4x$ por x, tenemos 4. Multiplicando y restando, tenemos 0.
Paso 6: La respuesta final es $latex 2{{x}^2}+3x+4$.
EJERCICIO 3
¿Cuál es el resultado de la división $latex \frac{{{x}^2}-3x+6}{x+2}$?
Solución
Paso 1: Los polinomios ya están organizados.
Paso 2: Empezamos dividiendo al $latex {{x}^2}$ por x, para obtener $latex x$.
Paso 3: Multiplicando por $latex x+2$, tenemos $latex {{x}^2}+4x$.
Paso 4: Restando, obtenemos $latex -5x$. Bajamos al 6 para completar al polinomio.
Paso 5: Al dividir $latex -5x$ por x, tenemos -5. Multiplicando y restando, tenemos 16.
Paso 6: La respuesta final es $latex x-5+\frac{16}{x+2}$.
EJERCICIO 4
¿Cuál es el resultado de la división $latex \frac{{{x}^5}+{{x}^2}+{{x}^4}+{{x}^3}+x+1}{x-1}$?
Solución
Paso 1: Empezamos organizando a los polinomios en orden descendente.
Paso 2: Dividimos al $latex {{x}^5}$ por x, para obtener $latex {{x}^4}$.
Paso 3: Multiplicando esto por $latex x-1$, tenemos $latex {{x}^5}-{{x}^4}$.
Paso 4: Restando esta expresión, tenemos $latex 2{{x}^4}$. Bajamos al $latex {{x}^3}$ para completar al polinomio.
Paso 5: Repetimos los pasos 2, 3, y 4 hasta completar la división y obtener 6 de residuo.
Paso 6: La respuesta final es $latex {{x}^4}+2{{x}^3}+\frac{6}{x-1}$.
EJERCICIO 5
Resuelve la división $latex \frac{{{x}^8}+{{x}^7}+{{x}^4}+{{x}^5}+{{x}^6}+{{x}^3}+{{x}^2}+x}{x+1}$.
Solución
Paso 1: Tenemos que ordenar a los polinomios descendentemente y dejamos espacio si es que no hay todos los términos.
Paso 2: Empezamos dividiendo al $latex {{x}^8}$ por x, para obtener $latex {{x}^7}$.
Paso 3: Multiplicamos esto por el polinomio $latex x+1$, para obtener $latex {{x}^8}+{{x}^7}$.
Paso 4: Restamos esta expresión para obtener 0. Bajamos los siguientes términos para dividir.
Paso 5: Al dividir $latex {{x}^6}$ por x, tenemos $latex {{x}^5}$. Multiplicando y restando, tenemos 0.
Paso 6: Podemos observar un patrón en la división. Los términos siempre se cancelan dejando un residuo de 0. Dado que tenemos un número par de términos en el divisor, el residuo será 0 y el cociente será $latex {{x}^7}+{{x}^5}+{{x}^3}+x$.
→ Calculadora de División de Polinomios
Ejercicios de división de polinomios para resolver
Practica la división de polinomios usando los siguientes ejercicios. Resuelve los ejercicios y selecciona la respuesta obtenida. Haz clic en “Verificar” para comprobar que obtuviste la respuesta correcta.
Véase también
¿Interesado en aprender más sobre operaciones con polinomios? Mira estas páginas: