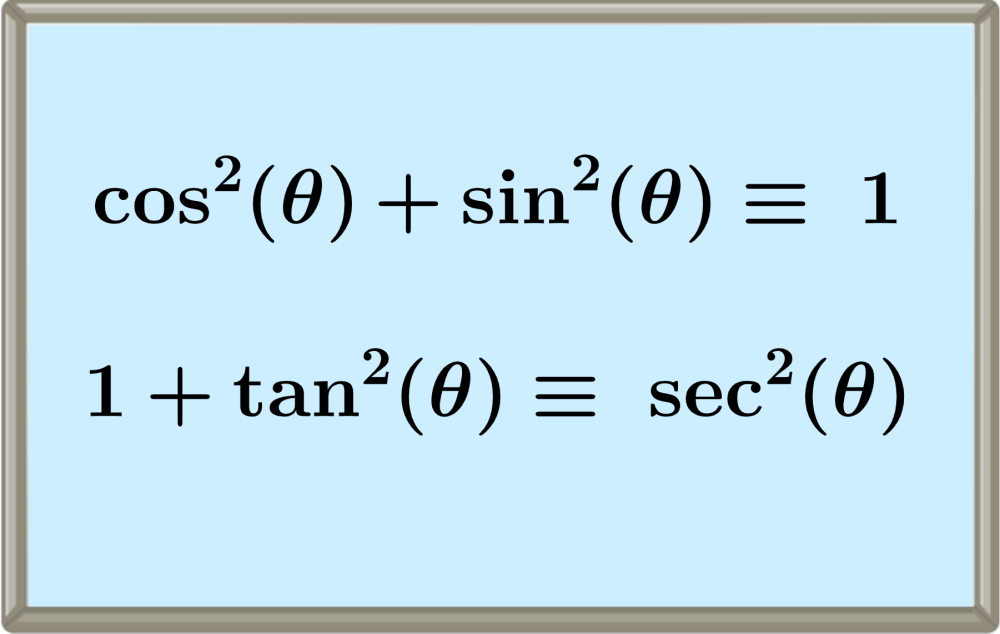Las identidades trigonométricas pueden ser demostradas al usar otras identidades trigonométricas más simples. Entonces, podemos usar las identidades simples para manipular las identidades trigonométricas originales hasta que ambos lados sean iguales o equivalentes a 0 o 1.
A continuación, aprenderemos el proceso general para demostrar identidades trigonométricas. Luego, aplicaremos lo aprendido para resolver algunos ejercicios de práctica.
¿Cómo demostrar identidades trigonométricas?
Para demostrar una identidad trigonométrica, tenemos que demostrar que la identidad es verdadera para todos los valores del ángulo.
Por ejemplo, consideremos a la siguiente identidad:
$$\tan(\theta)+\cot(\theta)\equiv \sec(\theta)\cosec(\theta)$$
Podríamos sustituir valores de θ en ambos lados de la identidad y esto demostraría que la identidad es verdadera para esos valores particulares de θ.
Sin embargo, esto no demuestra que la identidad es verdadera para todos los valores de θ.
Las identidades trigonométricas pueden ser demostradas al usar otras identidades más simples que sabemos que son verdaderas para todos los valores de θ.
Por ejemplo, sabemos que las siguientes identidades son verdaderas para todos los valores de θ:
- $latex \tan(\theta)\equiv \dfrac{\sin(\theta)}{\cos(\theta)}$
- $latex \sin^2(\theta)+\cos^2(\theta)\equiv 1$
- $latex 1+\tan^2(\theta)\equiv \sec^2(\theta)$
- $latex 1+\cot^2(\theta)\equiv \cosec^2(\theta)$
Entonces, podemos escoger el lado izquierdo (LI) o el lado derecho (LD) de la identidad y manipularlas usando las identidades simples hasta obtener la forma del otro lado.
Alternativamente, también es posible demostrar que la identidad es verdadera al mostrar que:
- $latex \text{LI} -\text{LD}\equiv 0~~$ o
- $latex \frac{\text{LI}}{\text{LD}}\equiv 1$
Ejercicios resueltos de demostrar identidades trigonométricas
EJERCICIO 1
Demuestra que la siguiente identidad es verdadera:
$$\tan (\theta)+\cot(\theta)\equiv \sec(\theta)\cosec(\theta)$$
Solución
Vamos a tomar el lado izquierdo y usaremos identidades simples hasta obtener la expresión del lado derecho:
$$\text{LI} \equiv \tan(\theta)+\cot(\theta)$$
$$ \equiv \frac{\sin(\theta)}{\cos(\theta)}+\frac{\cos(\theta)}{\sin(\theta)}$$
$$ \equiv \frac{\sin^2(\theta)+\cos^2(\theta)}{\sin(\theta) \cos(\theta)}$$
Ahora, podemos usar la identidad $latex \sin^2(\theta)+\cos^2(\theta)\equiv 1$:
$$\text{LI} \equiv \frac{1}{\sin(\theta) \cos(\theta)}$$
$$ \equiv \frac{1}{\sin(\theta) }\times \frac{1}{ \cos(\theta)}$$
$$ \equiv \cosec(\theta) \sec(\theta)\equiv LD$$
Entonces, hemos demostrado que la identidad es verdadera.
EJERCICIO 2
Demuestra la siguiente identidad trigonométrica:
$$\sin(\theta)\tan(\theta)+ \cos(\theta)\equiv \sec(\theta)$$
Solución
Vamos a manipular al lado izquierdo usando identidades trigonométricas simples:
$$\text{LI} \equiv \sin(\theta)\tan(\theta)+ \cos(\theta)$$
$$ \equiv \sin(\theta) \frac{\sin(\theta)}{\cos(\theta)}+\cos(\theta)$$
$$ \equiv \frac{\sin^2(\theta)}{\cos(\theta)}+ \cos(\theta)$$
Ahora, multiplicamos al numerador y al denominador de $latex \cos(\theta)$ por $latex \cos(\theta)$:
$$ \text{LI} \equiv \frac{\sin^2(\theta)}{\cos(\theta)}+ \frac{\cos^2(\theta)}{\cos(\theta)}$$
$$ \equiv \frac{\sin^2(\theta)+\cos^2(\theta)}{\cos(\theta)}$$
Usando la identidad $latex \sin^2(\theta)+\cos^2(\theta)\equiv 1$, tenemos:
$$\text{LI} \equiv \frac{1}{\cos(\theta)}$$
$$ \equiv \sec(\theta)\equiv LD$$
El lado izquierdo es igual al lado derecho. Entonces, la identidad es verdadera.
EJERCICIO 3
Demuestra la siguiente identidad trigonométrica:
$$\cosec(\theta)+\tan(\theta)\sec(\theta)\equiv \cosec(\theta) \sec^2(\theta)$$
Solución
Tomando el lado izquierdo, podemos manipular de la siguiente forma:
$$\text{LI} \equiv \cosec(\theta)+\tan(\theta)\sec(\theta)$$
$$ \equiv \frac{1}{\sin(\theta)}+\frac{\sin(\theta)}{\cos(\theta)} \times \frac{1}{\cos(\theta)}$$
$$ \equiv \frac{1}{\sin(\theta)}+\frac{\sin(\theta)}{\cos^2(\theta)}$$
$$ \equiv \frac{\cos^2(\theta)+\sin^2(\theta)}{\sin(\theta)\cos^2(\theta)}$$
Usando la identidad $latex \sin^2(\theta)+\cos^2(\theta)\equiv 1$, tenemos:
$$\text{LI} \equiv \frac{1}{\sin(\theta)\cos^2(\theta)}$$
$$ \equiv \frac{1}{\sin(\theta) }\times \frac{1}{ \cos^2(\theta)}$$
$$ \equiv \cosec(\theta) \sec^2(\theta)\equiv LD$$
Dado que ambos lados son iguales, la identidad es verdadera.
EJERCICIO 4
Usa identidades simples para demostrar la siguiente identidad trigonométrica:
$$(\sin(\theta)+\cos(\theta))^2-1\equiv 2 \sin(\theta)\cos(\theta)$$
Solución
Vamos a tomar el lado izquierdo de la identidad y vamos a expandir el binomio cuadrático:
$$\text{LI} \equiv (\sin(\theta)+\cos(\theta))^2-1$$
$$ \equiv \sin^2(\theta)+2\sin(\theta)\cos(\theta)+\cos^2(\theta)-1$$
$$ \equiv 2\sin(\theta)\cos(\theta)+(\sin^2(\theta)+\cos^2(\theta))-1$$
Usando la identidad $latex \sin^2(\theta)+\cos^2(\theta)\equiv 1$, tenemos:
$$\text{LI} \equiv 2\sin(\theta)\cos(\theta)+1-1$$
$$ \equiv 2\sin(\theta)\cos(\theta)$$
El lado izquierdo es igual al lado derecho, por lo que la identidad es verdadera.
EJERCICIO 5
Demuestra la siguiente identidad trigonométrica:
$$(\sin(\theta)-\cosec(\theta))^2\equiv \sin^2(\theta)+\cot^2(\theta)-1$$
Solución
Tomando el lado izquierdo y expandiendo el binomio cuadrado, tenemos:
$$\text{LI} \equiv (\sin(\theta)-\cosec(\theta))^2$$
$$ \equiv \sin^2(\theta)-2\sin(\theta)\cosec(\theta)+\cosec^2(\theta)$$
$$ \equiv \sin^2(\theta)-2\sin(\theta)\frac{1}{\sin(\theta)}+\cosec^2(\theta)$$
$$ \equiv \sin^2(\theta)-2+\cosec^2(\theta)$$
Ahora, podemos usar la identidad $latex \cosec^2(\theta)\equiv \cot^2(\theta)+ 1$:
$$\text{LI} \equiv \sin^2(\theta)-2+\cot^2(\theta)+ 1$$
$$ \equiv \sin^2(\theta)+\cot^2(\theta)- 1$$
Dado que el lado izquierdo pudo ser escrito como el lado derecho, la identidad es verdadera.
EJERCICIO 6
Usa identidades simples para demostrar la siguiente identidad trigonométrica:
$$ \frac{\cosec(\theta)}{\cot(\theta)+\tan(\theta)} \equiv \cos(\theta)$$
Solución
Vamos a manipular el lado izquierdo con identidades simples:
$$\text{LI} \equiv \frac{\cosec(\theta)}{\cot(\theta)+\tan(\theta)}$$
$$ \equiv \frac{\cosec(\theta)}{\frac{\cos(\theta)}{\sin(\theta)}+\frac{\sin(\theta)}{\cos(\theta)}}$$
$$ \equiv \frac{\cosec(\theta)}{\frac{\cos^2(\theta)+\sin^2(\theta)}{\sin(\theta)\cos(\theta)}}$$
Usando la identidad $latex \sin^2(\theta)+\cos^2(\theta)\equiv 1$, tenemos:
$$\text{LI} \frac{\cosec(\theta)}{\frac{1}{\sin(\theta)\cos(\theta)}}$$
$$ \equiv \cosec(\theta) \sin(\theta)\cos(\theta)$$
$$ \equiv \frac{1}{\sin(\theta)} \sin(\theta)\cos(\theta)$$
$$ \equiv \cos(\theta) \equiv LD$$
Entonces, hemos demostrado que la identidad es verdadera.
EJERCICIO 7
Demuestra la siguiente identidad trigonométrica:
$$ \frac{1}{1+\tan^2(\theta)}+\frac{1}{1+\cot^2(\theta)} \equiv 1$$
Solución
Tomando el lado izquierdo, tenemos:
$$\text{LI} \equiv \frac{1}{1+\tan^2(\theta)}+\frac{1}{1+\cot^2(\theta)}$$
Ahora, vamos a usar las identidades $latex 1+\tan^2(\theta)\equiv \sec^2(\theta)$ y $latex 1+\cot^2(\theta)\equiv \cosec^2(\theta)$:
$$\text{LI} \equiv \frac{1}{1+\sec^2(\theta)-1}+\frac{1}{1+\cosec^2(\theta)-1}$$
$$\equiv \frac{1}{\sec^2(\theta)}+\frac{1}{\cosec^2(\theta)}$$
$$\equiv \cos^2(\theta)+\sin^2(\theta)$$
Usando la identidad $latex \sin^2(\theta)+\cos^2(\theta)\equiv 1$, tenemos:
$$\text{LI} \equiv 1 \equiv LD$$
Dado que ambos lados son iguales, la identidad es verdadera.
EJERCICIO 8
Usa identidades simples para demostrar que la siguiente identidad es verdadera:
$$ (1-\sin(\theta)+\cos(\theta))^2\equiv 2(1-\sin(\theta))(1+\cos(\theta)) $$
Solución
Tomando el lado izquierdo, podemos expandir el binomio cuadrado:
$$\text{LI} \equiv (1-\sin(\theta)+\cos(\theta))^2$$
$$ \equiv (1-\sin(\theta)+\cos(\theta))(1-\sin(\theta)+\cos(\theta))$$
$$ \equiv 1-2\sin(\theta)+2\cos(\theta)+\sin^2(\theta)+\cos^2(\theta)-2\sin(\theta)\cos(\theta)$$
Usando la identidad $latex \sin^2(\theta)+\cos^2(\theta)\equiv 1$, tenemos:
$$ \text{LI} \equiv 2-2\sin(\theta)+2\cos(\theta)-2\sin(\theta)\cos(\theta)$$
$$ \equiv 2(1-\sin(\theta)+\cos(\theta)-\sin(\theta)\cos(\theta))$$
$$ \equiv 2(1-\sin(\theta))(1+\cos(\theta)) \equiv LD$$
Hemos demostrado la identidad.
EJERCICIO 9
Demuestra la siguiente identidad trigonométrica:
$$\frac{1+\sin(\theta)}{1-\sin(\theta)} \equiv (\tan(\theta)+\sec(\theta))^2$$
Solución
Tomando el lado derecho de la identidad, tenemos:
$$\text{LD} \equiv (\tan(\theta)+\sec(\theta))^2$$
$$ \equiv \left(\frac{\sin(\theta)}{\cos(\theta)}+\frac{1}{\cos(\theta)}\right)^2$$
$$ \equiv \left(\frac{\sin(\theta)+1}{\cos(\theta)}\right)^2$$
$$ \equiv \frac{(1+\sin(\theta))^2}{\cos^2(\theta)}$$
Ahora, podemos usar la identidad $latex \sin^2(\theta)+\cos^2(\theta)\equiv 1$:
$$\text{LD} \equiv \frac{(1+\sin(\theta))^2}{1-\sin^2(\theta)}$$
$$ \equiv \frac{(1+\sin(\theta))^2}{(1+\sin(\theta))(1-\sin(\theta))}$$
$$ \equiv \frac{1+\sin(\theta)}{1-\sin(\theta)}\equiv LI$$
Como ambos lados son iguales, la identidad es verdadera.
EJERCICIO 10
Demuestra que la siguiente identidad es verdadera:
$$ \sqrt{\sec^2(\theta)-1}+\sqrt{\cosec^2(\theta)-1}\equiv \frac{1}{\sin(\theta)\cos(\theta)}$$
Solución
Podemos simplificar el lado izquierdo usando las identidades $latex 1+\tan^2(\theta)\equiv \sec^2(\theta)$ y $latex 1+\cot^2(\theta)\equiv \cosec^2(\theta)$:
$$\text{LI} \equiv \sqrt{\sec^2(\theta)-1}+\sqrt{\cosec^2(\theta)-1}$$
$$ \equiv \sqrt{\tan^2(\theta)+1-1}+\sqrt{\cot^2(\theta)+1-1}$$
$$ \equiv \sqrt{\tan^2(\theta)}+\sqrt{\cot^2(\theta)}$$
$$ \equiv \tan(\theta)+ \cot(\theta)$$
$$ \equiv \frac{\sin(\theta)}{\cos(\theta)}+ \frac{\cos(\theta)}{\sin(\theta)}$$
$$ \equiv \frac{\sin^2(\theta)+\cos^2(\theta)}{\cos(\theta)\sin(\theta)}$$
Usando la identidad $latex \sin^2(\theta)+\cos^2(\theta)\equiv 1$, tenemos:
$$\text{LI} \equiv \frac{1}{\sin(\theta) \cos(\theta)} \equiv LD$$
Entonces, hemos demostrado que la identidad es verdadera.
Véase también
¿Interesado en aprender más sobre identidades trigonométricas? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
