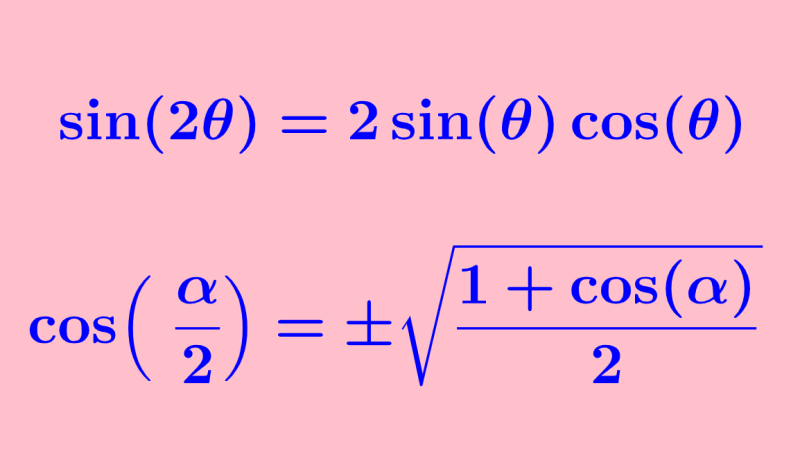Las identidades trigonométricas son útiles cuando queremos reescribir o simplificar expresiones trigonométricas. Las identidades trigonométricas son verdaderas para cada valor que ocurre en ambos lados de una ecuación. Todas las identidades trigonométricas son derivadas de las seis funciones trigonométricas fundamentales, las cuales son seno, coseno, tangente, cosecante, secante y cotangente. Por su parte, estas funciones trigonométricas son definidas usando los lados del triángulo rectángulo, es decir, el lado opuesto, el lado adyacente y la hipotenusa.
A continuación conoceremos las fórmulas de las identidades trigonométricas más comunes.
- Fórmulas de las identidades recíprocas
- Fórmulas de las identidades Pitagóricas
- Fórmulas de las identidades del cociente
- Fórmulas de las identidades de ángulos negativos
- Fórmulas de las identidades de ángulos complementarios
- Fórmulas de las identidades de suma y resta de ángulos
- Fórmulas de las identidades de ángulos dobles
- Fórmulas de las identidades de ángulos medios
- Véase también
Fórmulas de las identidades recíprocas
Un recíproco de una fracción es definido como una fracción que tiene al numerador y al denominador cambiados de posiciones. Las identidades recíprocas son definidas con respecto a las funciones trigonométricas fundamentales, seno, coseno y tangente.
Cada función trigonométrica fundamental produce una identidad recíproca. Por ejemplo, la función seno es definida como el lado opuesto dividido por la hipotenusa, es decir, $latex \sin(\theta)=\frac{O}{H}$.
La función cosecante es la recíproca del seno, por lo que tenemos $latex \csc(\theta)=\frac{H}{O}$. Si es que tenemos $latex \sin(\theta)=\frac{1}{2}$, entonces, también tenemos $latex \csc(\theta)=2$.
De igual forma, la función secante es la función recíproca del coseno y la función cotangente es la función recíproca de la tangente. Entonces, tenemos las fórmulas:
| $latex \csc(\theta)=\frac{1}{\sin(\theta)}$ $latex \sec(\theta)=\frac{1}{\cos(\theta)}$ $latex \cot(\theta)=\frac{1}{\tan(\theta)}$ |
Fórmulas de las identidades Pitagóricas
Las identidades Pitagóricas son derivadas del teorema de Pitágoras. En un círculo unitario, las coordenadas x corresponden a coseno y las coordenadas y corresponden a seno. Además, el radio unitario corresponde a la hipotenusa, por lo que tenemos:
| $latex {{\sin}^2} (\theta)+{{\cos}^2} (\theta)=1$ |
Esta es la identidad Pitagórica principal. A partir de esta identidad, podemos dividirla por seno o coseno para obtener las siguientes variaciones:
| $latex {{\tan}^2} (\theta)+1={{\sec}^2} (\theta)$ $latex 1+{{\cot}^2} (\theta)={{\csc}^2} (\theta)$ |
En estas identidades, «tan» representa a la tangente, «sec» representa a la secante, «cot» representa a la cotangente y «csc» representa a la cosecante.
Fórmulas de las identidades del cociente
Las identidades de cociente son fórmulas que relacionan a la tangente y a la cotangente en términos del seno y del coseno. La función seno es definida como el lado opuesto dividido por la hipotenusa y la función coseno es definida como el lado adyacente dividido por la hipotenusa.
Estas definiciones pueden ser usadas para comprobar las siguientes fórmulas de las identidades del cociente:
| $latex \tan(\theta)=\frac{\sin(\theta)}{\cos(\theta)}$ $latex \cot(\theta)=\frac{\cos(\theta)}{\sin(\theta)}$ |
Fórmulas de las identidades de ángulos negativos
Las identidades de ángulos negativos relacionan a las funciones trigonométricas de un ángulo negativo con expresiones trigonométricas de un ángulo positivo. Estas identidades usan las definiciones de las funciones par e impar. Entonces, tenemos:
| $latex \sin(-\theta)=-\sin(\theta)$ $latex \cos(-\theta)=\sin(\theta)$ $latex \tan(-\theta)=-\tan(\theta)$ $latex \cot(-\theta)=-\cot(\theta)$ $latex \sec(-\theta)=\sec(\theta)$ $latex \csc(-\theta)=-\csc(\theta)$ |
Fórmulas de las identidades de ángulos complementarios
Las identidades de ángulos complementarios relacionan a dos funciones trigonométricas a través de ángulos complementarios. Dos ángulos son complementarios cuando suman 90°.
Entonces, para encontrar un ángulo complementario, restamos al ángulo original de 90°. Las fórmulas de estas identidades son:
| $latex \sin(90^{\circ} -\theta)=\cos(\theta)$ $latex \cos(90^{\circ} -\theta)=\sin(\theta)$ $latex \tan(90^{\circ} -\theta)=\cot(\theta)$ $latex \cot(90^{\circ} -\theta)=\tan(\theta)$ $latex \sec(90^{\circ} -\theta)=\csc(\theta)$ $latex \csc(90^{\circ} -\theta)=\sec(\theta)$ |
Fórmulas de las identidades de suma y resta de ángulos
Las identidades de suma y resta de ángulos son usadas principalmente para encontrar los valores exactos de un ángulo, el cual puede ser escrito como una suma o resta de ángulos comunes como 30°, 45°, 60°, 90° y sus múltiplos. Esto se debe a que generalmente, los valores de estos ángulos son conocidos.
Las fórmulas de las identidades de la suma de ángulos son:
| $latex \sin(A+B)=\sin(A)\cos(B)+\cos(A)\sin(B)$ $latex \cos(A+B)=\cos(A)\cos(B)-\sin(A)\sin(B)$ $latex \tan(A+B)=\frac{\tan(A)+\tan(B)}{1-\tan(A)\tan(B)}$ |
Las fórmulas de las identidades de la resta de ángulos son:
| $latex \sin(A-B)=\sin(A)\cos(B)-\cos(A)\sin(B)$ $latex \cos(A-B)=\cos(A)\cos(B)+\sin(A)\sin(B)$ $latex \tan(A-B)=\frac{\tan(A)-\tan(B)}{1+\tan(A)\tan(B)}$ |
Fórmulas de las identidades de ángulos dobles
Las identidades de ángulos dobles son derivadas a partir de las identidades de suma de ángulos. Estas identidades son usadas cuando conocemos el valor de θ y tenemos que encontrar el valor de seno, coseno o tangente de 2θ.
La fórmula de la identidad de ángulo doble para el seno es:
| $latex \sin(2x)=2\sin(x)\cos(x)$ |
La identidad de ángulo doble para el coseno tiene tres variaciones, dos de las cuales son obtenidas al usar la identidad Pitagórica:
| $latex \cos(2x)={{\cos}^2}(x)-{{\sin}^2}(x)$ $latex =2{{\cos}^2}(x)-1$ $latex =1-2{{\sin}^2}(x)$ |
La fórmula de la identidad de ángulo doble para la tangente es:
| $latex \tan(2x)=\frac{2\tan(x)}{1-{{\tan}^2}(x)}$ |
Fórmulas de las identidades de ángulos medios
Las identidades de ángulos medios son derivadas usando las identidades de ángulo doble y sustituyendo por $latex \frac{\theta}{2}$. Estas identidades trigonométricas son usadas cuando conocemos el valor de seno, coseno o tangente de θ y queremos encontrar el valor de $latex \frac{\theta}{2}$.
Estas identidades también nos pueden ayudar a transformar expresiones trigonométricas que tienen exponentes a una sin exponentes.
La fórmula de la identidad de ángulo medio del seno es:
| $latex \sin(\frac{\theta}{2})=\pm \sqrt{\frac{1-\cos(\theta)}{2}}$ |
La fórmula de la identidad de ángulo medio del coseno es:
| $latex \cos(\frac{\theta}{2})=\pm \sqrt{\frac{1+\cos(\theta)}{2}}$ |
La fórmula de la identidad de ángulo medio de la tangente es:
| $latex \tan(\frac{\theta}{2})=\frac{\sin(\theta)}{1+\cos(\theta)}$ $latex =\frac{1-\cos(\theta)}{\sin(\theta)}$ |
Véase también
¿Interesado en aprender más sobre identidades trigonométricas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
