Las identidades trigonométricas son ecuaciones, las cuales son verdaderas para cualquier ángulo usado. Las identidades trigonométricas son usadas para reescribir a expresiones trigonométricas y simplificarlas o resolverlas. Estas identidades son derivadas a partir de las funciones trigonométricas fundamentales, seno, coseno y tangente. Además, el círculo unitario y el teorema de Pitágoras son usados para obtener más identidades.
A continuación, conoceremos las fórmulas de las identidades trigonométricas fundamentales. Luego, usaremos estas identidades para resolver algunos ejercicios de práctica.
TRIGONOMETRÍA
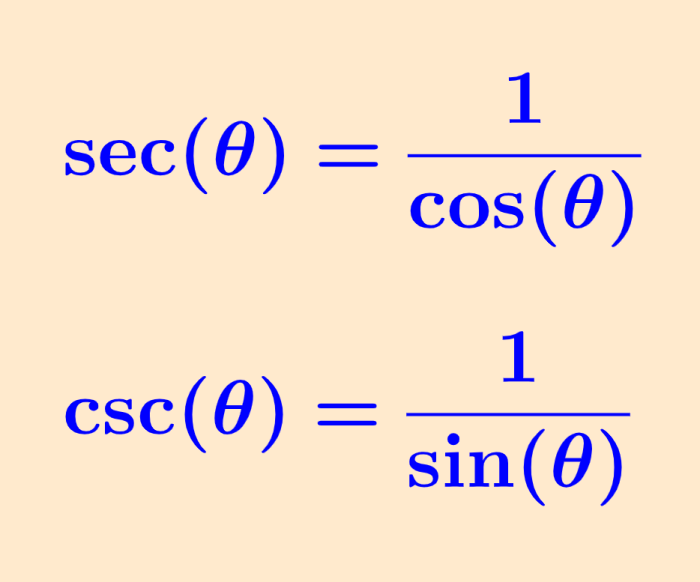
Relevante para…
Aprender sobre las identidades trigonométricas fundamentales.
TRIGONOMETRÍA
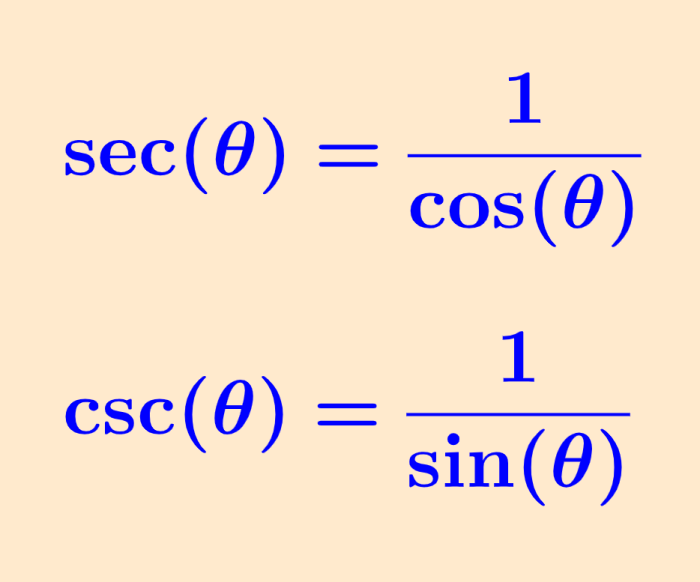
Relevante para…
Aprender sobre las identidades trigonométricas fundamentales.
¿Cuáles son las identidades trigonométricas fundamentales?
Existen varias identidades trigonométricas que pueden ser derivadas a partir de las definiciones de las funciones trigonométricas. Además, el círculo unitario y el teorema de Pitágoras son usados para obtener más identidades.
Finalmente, las mismas identidades trigonométricas son usadas para derivar y obtener variaciones de identidades trigonométricas que pueden ser aplicadas en otras situaciones.
Esto significa que existen varias fórmulas de las identidades trigonométricas, sin embargo, las más importantes son las identidades recíprocas, las identidades del cociente, las identidades de ángulos complementarios, las identidades de ángulos negativos y las identidades Pitagóricas.
Identidades recíprocas
Estas identidades son definidas a partir de las funciones trigonométricas seno, coseno y tangente. Un recíproco de una fracción es igual al numerador y al denominador intercambiados de posición. Podemos formar un recíproco al escribir uno sobre la cantidad original. Entonces, definimos a las funciones cosecante, secante y contangente:
$latex \csc(\theta)=\frac{1}{\sin(\theta)}$
$latex \sec(\theta)=\frac{1}{\cos(\theta)}$
$latex \cot(\theta)=\frac{1}{\tan(\theta)}$
Identidades del cociente
Estas identidades son encontradas al escribir a la tangente y a la cotangente en términos del seno y del coseno. Entonces, tenemos:
$latex \tan(\theta)=\frac{\sin(\theta)}{\cos(\theta)}$
$latex \cot(\theta)=\frac{\cos(\theta)}{\sin(\theta)}$
Identidades de ángulos complementarios
Los ángulos complementarios son ángulos que suman 90°. Podemos usar a estos ángulos para definir identidades trigonométricas que relacionan a las funciones trigonométricas:
$latex \sin(\theta)=\cos(90^{\circ} -\theta)$
$latex \cos(\theta)=\sin(90^{\circ} -\theta)$
$latex \tan(\theta)=\cot(90^{\circ} -\theta)$
$latex \cot(\theta)=\tan(90^{\circ} -\theta)$
Identidades de ángulos negativos
Usando las definiciones de funciones pares e impares, podemos encontrar identidades para ángulos negativos y escribirlos como ángulos positivos.
$latex \sin(-\theta)=-\sin(\theta)$
$latex \cos(-\theta)=\cos(\theta)$
$latex \tan(-\theta)=-\tan(\theta)$
Identidades Pitagóricas
La primera identidad Pitagórica es derivada usando el teorema de Pitágoras en un círculo unitario. Las otras dos variaciones son encontradas al dividir a la identidad Pitagórica principal por seno o coseno y simplificar.
$latex {{\sin}^2}(\theta)+{{\cos}^2}(\theta)=1$
$latex {{\tan}^2}(\theta)+1={{\sec}^2}(\theta)$
$latex {{\cot}^2}(\theta)+1={{\csc}^2}(\theta)$
Ejercicios de identidades trigonométricas fundamentales resueltos
Los siguientes ejercicios son resueltos aplicando las identidades trigonométricas fundamentales vistas arriba. Cada ejercicio tiene su respectiva solución, en donde puedes observar el proceso usado.
EJERCICIO 1
Usa las identidades Pitagóricas para simplificar la expresión trigonométrica $latex \sin(x){{\cos}^2}(x)-\sin(x)$.
Solución
Observamos que la expresión tiene al seno y al coseno. Esto significa que podemos usar la identidad $latex {{\sin}^2}(x)+{{\cos}^2}(x)=1$. Sin embargo, tenemos que empezar factorizando a la expresión dada:
$$\sin(x){{\cos}^2}(x)-\sin(x)=\sin(x)({{\cos}^2}(x)-1)$$
Además, vamos a reescribir a la identidad $latex {{\sin}^2}(x)+{{\cos}^2}(x)=1$ de la siguiente forma: $latex {{\cos}^2}(x)-1=-{{\sin}^2}(x)$ y la reemplazamos en la identidad para obtener:
$$\sin(x)({{\cos}^2}(x)-1)=\sin(x)(-{{\sin}^2}(x))$$
$latex ={{\sin}^3}(x)$
EJERCICIO 2
Calcula el valor de $latex \tan(\theta)$ usando los valores $latex \cos(\theta)=\frac{3}{11}$ y $latex \sin(\theta)=\frac{5}{11}$.
Solución
En este caso, podemos usar a la identidad del cociente de la tangente y escribirla en términos de seno y coseno. Entonces, el valor de la tangente es:
$latex \tan(\theta)=\frac{\sin(\theta)}{\cos(\theta)}$
$latex \tan(\theta)=\frac{\frac{5}{11}}{\frac{3}{11}}$
$latex \tan(\theta)=\frac{5}{3}$
EJERCICIO 3
Determina el valor de $latex \tan(\theta)$ usando $latex \cot(\theta)=\frac{5}{3}$.
Solución
Podemos resolver este ejercicio usando la identidad recíproca de la tangente. La cotangente es la función recíproca de la tangente, por lo que encontramos el valor de la tangente al «darle la vuelta» al valor de la cotangente. Entonces, tenemos:
$latex \cot(\theta)=\frac{5}{3}$
⇒ $latex \tan(\theta)=\frac{3}{5}$
EJERCICIO 4
Usa las identidades trigonométricas para simplificar la expresión: $$({{\sec}^2}(x))(1-{{\sin}^2}(x))-(\frac{\sin(x)}{\csc(x)}+\frac{\cos(x)}{\sec(x)})$$.
Solución
Podemos empezar usando las identidades recíprocas $latex \sec(x)=\frac{1}{\cos(x)}$ y $latex \csc(x)=\frac{1}{\sin(x)}$. Entonces, tenemos:
$$({{\sec}^2}(x))(1-{{\sin}^2}(x))-(\frac{\sin(x)}{\csc(x)}+\frac{\cos(x)}{\sec(x)})$$
$$=({{\sec}^2}(x))(1-{{\sin}^2}(x))-({{\sin}^2}(x)+{{\cos}^2}(x))$$
Ahora, vamos a usar la identidad Pitagórica principal para resolver completamente:
$latex =({{\sec}^2}(x))({{\cos}^2}(x))-(1)$
$latex =1-1$
$latex =0$
Ejercicios de identidades trigonométricas fundamentales para resolver
Usa las fórmulas de las identidades trigonométricas fundamentales vistas arriba para resolver los siguientes ejercicios. Selecciona una respuesta y haz clic en «Verificar» para comprobar que obtuviste la respuesta correcta.
Véase también
¿Interesado en aprender más sobre identidades trigonométricas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
