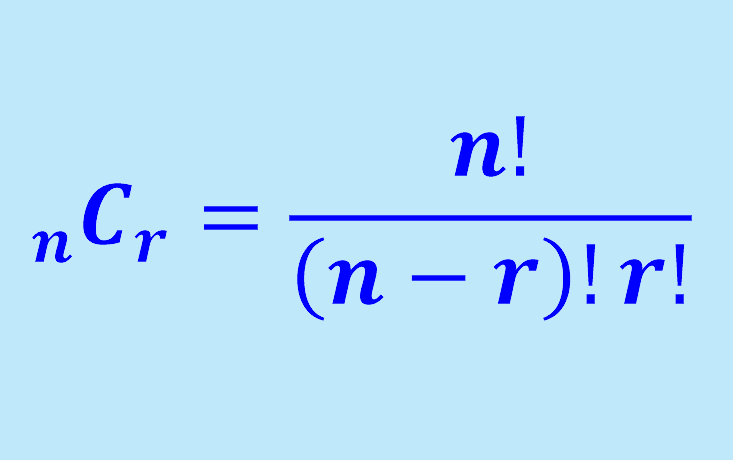Las combinaciones son usadas para contar el número de maneras diferentes en las que ciertos grupos pueden ser escogidos de un conjunto si es que el orden de los objetos no importa. Esto es diferente a las permutaciones, en donde el orden de los objetos sí importa.
A continuación, miraremos un resumen breve de las combinaciones junto con su fórmula y la terminología usada. Además, veremos ejercicios resueltos para aprender sobre la aplicación de la fórmula de combinaciones.
Resumen de combinaciones
Las combinaciones son selecciones de objetos de una colección, de tal forma que el orden de la selección no importa. En las combinaciones, podemos seleccionar los objetos en cualquier orden. Por ejemplo, si es que tenemos ab y ba, estas selecciones son consideradas iguales en las combinaciones.
La fórmula para determinar el número de organizaciones posibles al seleccionar unos pocos objetos de un conjunto sin repeticiones es expresada en la siguiente manera:
| $latex _{n}{{C}_{k}}=\frac{{n!}}{{\left( {n-k} \right)!k!}}$ |
en donde:
- n es el número total de elementos en un conjunto
- k es el número de objetos seleccionados
- ! es el símbolo de factorial
Recordemos que el factorial (denotado como “!“) es un producto de todos los números enteros positivos menores o igual al número que precede al factorial. Por ejemplo, $latex 3!=1 \times 2 \times 3=6$.
Ejercicios de combinaciones resueltos
Con los siguientes ejercicios, puedes practicar la aplicación de la fórmula de combinaciones. Cada ejercicio tiene su respectiva solución para analizar cuál es el razonamiento detrás de cada respuesta.
EJERCICIO 1
Encuentra el resultado de la combinación $latex _{8}C_{6}$.
Solución
Usamos la fórmula de combinaciones $latex _{n}{{C}_{k}}=\frac{{n!}}{{\left( {n-k} \right)!k!}}$ y reemplazamos $latex n=8$ y $latex k=6$:
$latex _{8}{{C}_{6}}=\frac{{8!}}{{\left( {8-6} \right)!6!}}$
$latex =\frac{{8!}}{{\left( {2} \right)!6!}}$
Ahora, reconocemos que podemos escribir a 8! como $latex 8\times 7\times 6!$ y eliminamos a 6! tanto en el numerador como en el denominador:
$latex \frac{{8!}}{{\left( {2} \right)!6!}}=\frac{{8\times 7}}{2}$
$latex =4\times 7=28$
EJERCICIO 2
Encuentra el resultado de la combinación $latex _{9}C_{4}$.
Solución
Reemplazamos $latex n=9$ y $latex k=4$ en la fórmula $latex _{n}{{C}_{k}}=\frac{{n!}}{{\left( {n-k} \right)!k!}}$:
$latex _{9}{{C}_{4}}=\frac{{9!}}{{\left( {9-4} \right)!4!}}$
$latex =\frac{{9!}}{{\left( {5} \right)!4!}}$
Ahora, reconocemos que podemos escribir a 9! como $latex 9\times 8\times 7\times 6\times 5!$ y eliminamos a 5! tanto en el numerador como en el denominador:
$latex \frac{{9!}}{{\left( {5} \right)!4!}}=\frac{{9\times 8\times 7\times 6}}{4!}$
Reescribimos a 4! como $latex 4\times 3\times 2\times 1$ y simplificamos:
$latex \frac{{9\times 8\times 7\times 6}}{4\times 3\times 2\times 1}=126$
EJERCICIO 3
Encuentra la combinación $latex _{100}C_{100}$.
Solución
Reemplazamos $latex n=100$ y $latex k=100$ en la fórmula $latex _{n}{{C}_{k}}=\frac{{n!}}{{\left( {n-k} \right)!k!}}$:
$latex _{100}{{C}_{100}}=\frac{{100!}}{{\left( {100-100} \right)!100!}}$
$latex =\frac{{100!}}{{\left( {1} \right)!100!}}$
Fácilmente podemos eliminar a 100! tanto del denominador como del numerador:
$latex \frac{{100!}}{{\left( {1} \right)!100!}}=1$
Este resultado tiene sentido, ya que solo hay una manera posible de seleccionar a 100 objetos de un conjunto de 100 objetos si es el orden no importa.
EJERCICIO 4
¿Cuántas maneras existen de escoger a un equipo de 3 personas de un grupo de 10?
Solución
En este caso, escogemos a 3 personas por lo que tenemos $latex k=3$. El grupo total es $latex n=10$. Usando estos datos en la fórmula $latex _{n}{{C}_{k}}=\frac{{n!}}{{\left( {n-k} \right)!k!}}$, tenemos:
$latex _{10}{{C}_{3}}=\frac{{10!}}{{\left( {10-3} \right)!3!}}$
$latex =\frac{{10!}}{{\left( {7} \right)!3!}}$
Podemos expandir el 10! hasta obtener 7! y simplificamos esto:
$latex \frac{10!}{(3)!3!}=\frac{10\times 9 \times 8 \times 7!}{(7)!3!}$
$latex =\frac{{10\times 9 \times 8}}{{3!}}$
$latex =\frac{{10\times 9 \times 8}}{{6}}$
$latex =120$
EJERCICIO 5
Supón que tenemos que seleccionar a 5 nuevos empleados de una lista de 10 aplicantes. ¿En cuántas maneras puede ser esto realizado?
Solución
En este caso, tenemos $latex n=10$ y $latex k=5$, entonces tenemos:
$latex _{10}{{C}_{5}}=\frac{{10!}}{{\left( {10-5} \right)!5!}}$
$latex =\frac{{10!}}{{\left( {5} \right)!5!}}$
Podemos reescribir a 10! hasta obtener 5! y simplificamos:
$latex \frac{{10!}}{{\left( {5} \right)!5!}}=\frac{{10 \times 9\times 8 \times 7 \times 6 \times 5!}}{{\left( {5} \right)!5!}}$
$latex =\frac{{10 \times 9\times 8 \times 7 \times 6}}{{5!}}$
$latex =\frac{10 \times 9\times 8 \times 7 \times 6}{5 \times 4\times 3 \times 2 \times 1}$
$latex =252$
EJERCICIO 6
En un concesionario de autos hay 3 autos de un modelo particular que deben ser transportados a otro concesionario. Si es que hay un total de 25 autos de este modelo, ¿cuántas opciones disponibles hay para transportar?
Solución
Reconocemos que tenemos $latex n=25$ y $latex k=3$ y reemplazamos estos valores en la fórmula $latex _{n}{{C}_{k}}=\frac{{n!}}{{\left( {n-k} \right)!k!}}$:
$latex _{25}{{C}_{3}}=\frac{{25!}}{{\left( {25-3} \right)!3!}}$
$latex =\frac{{25!}}{{\left( {22} \right)!3!}}$
Reescribimos al factorial 25! hasta que lleguemos a 22!:
$latex \frac{{25!}}{{\left( {22} \right)!3!}}=\frac{{25 \times 24 \times 23 \times 22!}}{{\left( {22} \right)!3!}}$
Ahora, simplificamos a 22! en el numerador y el denominador:
$latex \frac{{25 \times 24 \times 23 \times 22!}}{{\left( {22} \right)!3!}}=\frac{{25 \times 24 \times 23}}{{3!}}$
$latex =25 \times 4 \times 23=2300$
EJERCICIO 7
Supón que tenemos una oficina de 5 mujeres y 6 hombres y tenemos que seleccionar un comité de 4 personas. ¿En cuántas maneras podemos seleccionar a 2 hombres y 2 mujeres?
Solución
En este caso, tenemos que encontrar dos combinaciones diferentes y luego multiplicarlas. Entonces, queremos calcular $latex (_{5}{{C}_{2}})(_{6}{{C}_{2}})$. Podemos calcular estas combinaciones separadamente:
$latex _{5}{{C}_{2}}=\frac{{5!}}{{\left( {5-2} \right)!2!}}$
$latex =\frac{{5!}}{{\left( {3} \right)!2!}}$
$latex =\frac{{5\times 4\times 3!}}{{\left( {3} \right)!2!}}$
$latex =\frac{{5\times 4}}{{2!}}=10$
$latex _{6}{{C}_{2}}=\frac{{6!}}{{\left( {6-2} \right)!2!}}$
$latex =\frac{{6!}}{{\left( {4} \right)!2!}}$
$latex =\frac{{6\times 5\times 4!}}{{\left( {4} \right)!2!}}$
$latex =\frac{{6\times 5}}{{2!}}=15$
Entonces, tenemos $latex (_{5}{{C}_{2}})(_{6}{{C}_{2}})=10\times 15=150$.
→ Calculadora de Combinaciones (nCr)
Ejercicios de combinaciones para resolver
Pon en práctica tu conocimiento sobre combinaciones con los siguientes ejercicios. Resuelve las combinaciones y selecciona una respuesta. Verifícala para asegurarte que seleccionaste la correcta.
Véase también
¿Interesado en aprender más sobre combinaciones y permutaciones? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
