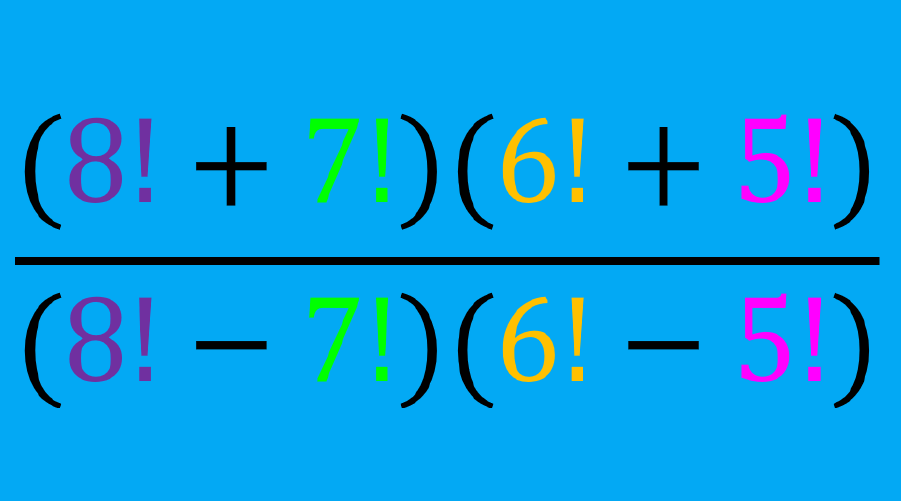Los factoriales son simplemente productos, indicados por un signo de exclamación. Los factoriales indican que hay una multiplicación de todos los números desde el 1 hasta ese número. Expresiones algebraicas con factoriales pueden ser simplificadas al expandir los factoriales y buscar factores comunes.
A continuación, miraremos un resumen de los factoriales. También, veremos varios ejercicios de factoriales y simplificación de factoriales resueltos para entender el razonamiento usado a la hora de resolver este tipo de ejercicios.
ÁLGEBRA
Relevante para…
Resolver ejercicios de factoriales y simplificación de factoriales.
ÁLGEBRA
Relevante para…
Resolver ejercicios de factoriales y simplificación de factoriales.
Resumen de factoriales
Representamos a los factoriales con el signo de exclamación “!” colocado luego del número o variable. El signo de exclamación significa que tenemos que multiplicar todos los números enteros que se encuentran entre el número y 1.
Por ejemplo:
| $latex 5!=1\times 2 \times 3 \times 4 \times 5=120$ |
Generalmente, leímos esto como “5 factorial”, aunque también podemos leerlo como “factorial de 5”.
Por varias razones, 0! es definido como ser igual a 1, no a 0, por lo que es recomendable memorizarse esto.
Simplificación de factoriales
Cuando tenemos factoriales tanto en el numerador como en el denominador, podemos fácilmente simplificar esto al expandir los factoriales y simplificar los números correspondientes.
Para simplificar expresiones factoriales con variables tanto en el numerador como en el denominador, queremos formar factores comunes de modo que podamos cancelar. Lo fundamental es comparar los factoriales y determinar cuál tiene un valor más grande.
Por ejemplo, si tenemos los factoriales $latex (n+3)!$ y $latex (n+1)!$, fácilmente sabemos que $latex (n+3)!$ es mayor, por lo que lo expandimos hasta que $latex (n+1)!$ aparezca en la sucesión para luego simplificar:
$latex (n+3)!=(n+3)(n+2)(n+1)!$
Ejercicios de factoriales resueltos
Los siguientes ejercicios indican la simplificación de factoriales. Cada ejercicio tiene su respectiva solución, la cual detalla el razonamiento usado para resolver el problema. Intenta resolver los ejercicios tú mismo antes de mirar la solución.
EJERCICIO 1
Encuentra el resultado del factorial 8!.
Solución
Podemos evaluar esto al expandir totalmente el factorial:
$latex 8!=1 \times 2 \times 3 \times 4 \times 5 \times 6 \times 7 \times 8$
$latex =40 320$
Podemos ver que obtuvimos un número grande. Los factoriales crecen rápidamente.
EJERCICIO 2
Simplifica la expresión factorial $latex \frac{6!}{4!}$.
Solución
Tenemos que expandir los factoriales para simplificar:
$latex \frac{6!}{4!}=\frac{1 \times 2\times 3\times 4 \times 5\times 6}{1 \times 2\times 3\times 4}$
Vemos que los números desde el 1 al 4 se repiten tanto en el numerador como en el denominar, por lo que podemos eliminarlos:
$latex \frac{1 \times 2\times 3\times 4 \times 5\times 6}{1 \times 2\times 3\times 4}= 5\times 6$
$latex =30$
EJERCICIO 3
Simplifica la expresión factorial $latex \frac{5!}{2!3!}$.
Solución
Expandiendo estos factoriales, tenemos:
$latex \frac{5!}{2!3!}=\frac{5\times 4\times 3\times 2\times 1}{(2\times 1)(3\times 2\times 1)}$
Podemos simplificar los números del 1 al 3. También podemos simplificar al 4 con el 2:
$latex \frac{5\times 4\times 3\times 2\times 1}{(2\times 1)(3\times 2\times 1)}=10$
EJERCICIO 4
Simplifica lo siguiente: $latex \frac{17!}{14!3!}$.
Solución
Empezamos expandiendo los factoriales:
$latex \frac{17!}{14!3!}=\frac{1\times 2\times 3\times 4…14\times 15 \times 16 \times 17}{(1\times 2\times 3\times 4 …14)(1\times 2 \times 3)}$
Ahora, podemos simplificar los números del 1 al 14 que son comunes tanto para 14! como para 17!:
$latex \frac{1\times 2\times 3\times 4…14\times 15 \times 16 \times 17}{(1\times 2\times 3\times 4 …14)(1\times 2 \times 3)}=\frac{ 15 \times 16 \times 17}{1\times 2 \times 3}$
Ahora, podemos simplificar al 2 y al 3 con el 16 y el 15:
$latex \frac{ 15 \times 16 \times 17}{1\times 2 \times 3}=5\times 8 \times 17=680$
En este ejercicio, usamos los tres puntos en el medio. Esto es útil para simplificar un poco la expresión factorial.
EJERCICIO 5
Simplifica la expresión $latex \frac{n!}{(n-2)!}$.
Solución
La expresión factorial en el numerador es mayor que la expresión factorial en el denominador, por lo que expandimos a n! parcialmente hasta que la expresión $latex (n-2)!$ aparezca:
$latex \frac{n!}{(n-2)!}=\frac{n(n-1)(n-2)!}{(n-2)!}$
Ahora, podemos cancelar los factores comunes:
$latex \frac{n(n-1)(n-2)!}{(n-2)!}=n(n-1)$
Podemos aplicar la propiedad distributiva para simplificar:
$latex n(n-1)={{n}^2}-n$
EJERCICIO 6
Simplifica la expresión $latex \frac{(k+1)!}{(k+3)!}$.
Solución
En este caso, el denominador es claramente mayor que el numerador, ya que el 3 está siendo sumado a n a diferencia del numerador que sólo está siendo sumado por 1.
Mantenemos al numerador sin ningún cambio mientras expandimos al denominador hasta que la expresión $latex (k+1)!$ aparezca:
$latex \frac{(k+1)!}{(k+3)!}= \frac{(k+1)!}{(k+3)(k+2)(k+1)!}$
Ahora, cancelamos los factores comunes:
$latex \frac{(k+1)!}{(k+3)(k+2)(k+1)!}=\frac{1}{(k+3)(k+2)}$
Multiplicamos los binomios en el denominador para terminar:
$latex \frac{1}{(k+3)(k+2)}=\frac{1}{{{k}^2}+5k+6}$
EJERCICIO 7
Simplifica la expresión $latex \frac{(n+2)!}{(n-1)!}$.
Solución
Aquí, el numerador es mayor, ya que estamos sumando 2 y en el denominador estamos restando 1. Entonces, expandimos parcialmente al numerador hasta que la expresión $latex (n-1)!$ aparezca:
$latex \frac{(n+2)!}{(n-1)!}= \frac{(n+2)(n+1)(n)(n-1)!}{(n-1)!}$
Simplificamos a $latex (n-1)!$ tanto en el numerador como en el denominador:
$latex \frac{(n+2)(n+1)(n)(n-1)!}{(n-1)!}=(n+2)(n+1)(n)$
Ahora, expandimos la expresión para simplificar:
$latex (n+2)(n+1)(n)={{n}^3}+3{{n}^2}+2n$
Ejercicios de factoriales para resolver
Usa los siguientes ejercicios para poner a prueba tu conocimiento sobre factoriales y sobre simplificación de factoriales. Resuelve los ejercicios, selecciona una respuesta y verifícala para comprobar que escogiste la correcta.
Véase también
¿Interesado en aprender más sobre expresiones algebraicas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
