Las circunferencias son formadas por un conjunto de puntos que se ubican a la misma distancia desde un punto fijo. El punto fijo es denominado el centro de la circunferencia y la distancia de los puntos es denominada el radio. La ecuación de la circunferencia con centro fuera del origen es encontrada usando la ecuación de una circunferencia que tiene un centro en el origen y luego aplicamos traslaciones verticales y horizontales.
A continuación, aprenderemos a encontrar ecuaciones para este tipo de circunferencias. Luego, veremos algunos ejercicios de práctica.
PRECÁLCULO
Relevante para…
Aplicar la ecuación de la circunferencia con centro fuera del origen.
PRECÁLCULO
Relevante para…
Aplicar la ecuación de la circunferencia con centro fuera del origen.
Circunferencias con centro fuera del origen
Para encontrar la ecuación de una circunferencia centrada fuera del origen, usamos la ecuación de una circunferencia que tiene un centro en el origen y luego aplicamos traslaciones verticales y horizontales.
Recordemos que la ecuación de una circunferencia con el centro en el origen es $latex {{x}^2}+{{y}^2}={{r}^2}$. Esta ecuación fue derivada usando el teorema de Pitágoras. Si es que reescribimos a esta ecuación usando el centro, tendríamos $latex {{(x-0)}^2}+{{(y-0)}^2}={{r}^2}$.
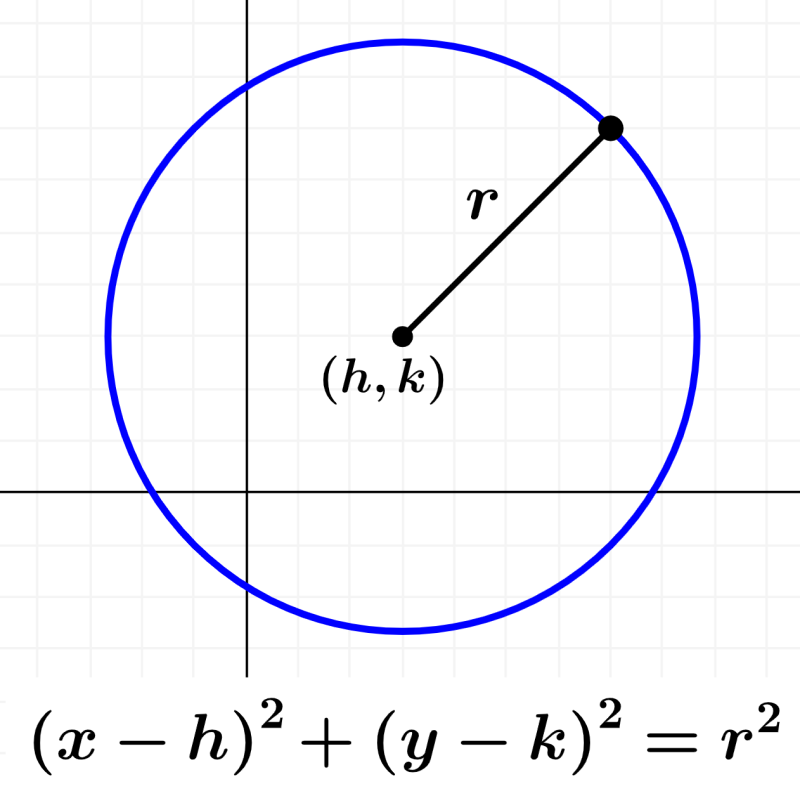
Ahora, consideremos la siguiente circunferencia:
Podemos ver que esta circunferencia tiene a su centro ubicado en el punto $latex (h, k)$. Entonces, si es que usamos la ecuación de la circunferencia con este centro, tenemos:
| $latex {{(x-h)}^2}+{{(y-k)}^2}={{r}^2}$ |
Esta es la ecuación de la circunferencia centrada fuera del origen, en donde r es el radio, $latex (x, y)$ es cualquier punto que se ubica en la circunferencia y $latex (h, k)$ son las coordenadas del centro de la circunferencia.
Ejercicios resueltos de ecuación de la circunferencia con centro fuera del origen
Los siguientes ejercicios facilitan el entendimiento de la aplicación de la ecuación de la circunferencia con centro fuera del origen. Intenta resolver los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
Encuentra el radio y el centro de la circunferencia $latex {{(x-2)}^2}+{{(x-3)}^2}=9$.
Solución
La ecuación general de la circunferencia es $latex {{(x-h)}^2}+{{(y-k)}^2}={{r}^2}$, en donde $latex (h, k)$ es el centro y r es el radio. Comparando esta ecuación con la ecuación dada, tenemos:
$latex {{r}^2}=9$
$latex r=3$
$latex h=2$
$latex k=3$
Entonces, el radio de la circunferencia es 3 y el centro es (2, 3).
EJERCICIO 2
¿Cuál es el radio y el centro de una circunferencia que tiene la ecuación $latex {{(x+4)}^2}+{{(y-5)}^2}=16$?
Solución
Recordamos que la ecuación general de la circunferencia es $latex {{(x-h)}^2}+{{(y-k)}^2}={{r}^2}$. Esta ecuación nos indica que $latex (h, k)$ es el centro y r es el radio de la circunferencia. Entonces, podemos determinar lo siguiente:
$latex {{r}^2}=16$
$latex r=4$
$latex h=-4$
$latex k=5$
Entonces, el radio de la circunferencia es 4 y el centro es (-4, 5).
EJERCICIO 3
Encuentra la ecuación de la circunferencia que tiene el centro en el punto (2, -3) y tiene un radio de 4.
Solución
Reemplazamos los valores $latex h=2$, $latex k=-3$ y $latex r=4$ en la ecuación general $latex {{(x-h)}^2}+{{(y-k)}^2}={{r}^2}$. Entonces, tenemos:
$latex {{(x-h)}^2}+{{(y-k)}^2}={{r}^2}$
$latex {{(x-2)}^2}+{{(y-(-3))}^2}={{4}^2}$
$latex {{(x-2)}^2}+{{(y+3)}^2}=16$
EJERCICIO 4
Encuentra la ecuación de la circunferencia que tiene el centro en el punto (-1, 2) y en la que el punto (2, 6) es parte de la circunferencia.
Solución
En este caso, conocemos los valores $latex h=-1$, $latex k=2$. Sin embargo, no conocemos el radio de la circunferencia. Para esto podemos usar la fórmula de la distancia entre dos puntos, ya que esta distancia representa al radio. Entonces, tenemos:
$latex d=\sqrt{{{(x_{2}-x_{1})}^2}+{{(y_{2}-y_{1})}^2}}$
$latex d=\sqrt{{{(2-(-1))}^2}+{{(6-2)}^2}}$
$latex d=\sqrt{{{3}^2}+{{4}^2}}$
$latex d=\sqrt{9+16}$
$latex d=\sqrt{25}$
$latex d=5$
El radio de la circunferencia es $latex r=5$. Usamos la ecuación general de la circunferencia con estos valores:
$latex {{(x-h)}^2}+{{(y-k)}^2}={{r}^2}$
$latex {{(x-(-1))}^2}+{{(y-2)}^2}={{5}^2}$
$latex {{(x+1)}^2}+{{(y-2)}^2}=25$
Ejercicios de ecuación de la circunferencia con centro fuera del origen para resolver
Resuelve los siguientes ejercicios usando lo aprendido sobre la ecuación de la circunferencia con centro fuera del origen. Puedes mirar los ejercicios resueltos de arriba en caso de necesitar ayuda.
Véase también
¿Interesado en aprender más sobre ecuaciones de circunferencias? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
