Una circunferencia es el conjunto de puntos que son equidistantes desde un punto fijo. El punto fijo es llamado el centro y la distancia desde el centro hasta un punto en la circunferencia es llamado el radio. La ecuación de la circunferencia con centro en el origen es encontrada usando el teorema de Pitágoras en el plano cartesiano.
A continuación, derivaremos esta ecuación y la aplicaremos para resolver algunos ejercicios de práctica.
PRECÁLCULO
Relevante para…
Aplicar la ecuación de la circunferencia con centro en el origen.
PRECÁLCULO
Relevante para…
Aplicar la ecuación de la circunferencia con centro en el origen.
Circunferencias centradas en el origen
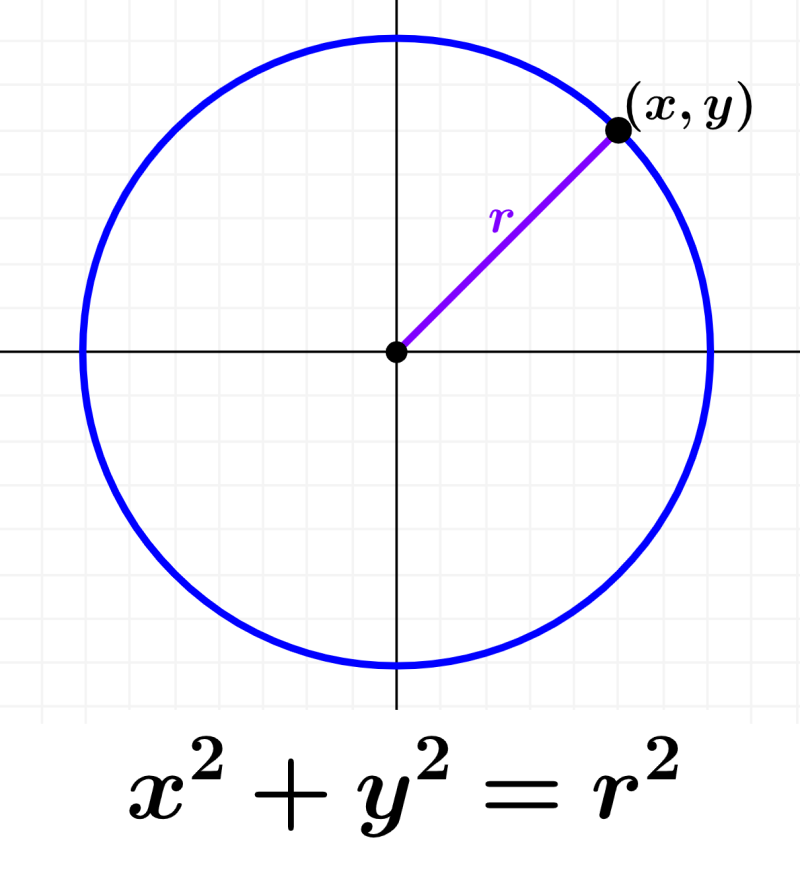
Para encontrar la ecuación de una circunferencia centrada en el origen, podemos usar el plano cartesiano junto con el teorema de Pitágoras. Trazamos una circunferencia como en el siguiente diagrama:
Vemos que la circunferencia tiene su centro en el punto (0, 0). Trazamos el punto (x, y) que se ubica en la circunferencia. Además, también trazamos un triángulo rectángulo que conecta al centro con el punto (x, y).
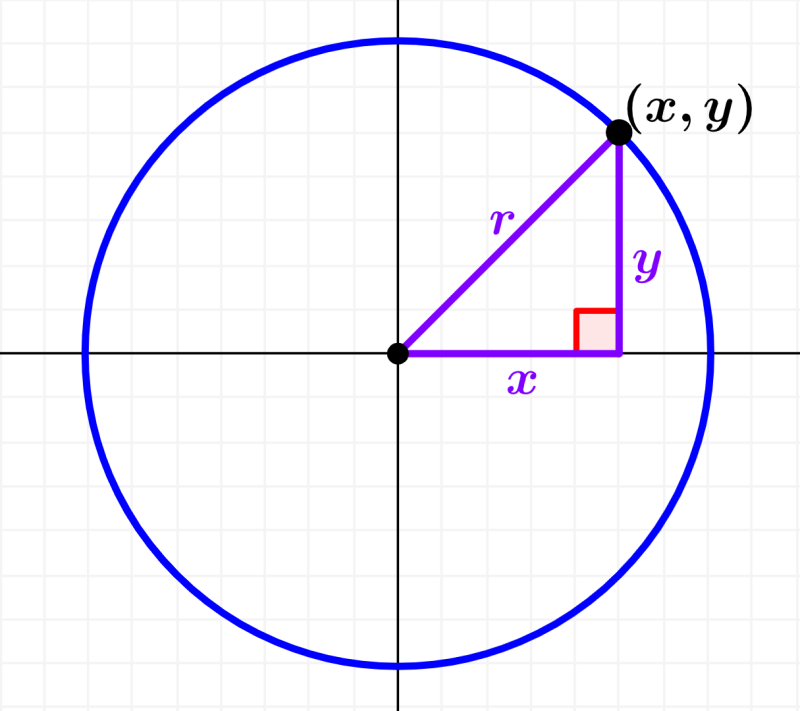
La base del triángulo es igual a la coordenada en x del punto y la altura es igual a la coordenada en y. También observamos que la hipotenusa del triángulo es igual al radio. Entonces, podemos formar la siguiente ecuación:
| $latex {{x}^2}+{{y}^2}={{r}^2}$ |
Esta es la ecuación de la circunferencia centrada en el origen, en donde r es el radio y (x, y) es cualquier punto que se ubica en la circunferencia.
Ejercicios resueltos de ecuación de la circunferencia con centro en el origen
Los siguientes ejercicios ponen en práctica el uso de la ecuación de la circunferencia con centro en el origen. Cada ejercicio tiene su respectiva solución, pero es recomendable que intentes resolver los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
Encuentra el radio de la circunferencia representada por la ecuación $latex {{x}^2}+{{y}^2}=4$.
Solución
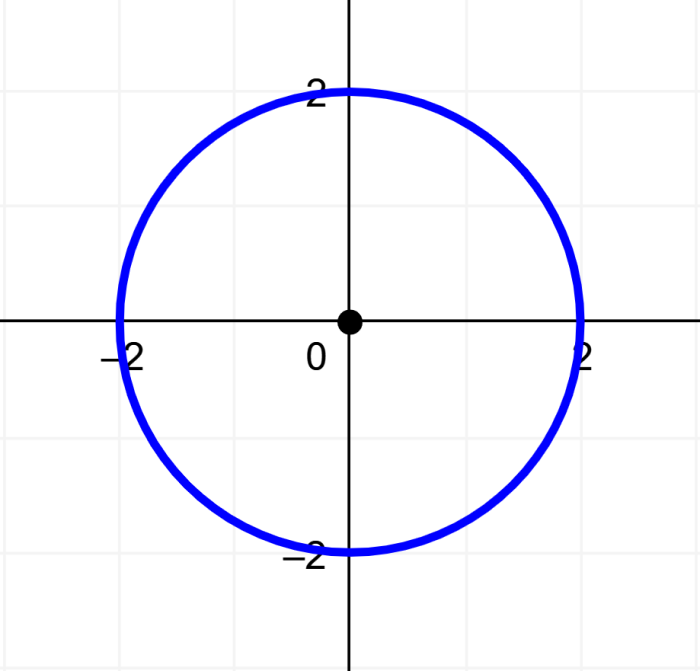
La siguiente es la gráfica de esta ecuación:
Sabemos que una circunferencia tiene la ecuación general $latex {{x}^2}+{{y}^2}={{r}^2}$. Comparando la ecuación general con la ecuación de la circunferencia dada, sabemos que tenemos:
$latex {{r}^2}=4$
$latex r=2$
Entonces, el radio de la circunferencia es 2.
EJERCICIO 2
Encuentra la ecuación de la circunferencia que tiene un radio de 5 y está centrada en el origen.
Solución
Usamos la ecuación general de la circunferencia y reemplazamos el valor $latex r=5$. Entonces, tenemos:
$latex {{x}^2}+{{y}^2}={{r}^2}$
$latex {{x}^2}+{{y}^2}={{5}^2}$
$latex {{x}^2}+{{y}^2}=25$
EJERCICIO 3
Encuentra la ecuación de la circunferencia que pasa a través del punto (3, 5).
Solución
El punto (3, 5) se ubica en la circunferencia. Esto significa que tenemos las coordenadas $latex x=3$ y $latex y=5$. Entonces, usamos la ecuación de la circunferencia con estas coordenadas para encontrar el radio de la circunferencia:
$latex {{x}^2}+{{y}^2}={{r}^2}$
$latex {{3}^2}+{{5}^2}={{r}^2}$
$latex 9+25={{r}^2}$
$latex {{r}^2}=34$
Ahora, reemplazamos a este valor en la ecuación general para obtener la ecuación para esta circunferencia:
$latex {{x}^2}+{{y}^2}={{r}^2}$
$latex {{x}^2}+{{y}^2}=34$
EJERCICIO 4
Determina si es que el punto (5, 6) está en la circunferencia $latex {{x}^2}+{{y}^2}=61$.
Solución
Usamos la ecuación dada con las coordenadas del punto (5, 6). Entonces, reemplazamos los valores $latex x=5$ y $latex y=6$ y verificamos si es que la ecuación es verdadera:
$latex {{x}^2}+{{y}^2}=61$
$latex {{5}^2}+{{6}^2}=61$
$latex 25+36=61$
$latex 61=61$
La ecuación sí es verdadera. Esto significa que el punto (5, 6) sí está en la circunferencia dada.
EJERCICIO 5
Determina si es que el punto (7, 8) está en la circunferencia $latex {{x}^2}+{{y}^2}=94$.
Solución
Reemplazamos los valores $latex x=7$ y $latex y=8$ en la ecuación de la circunferencia dada y comprobamos que la ecuación sea verdadera:
$latex {{x}^2}+{{y}^2}=94$
$latex {{7}^2}+{{8}^2}=94$
$latex 49+64=94$
$latex 113=94$
La ecuación no es verdadera. Esto significa que el punto (7, 8) no es parte de la circunferencia dada.
Ejercicios de ecuación de la circunferencia con centro en el origen para resolver
Usa lo aprendido sobre la ecuación de la circunferencia con centro en el origen para resolver los siguientes ejercicios. Si necesitas ayuda con esto, puedes mirar los ejercicios resueltos de arriba.
Véase también
¿Interesado en aprender más sobre ecuaciones de circunferencias? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
