La circunferencia está formada por un conjunto de puntos que se ubican a una distancia constante desde un punto fijo. La distancia constante es llamada el radio de la circunferencia y el punto fijo es llamado el centro. La ecuación de la circunferencia en su forma general es obtenida al expandir a la ecuación usada cuando la circunferencia tiene un centro fuera del origen.
A continuación, conoceremos la ecuación de la circunferencia en su forma general y la usaremos en algunos ejercicios de práctica.
PRECÁLCULO
Relevante para…
Conocer la ecuación de la circunferencia en su forma general.
PRECÁLCULO
Relevante para…
Conocer la ecuación de la circunferencia en su forma general.
Forma general de la ecuación de una circunferencia
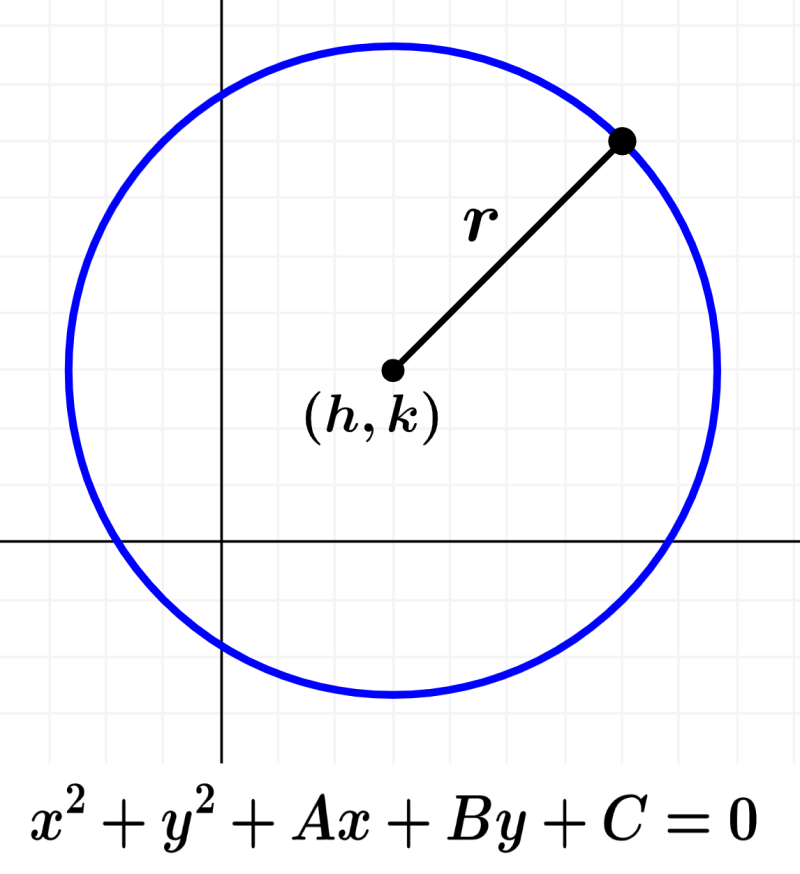
Recordemos que una circunferencia con centro en el punto $latex (h, k)$ y con radio r puede ser escrita como la siguiente ecuación:
$latex {{(x-h)}^2}+{{(y-k)}^2}={{r}^2}$
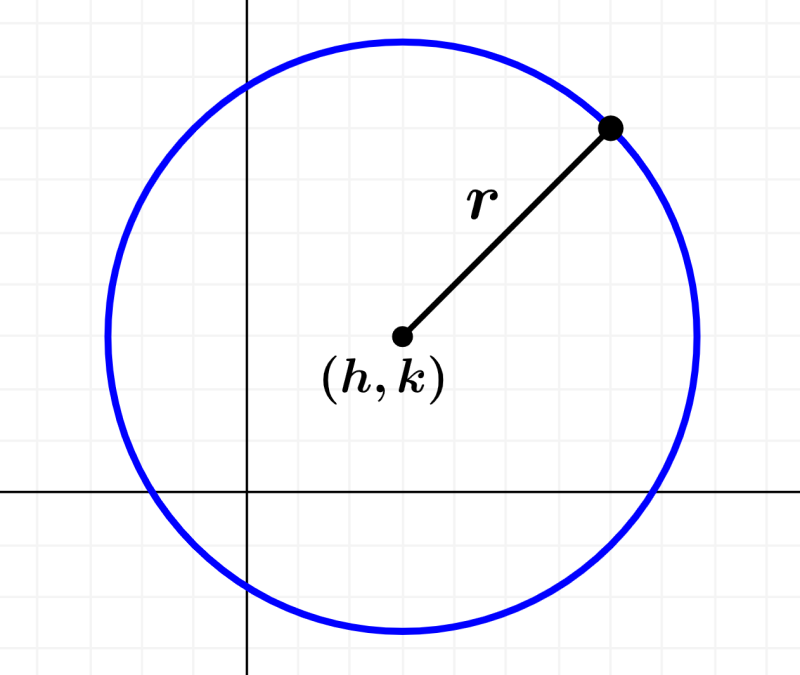
Si es que expandimos los paréntesis elevados al cuadrado, tenemos:
$${{x}^2}+{{y}^2}-2hx-2ky+{{h}^2}+{{k}^2}-{{r}^2}=0$$
Si es que realizamos las sustituciones $latex A=-2h$, $latex B=-2k$, $latex C={{h}^2}+{{k}^2}-{{r}^2}$ en la ecuación expandida, tenemos:
| $latex {{x}^2}+{{y}^2}+Ax+Bx+C=0$ |
Esta es la ecuación de la circunferencia en su forma general. Si es que tenemos una ecuación de una circunferencia en este forma, podemos obtener el centro y el radio de la circunferencia al usar las siguientes sustituciones:
$latex A=-2h$ $latex B=-2k$ $latex C={{h}^2}+{{k}^2}-{{r}^2}$
Al despejar a estas expresiones en términos de h, k y r, tenemos:
$latex h=-\frac{A}{2}$
$latex k=-\frac{B}{2}$
$latex {{r}^2}={{h}^2}+{{k}^2}-C$
$latex {{r}^2}={{(-\frac{A}{2})}^2}+{{(-\frac{B}{2})}^2}-C$
$latex {{r}^2}=\frac{{{A}^2}+{{B}^2}-4C}{4}$
En la ecuación original, sabemos que el centro de la circunferencia es el punto $latex (h, k)$. Esto significa que el centro de la circunferencia en su forma general es $latex (-\frac{A}{2}, -\frac{B}{2})$ y el radio es $latex r=\sqrt{\frac{{{A}^2}+{{B}^2}-4C}{4}}$
Ejercicios resueltos de ecuación de la circunferencia en su forma general
Los siguientes ejercicios muestran el proceso usado para resolver ejercicios de ecuación de la circunferencia en su forma general. Es recomendable que intentes resolver los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
Si es que tenemos la circunferencia $latex {{x}^2}+{{y}^2}-2x+4y-4=0$, ¿cuál es su centro y su radio?
Solución
La siguiente es la gráfica de esta ecuación:
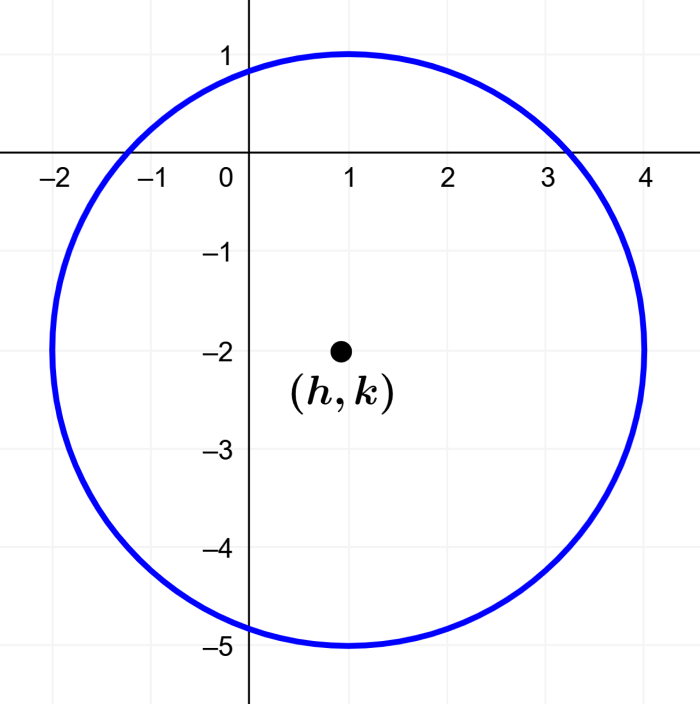
Usando las expresiones derivadas arriba, sabemos que el centro de una circunferencia en su forma general está dado por:
$latex (-\frac{A}{2}, -\frac{B}{2})=(-\frac{-2}{2}, -\frac{4}{2})=(1, -2)$
y el radio está dado por:
$latex r=\sqrt{\frac{{{A}^2}+{{B}^2}-4C}{4}}$
$latex =\sqrt{\frac{{{(-2)}^2}+{{4}^2}-4(-4)}{4}}$
$latex =\sqrt{\frac{4+16+16}{4}}$
$latex =\sqrt{\frac{36}{4}}$
$latex =\frac{6}{2}=3$
Entonces, el radio de la circunferencia es 3 y el centro es el punto (1, -2).
EJERCICIO 2
Encuentra el centro y el radio de la circunferencia $latex {{x}^2}+{{y}^2}+6x-2y+3=0$.
Solución
Usamos las expresiones dadas e identificamos los respectivos parámetros. Entonces, el centro de una circunferencia en su forma general está dado por:
$latex (-\frac{A}{2}, -\frac{B}{2})=(-\frac{6}{2}, -\frac{-2}{2})=(-3, 1)$
y el radio está dado por:
$latex r=\sqrt{\frac{{{A}^2}+{{B}^2}-4C}{4}}$
$latex =\sqrt{\frac{{{6}^2}+{{(-2)}^2}-4(3)}{4}}$
$latex =\sqrt{\frac{36+4-12}{4}}$
$latex =\sqrt{\frac{28}{4}}$
$latex =\sqrt{7}$
Entonces, el radio de la circunferencia es $latex \sqrt{7}$ y el centro es el punto (-3, 1).
EJERCICIO 3
Encuentra la ecuación de la circunferencia en su forma general que tiene un radio de 2 y un centro en (2, 2).
Solución
Para encontrar la ecuación de la circunferencia en su forma general, tenemos que encontrar el valor de las constantes A, B y C. Entonces, vamos a usar las expresiones dadas arriba recordando que el centro de la circunferencia es $latex (h, k)$:
$latex A=-2h=-2(2)=-4$
$latex B=-2k=-2(2)=-4$
$latex C={{h}^2}+{{k}^2}-{{r}^2}$
$latex C={{2}^2}+{{2}^2}-{{2}^2}$
$latex C=4+4-4=4$
Ahora, formamos la ecuación de la circunferencia con los valores encontrados:
$latex {{x}^2}+{{y}^2}+Ax+By+C=0$
$latex {{x}^2}+{{y}^2}-4x-4y+4=0$
EJERCICIO 4
¿Cuál es la ecuación de la circunferencia que tiene un radio de 4 y un centro en (3, -2)?
Solución
Encontramos los valores de las constantes A, B y C usando las expresiones dadas arriba:
$latex A=-2h=-2(3)=-6$
$latex B=-2k=-2(-2)=4$
$latex C={{h}^2}+{{k}^2}-{{r}^2}$
$latex C={{3}^2}+{{(-2)}^2}-{{4}^2}$
$latex C=9+4-16=-3$
Ahora, formamos la ecuación de la circunferencia con los valores encontrados:
$latex {{x}^2}+{{y}^2}+Ax+By+C=0$
$latex {{x}^2}+{{y}^2}-6x+4y-3=0$
Ejercicios de ecuación de la circunferencia en su forma general para resolver
Resuelve los siguientes ejercicios usando lo aprendido sobre ecuaciones de la circunferencia en su forma general. Si necesitas ayuda con esto, puedes mirar los ejercicios resueltos de arriba.
Véase también
¿Interesado en aprender más sobre ecuaciones de circunferencias? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
