La circunferencia es definida como el conjunto de puntos que son equidistantes desde un punto fijo llamado el centro. La distancia constante desde el centro hasta cualquier punto en la circunferencia es denominada el radio. Es posible encontrar la ecuación de la circunferencia si es que conocemos tres puntos por los que pasa. Esto requiere reemplazar los valores conocidos en la ecuación general de la circunferencia y formar un sistema de tres ecuaciones. Los valores de las constantes faltantes pueden ser encontrados al resolver el sistema de ecuaciones.
A continuación, veremos algunos ejemplos del proceso usado.
PRECÁLCULO
Relevante para…
Encontrar la ecuación de la circunferencia que pasa por tres puntos.
PRECÁLCULO
Relevante para…
Encontrar la ecuación de la circunferencia que pasa por tres puntos.
Encontrar la ecuación de la circunferencia usando tres puntos
La ecuación de una circunferencia puede ser encontrada usando las coordenadas de tres puntos que se ubican en la circunferencia.
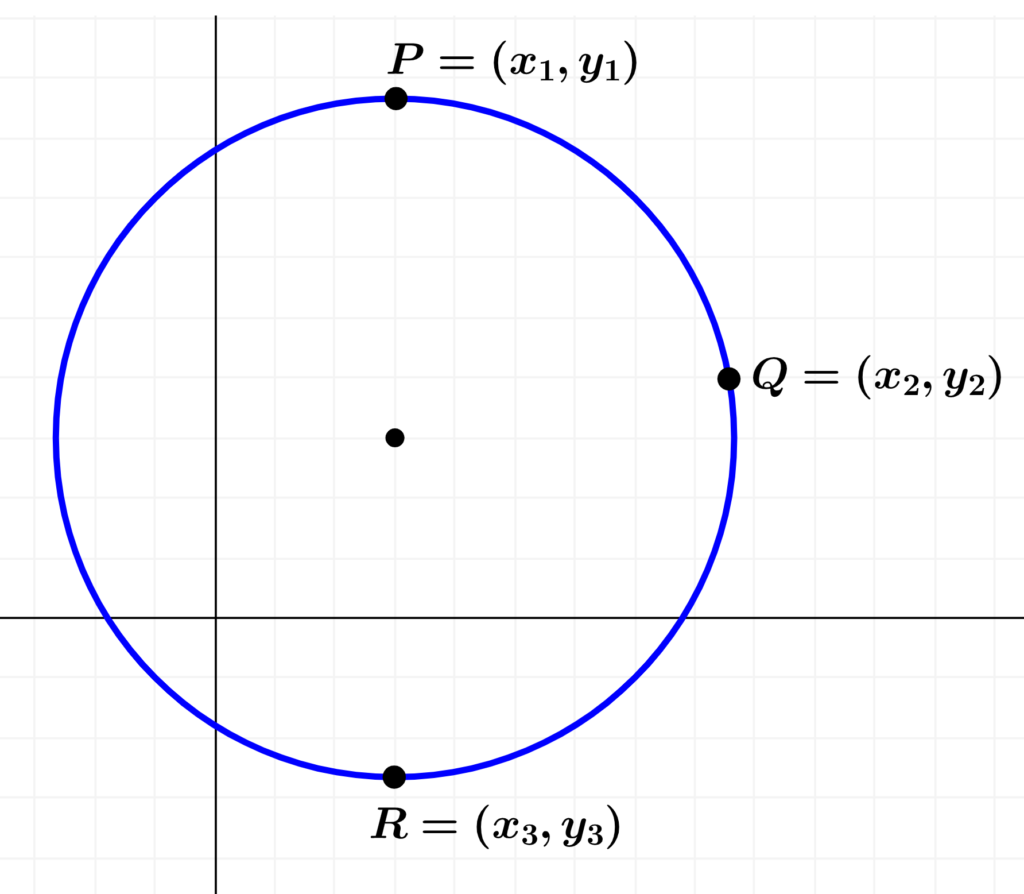
Supongamos que tenemos los puntos $latex P=(x_{1}, ~y_{1})$, $latex Q=(x_{2}, ~y_{2})$ y $latex R=(x_{3}, ~y_{3})$. Podemos observar esto en el siguiente diagrama:
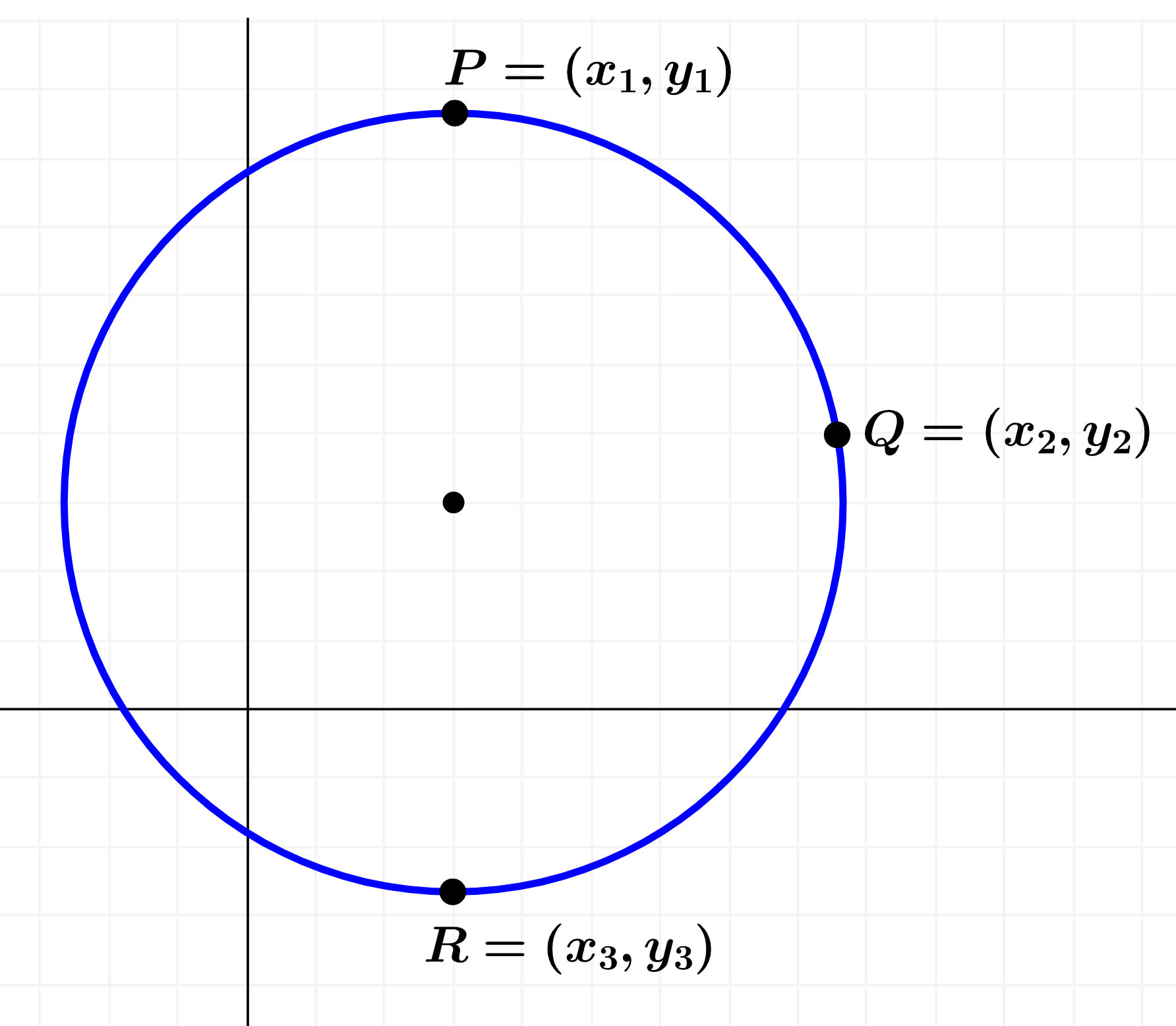
Podemos escribir a la ecuación de una circunferencia en la siguiente forma general:
$latex {{x}^2}+{{y}^2}+2ax+2by+c=0$ (1)
Podemos sustituir a los puntos $latex P=(x_{1}, ~y_{1})$, $latex Q=(x_{2}, ~y_{2})$ y $latex R=(x_{3}, ~y_{3})$ en la ecuación dada para formar diferentes ecuaciones, una para cada par de coordenadas. Entonces, tenemos:
$latex {{x_{1}}^2}+{{y_{1}}^2}+2ax_{1}+2by_{1}+c=0$ (2)
$latex {{x_{2}}^2}+{{y_{2}}^2}+2ax_{2}+2by_{2}+c=0$ (3)
$latex {{x_{3}}^2}+{{y_{3}}^2}+2ax_{3}+2by_{3}+c=0$ (4)
Con las ecuaciones (2), (3) y (4) formamos un sistema de ecuaciones y encontramos los valores de las constantes a, b y c. Luego, sustituimos estos valores en la ecuación (1) para encontrar la ecuación de la circunferencia requerida.
Ejercicios resueltos de ecuación de la circunferencia que pasa por tres puntos
Los siguientes ejercicios pueden ser usados para entender el proceso usado para encontrar la ecuación de una circunferencia si es que conocemos las coordenadas de tres puntos diferentes que son parte de la circunferencia.
EJERCICIO 1
Encuentra la ecuación de la circunferencia que pasa por los puntos (1, 0), (-1, 0) y (0, 1).
Solución
La ecuación de la circunferencia en su forma general es $latex {{x}^2}+{{y}^2}+2ax+2ay+c=0$. Usando las coordenadas de los puntos dados, podemos formar las siguientes ecuaciones:
$latex 1+2a+c=0$ (1)
$latex 1-2a+c=0$ (2)
$latex 1+2b+c=0$ (3)
Podemos sustraer la ecuación (2) de la ecuación (1) para obtener $latex 4a=0$. Esto significa que $latex a=0$.
Al reemplazar el valor $latex a=0$ en la ecuación (1), obtenemos $latex c=-1$. Finalmente, si es que reemplazamos el valor $latex c=-1$ en la ecuación (3), tenemos $latex b=0$.
Si es que sustituimos los valores de a, b y c en la ecuación general, tenemos:
$latex {{x}^2}+{{y}^2}+2ax+2ay+c=0$
$latex {{x}^2}+{{y}^2}+2(0)x+2(0)y+-1=0$
$latex {{x}^2}+{{y}^2}-1=0$
$latex {{x}^2}+{{y}^2}=1$
EJERCICIO 2
¿Cuál es la ecuación de la circunferencia que pasa a través de los puntos (1, -6), (2, 1) y (5, 2)? Determina la longitud de su radio y las coordenadas de su centro.
Solución
La siguiente es la ecuación de una circunferencia en su forma general:
$latex {{x}^2}+{{y}^2}+2ax+2ay+c=0$
Usamos esta ecuación con las coordenadas de los puntos dados para formar un sistema de tres ecuaciones.
Usando el punto (1, -6), tenemos:
$latex 1+36+2a-12b+c=0$
$latex 2a-12b+c=-37$ (1)
Usando el punto (2, 1), tenemos:
$latex 4+1+4a+2b+c=0$
$latex 4a+2b+c=-5$ (2)
Usando el punto (5, 2), tenemos:
$latex 25+4+10a+4b+c=0$
$latex 10a+4b+c=-29$ (3)
Si es que restamos la ecuación (1) de la (2), tenemos:
$latex 2a+14b=32$
⇒ $latex a+7b=16$ (4)
Ahora, si es que restamos la ecuación (1) de la (3), obtenemos:
$latex 8a+16b=8$
⇒ $latex a+2b=1$ (5)
Al resolver las ecuaciones (4) y (5), obtenemos $latex a=-5$ y $latex b=3$. Finalmente, usando los valores de a y b en la ecuación (2), obtenemos $latex c=9$.
Si es que sustituimos los valores de a, b y c en la ecuación general, tenemos:
$latex {{x}^2}+{{y}^2}+2ax+2ay+c=0$
$latex {{x}^2}+{{y}^2}+2(-5)x+2(3)y+9=0$
$latex {{x}^2}+{{y}^2}-10x+6x+9=0$
Las coordenadas de su centro son $latex (-a, -b)=(5, -3)$ y el radio es $latex \sqrt{{{a}^2}+{{b}^2}-c}=\sqrt{25+9-9}=5$.
Véase también
¿Interesado en aprender más sobre ecuaciones de circunferencias? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
