El logaritmo natural de x+1, también indicado como ln(x+1), es el logaritmo de x+1 en base e (número de Euler). La derivada del logaritmo natural de x+1 es igual a uno sobre x+1, 1/(x+1). Esta derivada se puede encontrar usando la regla de la cadena o con diferenciación implícita.
En este artículo, veremos cómo obtener la derivada de ln(x+1). Aprenderemos sobre demostraciones y comparaciones gráficas de ln(x+1) y su derivada.
CÁLCULO
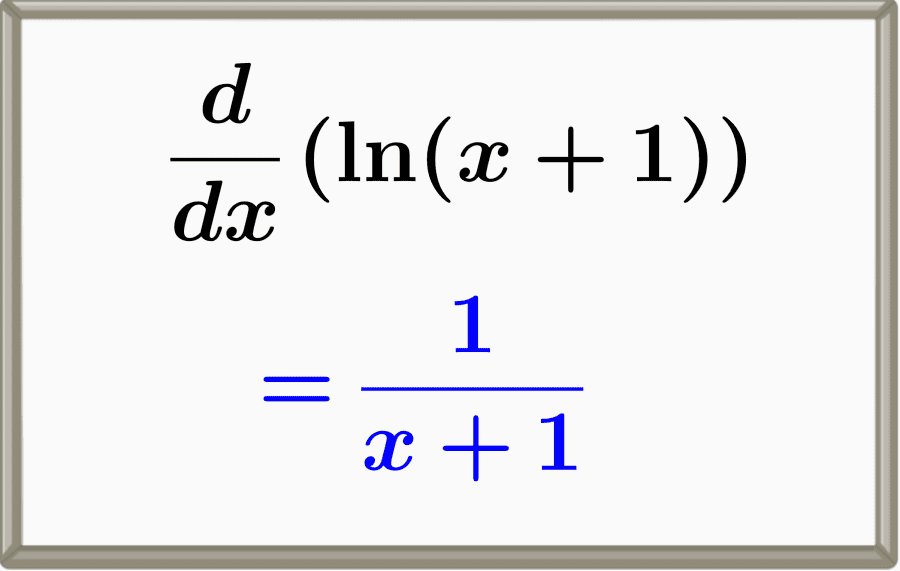
Relevante para…
Aprender a encontrar la derivada del logaritmo natural de x+1.
CÁLCULO
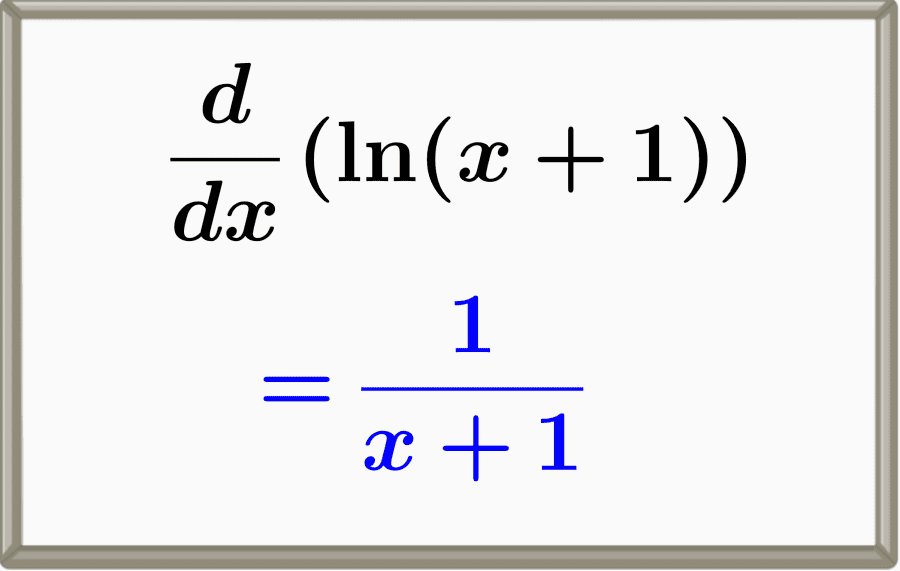
Relevante para…
Aprender a encontrar la derivada del logaritmo natural de x+1.
Demostraciones de la derivada del logaritmo natural de x+1
A continuación se enumeran las demostraciones de la derivada de \(\ln{(x+1)}\). Estas demostraciones también pueden servir como los métodos principales para derivar esta función.
Demostración de la derivada de ln(x+1) usando la fórmula de la regla de la cadena
En el proceso de derivada del logaritmo natural de x+1, se utiliza la fórmula de la regla de la cadena para verificar la fórmula de la derivada del logaritmo natural de x+1 ya que está formada por estas dos funciones.
La función logarítmica natural será la función exterior f(u) en la función compuesta ln(x+1), mientras que el binomio x+1 será la función interior g(x).
Puede revisar la fórmula de la regla de la cadena consultando este artículo: Regla de la Cadena. También puede consultar este artículo para ver la prueba de la derivada del logaritmo natural usando límites: Derivada de Logaritmo Natural (ln(x)).
Tenemos la función
$$ F(x) = \ln{(x+1)}$$
Podemos averiguar las dos funciones que forman F(x). Hay una función logarítmica natural y un monomio en este caso. La función externa se puede configurar de la siguiente manera.
$$ f(u) = \ln{(u)}$$
en donde
$$ u = x+1$$
Al establecer el binomio x+1 como la función interna de f(u) denotándolo como g(x), tenemos
$$ f(u) = f(g(x))$$
$$ g(x) = x+1$$
$$ u = g(x)$$
Derivando la función externa f(u) usando la derivada del logaritmo natural en términos de u, tenemos
$$ f(u) = \ln{(u)}$$
$$ f'(u) = \frac{1}{u}$$
Derivando la función interna g(x) usando la regla de potencia ya que es un monomio, tenemos
$$ g(x) = x+1$$
$$ g'(x) = 1$$
Multiplicando algebraicamente la derivada de la función exterior $latex f'(u)$ por la derivada de la función interior $latex g'(x)$, tenemos
$$ \frac{dy}{dx} = f'(u) \cdot g'(x)$$
$$ \frac{dy}{dx} = \left(\frac{1}{u} \right) \cdot (1)$$
Sustituyendo u en f‘(u), tenemos
$$ \frac{dy}{dx} = \left(\frac{1}{(x+1)} \right) \cdot (1)$$
$$ \frac{dy}{dx} = \frac{1}{x+1}$$
Como resultado, llegamos a la fórmula de la derivada ln(x+1).
$$ \frac{d}{dx} \ln{(x+1)} = \frac{1}{x+1}$$
Demostración de la derivada de ln(x+1) usando diferenciación implícita
Se recomienda aprender/repasar las derivadas de funciones exponenciales y la diferenciación implícita para esta demostración.
Tenemos la ecuación
$$ y = \ln{(x+1)}$$
En forma logarítmica general, es
$$ \log_{e}{(x+1)} = y$$
Y en forma exponencial es
$$ e^y = x+1$$
Derivando implícitamente la forma exponencial en términos de x, tenemos
$$ e^y = x+1$$
$$ \frac{d}{dx} (e^y) = \frac{d}{dx} (x+1) $$
$$ e^y \cdot \frac{dy}{dx} = 1 $$
Aislando a \( \frac{dy}{dx} \), tenemos
$$ \frac{dy}{dx} = \frac{1}{e^y} $$
Recordemos que \( y = \ln{(x+1)} \). Sustituyendo esto en la y de nuestra derivada, tenemos
$$ \frac{dy}{dx} = \frac{1}{e^{(\ln{(x+1)})}} $$
Simplificando y aplicando una propiedad de logaritmos, tenemos
$$ \frac{dy}{dx} = \frac{1}{x+1} $$
Evaluando, ahora tenemos la derivada de \( y = \ln{(x+1)} \).
$$ y’ = \frac{1}{x+1} $$
Gráfica de ln(x+1) vs. su derivada
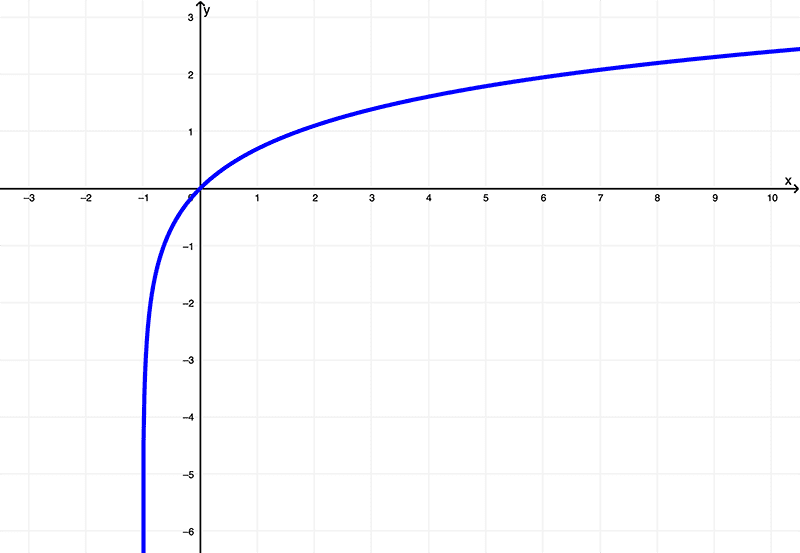
Tenemos la función
$$ f(x) = \ln{(x+1)}$$
y su gráfica es
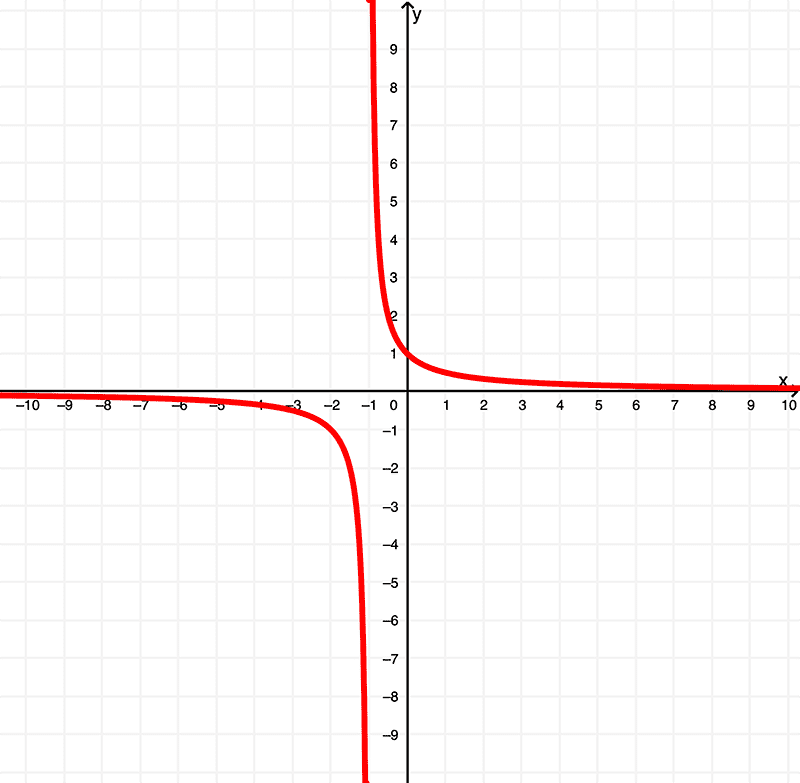
Y como aprendimos anteriormente, al derivar \(f(x) = \ln{(x+1)}\), tenemos
$$ f'(x) = \frac{1}{x+1}$$
que se ilustra gráficamente como
Ilustrando ambas gráficas en una, tenemos
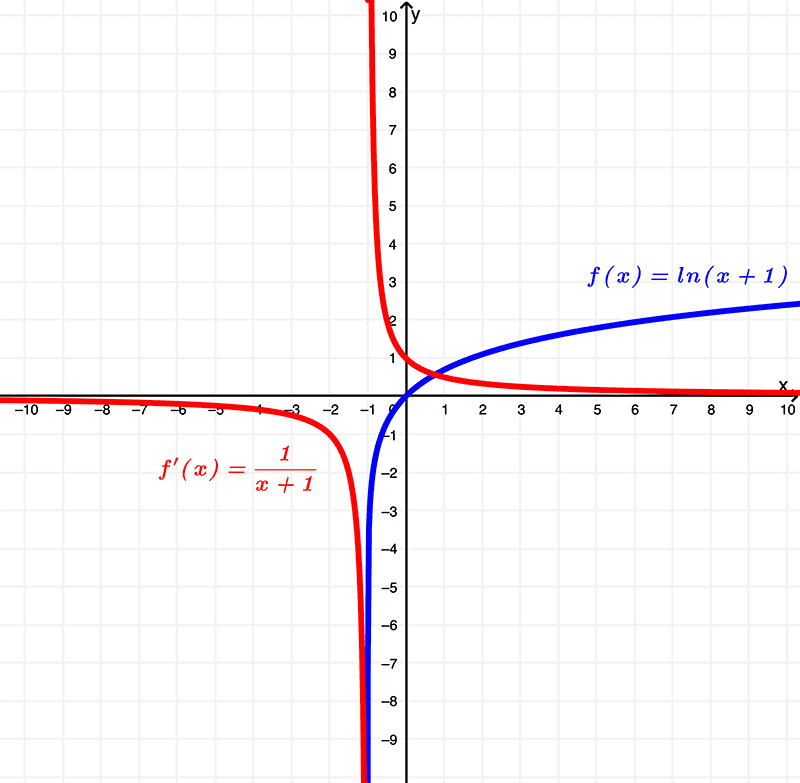
Al examinar las diferencias entre estas funciones usando estos gráficos, puedes ver que la función original \(f(x) = \ln{(x+1)}\) tiene un dominio de
\( (-1,\infty) \) o \( x | x > -1 \)
y se encuentra dentro del rango de
\( (-\infty, \infty) \) o todos los números reales
mientras que la derivada \(f'(x) = \frac{1}{x+1}\) tiene un dominio de
\( (-\infty,-1) \cup (-1,\infty) \) o \( x | x \neq -1 \)
que se encuentra dentro del rango de
\( (-\infty,0) \cup (0,\infty) \) o \( y | y \neq 0 \)
Véase también
¿Interesado en aprender más sobre derivadas de funciones logarítmicas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
