El primer término de una progresión aritmética puede ser encontrado usando la fórmula del término general de una progresión aritmética. Generalmente, necesitamos conocer el valor de la diferencia común y el valor y posición de uno de los términos de la progresión.
A continuación, aprenderemos a encontrar el primer término de una progresión aritmética usando una fórmula. Luego, aplicaremos esa fórmula para resolver algunos ejercicios de práctica.
ÁLGEBRA
Relevante para…
Aprender a encontrar el primer término de una progresión aritmética.
ÁLGEBRA
Relevante para…
Aprender a encontrar el primer término de una progresión aritmética.
Pasos para encontrar el primer término de una progresión aritmética
Las progresiones aritméticas se caracterizan porque cada término es formado al sumar un valor específico al término previo. El valor que es sumado es llamado la diferencia común.
Por ejemplo, la progresión 2, 4, 6, 8, 10, …, es formada al sumar 2 a cada término para obtener el siguiente. Es decir, la diferencia común es 2.
La fórmula para encontrar el término general de una progresión aritmética es la siguiente:
$$a_{n}=a+(n-1)d$$
en donde,
- $latex a$ es el primer término de la progresión.
- $latex d$ es la diferencia común.
- $latex n $ es la posición del término.
Podemos encontrar al primer término reescribiendo a la fórmula de la siguiente forma:
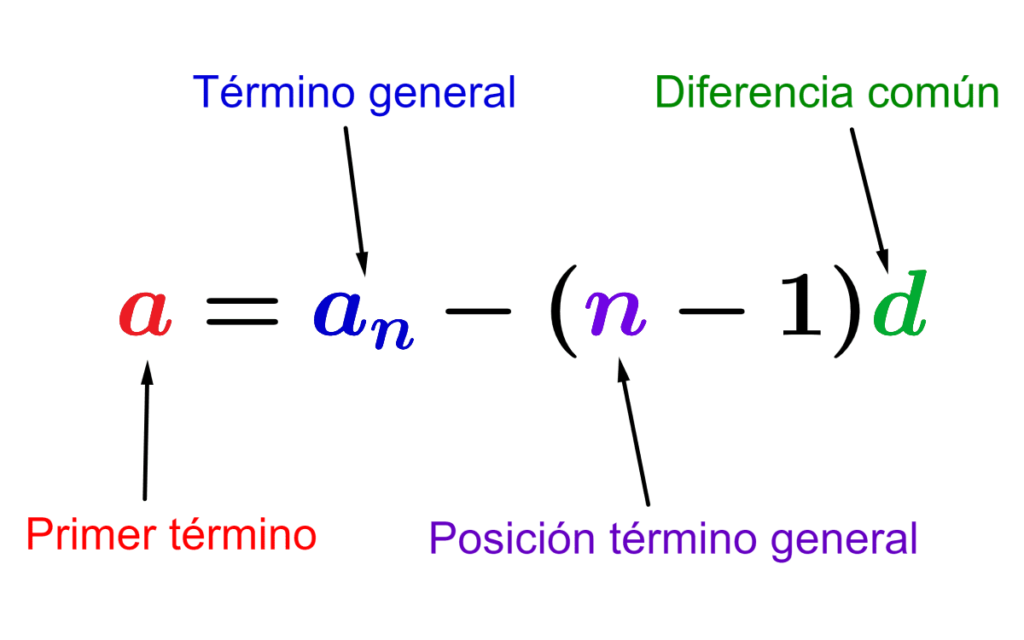
$$a=a_{n}-(n-1)d$$
Entonces, seguimos los siguientes pasos:
1. Encontrar la diferencia común.
La diferencia común es encontrada al restar a cualquier término de la progresión por su término previo.
2. Identificar al valor de cualquier término en la progresión y su posición.
La posición del término es el valor de $latex n$.
3. Usar la fórmula del primer término.
Sustituir los valores de los pasos 1 y 2 en la fórmula $latex a=a_{n}-(n-1)d$.
Ejemplos resueltos de primer término de progresiones aritméticas
EJEMPLO 1
Si es que el término 5 de una progresión aritmética es igual a 12 y la diferencia común es igual a 2, encuentra el valor del primer término.
Solución
En este caso, conocemos los valores de un término y la diferencia común directamente. Entonces, podemos observar lo siguiente:
- $latex a_{n}=a_{5}=12$
- $latex n=5$
- $latex d=2$
Ahora, podemos usar estos valores en la fórmula del primer término de una progresión aritmética:
$latex a=a_{n}-(n-1)d$
$latex a=12-(5-1)2$
$latex a=12-(4)2$
$latex a=12-8$
$latex a=4$
EJEMPLO 2
Encuentra el primer término de una progresión aritmética en la que el término 7 tiene un valor de 20 y la diferencia común es -2.
Solución
Similar al ejemplo anterior, conocemos los valores de un término y la diferencia común de la progresión. Entonces, tenemos:
- $latex a_{n}=a_{7}=20$
- $latex n=7$
- $latex d=-2$
En este caso, tenemos una diferencia común negativa, pero la fórmula del primer término aplica en cualquier caso:
$latex a=a_{n}-(n-1)d$
$latex a=20-(7-1)(-2)$
$latex a=20-(6)(-2)$
$latex a=20+12$
$latex a=32$
EJEMPLO 3
Si es que la diferencia común de una progresión aritmética es 6 y el término 12 es igual a 26, encuentra el valor del primer término.
Solución
Podemos observar la siguiente información:
- $latex a_{n}=a_{12}=26$
- $latex n=12$
- $latex d=6$
Entonces, usando estos valores en la fórmula del primer término, tenemos:
$latex a=a_{n}-(n-1)d$
$latex a=26-(12-1)6$
$latex a=26-(11)6$
$latex a=26-66$
$latex a=-40$
EJEMPLO 4
Encuentra el primer término de una progresión aritmética en la que el término 6 es igual a 20 y el término 3 es igual a 11.
Solución
En este caso, no conocemos la diferencia común directamente. Sin embargo, tenemos los valores de dos términos diferentes, junto con sus posiciones:
- $latex a_{6}=20$
- $latex a_{3}=11$
Podemos encontrar la diferencia común al restar el valor del término 6 por el valor del término 3 y dividir por la diferencia de las posiciones, es decir, 6-3=3.
$$d=\frac{20-11}{6-3}$$
$$d=\frac{9}{3}=3$$
Ahora, usamos la diferencia común para encontrar el valor del primer término (podemos usar el término $latex a_{6}$ o $latex a_{3}$):
$latex a=a_{n}-(n-1)d$
$latex a=11-(3-1)3$
$latex a=11-(2)3$
$latex a=11-6$
$latex a=5$
EJEMPLO 5
Una progresión aritmética tiene los términos $latex a_{8}=45$ y $latex a_{4}=25$. ¿Cuál es el valor del primer término?
Solución
Similar al ejercicio anterior, no conocemos la diferencia común, pero conocemos los valores de dos términos de la progresión:
- $latex a_{8}=45$
- $latex a_{4}=25$
Entonces, encontramos la diferencia común al restar a los valores de los términos y dividir por la diferencia de las posiciones de los términos:
$$d=\frac{45-25}{8-4}$$
$$d=\frac{20}{4}=5$$
Ahora, podemos encontrar el valor del primer término de la progresión aritmética:
$latex a=a_{n}-(n-1)d$
$latex a=25-(4-1)5$
$latex a=25-(3)5$
$latex a=25-15$
$latex a=10$
EJEMPLO 6
Encuentra el primer término de una progresión aritmética en la que el término 25 es igual a -100 y el término 10 es igual a -10.
Solución
Tenemos los valores de los siguientes términos:
- $latex a_{25}=-100$
- $latex a_{10}=-10$
Entonces, encontramos la diferencia común al restar los valores de los términos y dividir por la diferencia de las posiciones de los términos:
$$d=\frac{-100-(-10)}{25-10}$$
$$d=\frac{-90}{15}=-6$$
Usando cualquiera de los términos y la diferencia común encontrada, podemos determinar el valor del primer término de la progresión:
$latex a=a_{n}-(n-1)d$
$latex a=-10-(10-1)-6$
$latex a=-10-(9)-6$
$latex a=-10+54$
$latex a=44$
Primer término de progresiones aritméticas – Ejercicios para resolver
Encuentra el primer término de una progresión aritmética en la que el término 7 es igual a 10 y el término 12 es igual a -25.
Escribe la respuesta en la casilla.
Véase también
¿Interesado en aprender más sobre progresiones aritméticas? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
