La suma de una progresión aritmética puede ser encontrada usando dos fórmulas diferentes dependiendo de la información que tenemos disponible. Generalmente, la información esencial es el valor del primer término, el número de términos y el último término o la diferencia común.
A continuación, resolveremos varios ejercicios de la suma de progresiones aritméticas. Además, veremos algunos ejercicios prácticos en los que podrás aplicar lo aprendido.
ÁLGEBRA
Relevante para…
Resolver algunos ejercicios de suma de progresiones aritméticas.
ÁLGEBRA
Relevante para…
Resolver algunos ejercicios de suma de progresiones aritméticas.
Fórmulas para la suma de una progresión aritmética
Las progresiones aritméticas son progresiones en las que sus términos son formados del término anterior al sumar un cierto número llamado la diferencia común.
La suma de los primeros $latex n$ términos de una progresión aritmética puede ser encontrada con la siguiente fórmula
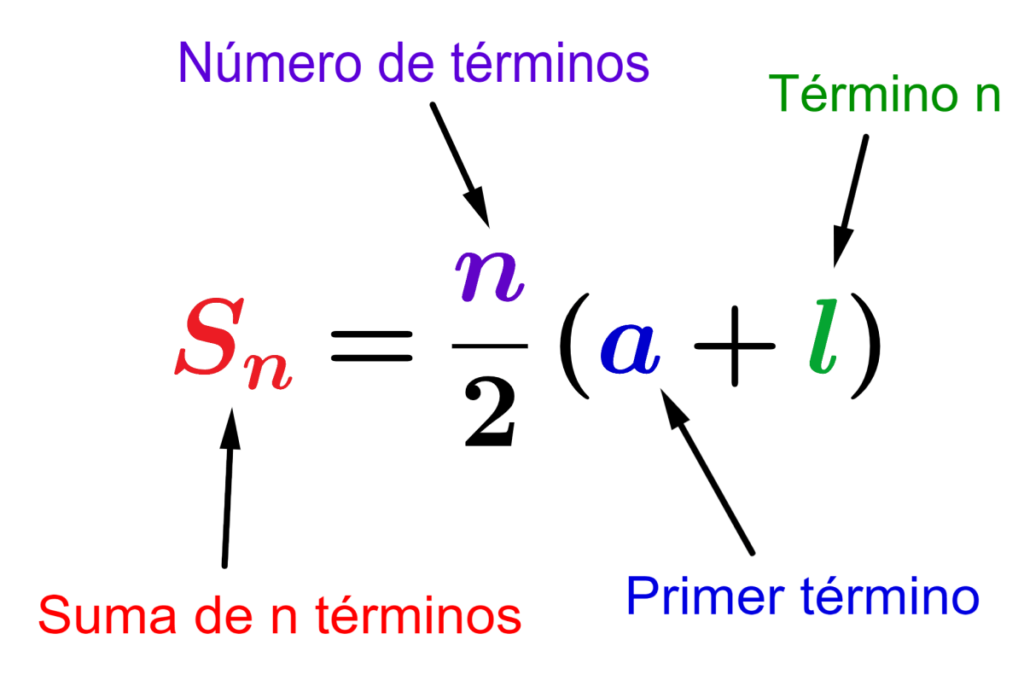
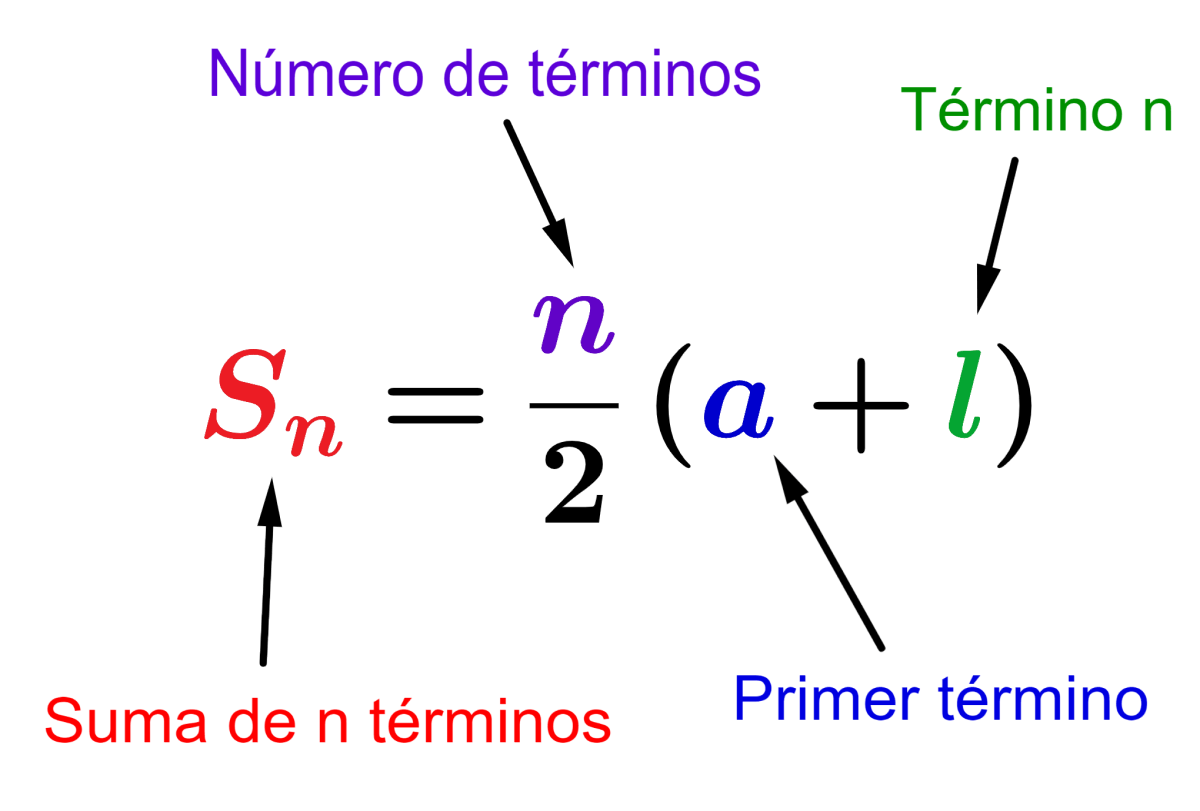
$$S_{n}=\frac{n}{2}(a+l)$$
en donde,
- $latex a$ es el primer término de la progresión.
- $latex l$ es el último término.
- $latex n $ es el número de términos.
Además, recordando que cualquier término de una progresión aritmética puede ser encontrado usando la fórmula $latex a_{n}=a+(n-1)d$, podemos escribir a la fórmula de la suma de la siguiente forma:
$$S_{n}=\frac{n}{2}[2a+(n-1)d]$$
en donde,
- $latex a$ es el primer término.
- $latex d$ es la diferencia común.
- $latex n $ es el número de términos.
Demostración de la fórmula de la suma de progresiones aritméticas
Recordemos que cada término de una progresión aritmética es obtenido al sumar la diferencia común, d, al término previo. Entonces, podemos escribir lo siguiente:
$$S_{n}=a+[a+d]+…+[a+(n-1)d]$$
Esta es la ecuación [1]. Ahora, escribimos a los términos en orden reverso, es decir, desde la derecha hacia la izquierda.
$$S_{n}=[a+(n-1)d]+[a+(n-2)d]+…+a$$
Esta es la ecuación [2]. Si es que sumamos ambas ecuaciones, podemos obtener el valor de $latex 2S_{n}$:
$$2S_{n}=(a+[a+(n-1)d])+((a+d)+[a+(n-2)d])+…+([a+(n-1)d]+a)$$
$$2S_{n}=[2a+(n-1)d]+[2a+(n-1)d]+…+[2a+(n-1)d]$$
Podemos observar que los términos obtenidos son iguales, por lo que la suma es igual a uno de los términos multiplicados por n (número total de términos).
$$2S_{n}=n[2a+(n-1)d]$$
Por último, dividimos a toda la ecuación para encontrar $latex S_{n}$:
$$S_{n}=\frac{n}{2}[2a+(n-1)d]$$
10 Ejercicios resueltos de sumas de progresiones aritméticas
EJERCICIO 1
Encuentra la suma de los primeros 8 términos de una progresión aritmética en la que el primer término es 4 y el término 8 es 25.
Solución
Podemos empezar por escribir todos los valores que conocemos:
- Primer término: $latex a=4$
- Último término: $latex l=8$
- Número de términos: $latex n=8$
Ahora, podemos usar la fórmula de la suma de progresiones aritméticas con los valores dados:
$$S_{n}=\frac{n}{2}[a+l]$$
$$S_{8}=\frac{8}{2}[4+25]$$
$$S_{8}=4[29]$$
$$S_{8}=116$$
EJERCICIO 2
El primer término de una progresión aritmética es 7 y el término 15 es 63. Encuentra la suma de los 15 primeros términos.
Solución
Empezamos escribiendo a todos los valores conocidos:
- Primer término: $latex a=7$
- Último término: $latex l=63$
- Número de términos: $latex n=15$
Ahora, usamos la fórmula de la suma de una progresión aritmética:
$$S_{n}=\frac{n}{2}[a+l]$$
$$S_{15}=\frac{15}{2}[7+63]$$
$$S_{15}=7.5[70]$$
$$S_{15}=525$$
EJERCICIO 3
Encuentra la suma de los 9 primeros términos de una progresión aritmética en la que el primer término es -20 y el término 9 es -44.
Solución
Tenemos la siguiente información:
- $latex a=-20$
- $latex l=-44$
- $latex n=9$
Usando la fórmula de la suma con la información dada, tenemos:
$$S_{n}=\frac{n}{2}[a+l]$$
$$S_{9}=\frac{9}{2}[-20-44]$$
$$S_{9}=4.5[-64]$$
$$S_{9}=-288$$
EJERCICIO 4
Encuentra la suma de los primeros 20 términos de una progresión aritmética que empieza con 5, 9, 13, 17, …
Solución
En este caso, no conocemos al término 20 de la progresión. Sin embargo, podemos encontrar la diferencia común al restar a un término por su término previo.
Entonces, tenemos 9-5=4. Y tenemos la siguiente información:
- Primer término: $latex a=5$
- Diferencia común: $latex d=4$
- Número de términos: $latex n=20$
Ahora, usamos esta información en la segunda fórmula de la suma de una progresión aritmética:
$$S_{n}=\frac{n}{2}[2a+(n-1)d]$$
$$S_{20}=\frac{20}{2}[2(5)+(20-1)4]$$
$$=10[10+(19)4]$$
$latex =10[10+76]$
$latex =10(86)$
$latex S_{20}=860$
EJERCICIO 5
Una progresión aritmética empieza con los términos 60, 55, 50, … Encuentra la suma de los primeros 12 términos.
Solución
Podemos encontrar la diferencia común al restar a un término por su término previo: 55-60=-5. Entonces, tenemos lo siguiente:
- $latex a=60$
- $latex d=-5$
- $latex n=12$
Ahora, podemos usar la segunda fórmula de la suma de una progresión aritmética con la información dada:
$$S_{n}=\frac{n}{2}[2a+(n-1)d]$$
$$S_{12}=\frac{12}{2}[2(60)+(12-1)(-5)]$$
$$=6[120+(11)(-5)]$$
$latex =6[120-55]$
$latex =6(65)$
$latex S_{12}=390$
EJERCICIO 6
Encuentra la suma de los primeros 25 términos de una progresión aritmética que empieza con los términos 9, -1, -11, …
Solución
La diferencia común de la progresión es -1-9=-10. Entonces, tenemos los siguientes valores:
- $latex a=9$
- $latex d=-10$
- $latex n=25$
Ahora, vamos a usar la segunda fórmula de la suma de una progresión aritmética:
$$S_{n}=\frac{n}{2}[2a+(n-1)d]$$
$$S_{25}=\frac{25}{2}[2(9)+(25-1)(-10)]$$
$$=12.5[18+(24)(-10)]$$
$latex =12.5[18-240]$
$latex =12.5(-222)$
$latex S_{25}=2775$
EJERCICIO 7
¿Cuál es el resultado de la siguiente suma de la progresión aritmética?
$$6+8+10+…30$$
Solución
Podemos empezar encontrando la diferencia común de la progresión: 8-6=2. Entonces, tenemos:
- Primer término: $latex a=6$
- Diferencia común: $latex d=2$
- Último término: $latex l=30$
No tenemos el número de términos, por lo que podemos usar la fórmula del término general para encontrarlo:
$latex a_{n}=a+(n-1)d$
$latex 30=6+(n-1)2$
$latex 24=(n-1)2$
$latex 12=n-1$
$latex n=13$
Ahora que tenemos toda la información requerida, podemos usar la fórmula de la suma de progresiones aritméticas:
$$S_{n}=\frac{n}{2}[a+l]$$
$$S_{13}=\frac{13}{2}[6+30]$$
$$S_{13}=\frac{13}{2}[36]$$
$$S_{13}=234$$
EJERCICIO 8
Encuentra la suma de la siguiente progresión aritmética:
$$9+13+17+…+41$$
Solución
La diferencia común es igual a 13-9=4. Entonces, tenemos los siguientes valores:
- $latex a=9$
- $latex d=4$
- $latex l=41$
Ahora, usamos la fórmula del término general para encontrar el valor de n:
$latex a_{n}=a+(n-1)d$
$latex 41=9+(n-1)4$
$latex 32=(n-1)4$
$latex 8=n-1$
$latex n=9$
Ahora que tenemos toda la información requerida, podemos encontrar la suma de la progresión:
$$S_{n}=\frac{n}{2}[a+l]$$
$$S_{9}=\frac{9}{2}[9+41]$$
$$S_{9}=\frac{9}{2}[50]$$
$$S_{9}=225$$
EJERCICIO 9
¿Cuál es el resultado de la suma de la siguiente progresión aritmética?
$$62+60+58+…+38$$
Solución
La diferencia común de la progresión es igual a 60-62=-2. Entonces, tenemos los siguientes valores:
- $latex a=62$
- $latex d=-2$
- $latex l=38$
Ahora, vamos a usar la fórmula del término general para encontrar el valor de n:
$latex a_{n}=a+(n-1)d$
$latex 38=62+(n-1)(-2)$
$latex -24=(n-1)(-2)$
$latex 12=n-1$
$latex n=13$
Ahora, encontramos la suma con estos datos:
$$S_{n}=\frac{n}{2}[a+l]$$
$$S_{13}=\frac{13}{2}[62+38]$$
$$S_{13}=\frac{13}{2}[100]$$
$$S_{13}=650$$
EJERCICIO 10
Si es que el primer término de una progresión aritmética es 2 y el término n es 32, encuentra el valor de n si es que la suma de los primeros n términos es 357.
Solución
Podemos usar la fórmula del término general con $latex a_{n}=32$:
$latex a+(n-1)d=32$
Además, dado que sabemos que el primer término es 2, tenemos:
$latex 2+(n-1)d=32$
$latex (n-1)d=30~~[1]$
Ahora, usamos la fórmula de la suma con el valor $latex S_{n}=357$:
$$ \frac{n}{2}[2a+(n-1)d]=357$$
Dado que sabemos que $latex a=2$, tenemos:
$$ \frac{n}{2}[2(2)+(n-1)d]=357$$
$$ \frac{n}{2}[4+(n-1)d]=357~~[2]$$
Substituyendo la ecuación [1] en la ecuación [2], tenemos:
$latex n(4+30)=714$
$latex 34n=714$
$latex n=21$
Ejercicios de suma de progresiones aritméticas para resolver
¿Cuál es el resultado de la siguiente suma de una progresión aritmética? $$1.3+1.6+1.9+…+4.6$$
Escribe la respuesta en la casilla.
Véase también
¿Interesado en aprender más sobre progresiones aritméticas? Puedes mirar estas páginas: