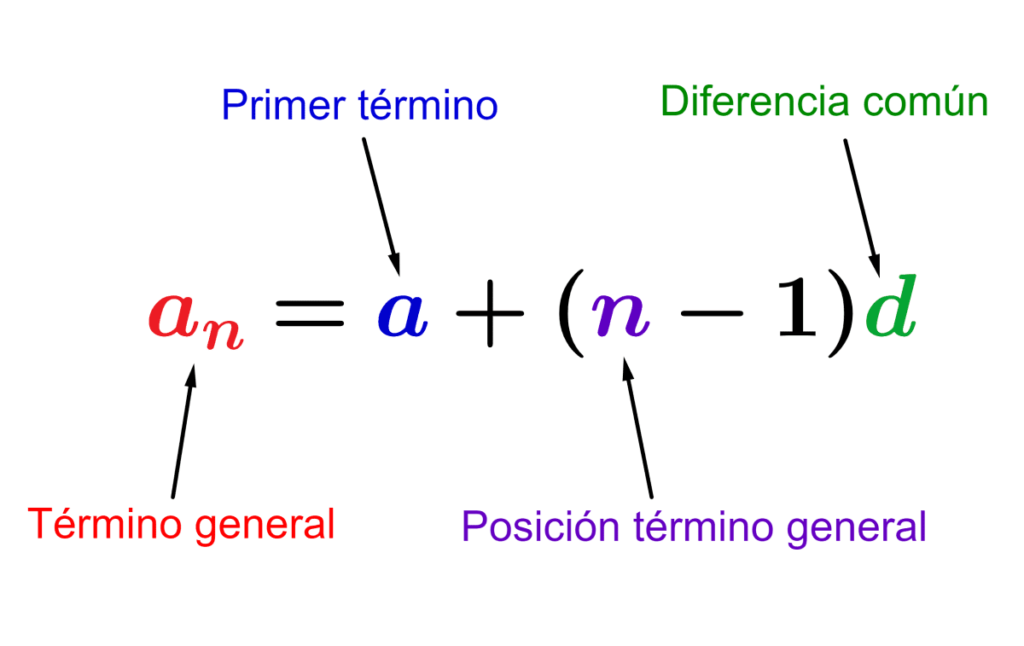
El término general de una progresión aritmética es encontrado usando el valor de la diferencia común, la posición del término y el valor del primer término. Entonces, restamos 1 de la posición del término y multiplicamos por la diferencia común. Luego, sumamos el valor del primer término para encontrar el término general.
A continuación, resolveremos algunos ejercicios del término general de progresiones aritméticas. Además, podrás practicar tus conocimientos de este tema con ejercicios para resolver.
Pasos para encontrar el término general de una progresión aritmética
Consideremos la progresión de números 1, 3, 5, 7, … Cada término de esta progresión es obtenido al sumar 2 al término anterior. Este es el ejemplo de una progresión aritmética.
Las progresiones aritméticas son progresiones en las que cualquier término es formado del término anterior al sumar un cierto número llamado la diferencia común.
Generalmente, los términos de una progresión aritmética pueden ser obtenidos usando la siguiente fórmula:
$$a_{n}=a+(n-1)d$$
en donde,
- $latex a$ es el primer término de la progresión.
- $latex d$ es la diferencia común.
- $latex n $ es la posición del término.

Entonces, podemos seguir los siguientes pasos para encontrar el término general de una progresión aritmética.
1. Encontrar el valor del primer término.
2. Encontrar el valor de la diferencia común.
La diferencia común es encontrada al restar a un término de la progresión por el término previo.
3. Usar la fórmula del término general.
Sustituimos los valores del primer término, la diferencia común y la posición del término en la fórmula $latex a_{n}=a+(n-1)d$.
10 Ejercicios resueltos de término general de progresiones aritméticas
EJERCICIO 1
Encuentra el valor del término 6 de una progresión aritmética que tiene un valor inicial de 2 y una diferencia común de 3.
Solución
En este ejercicio, conocemos los valores del valor inicial y la diferencia común directamente. Además, sabemos que tenemos que encontrar el término 6. Entonces,
- Primer término: $latex a=2$
- Diferencia común: $latex d=3$
- Posición término: $latex n=6$
Usando estos valores en la fórmula del término general de una progresión aritmética, tenemos:
$latex a_{n}=a+(n-1)d$
$latex a_{6}=2+(6-1)3$
$latex a_{6}=2+(5)3$
$latex a_{6}=2+15$
$latex a_{6}=17$
EJERCICIO 2
¿Cuál es el valor del término 8 de una progresión aritmética en la que el primer término es 4 y su diferencia común es 5?
Solución
Similar al ejercicio anterior, aquí también conocemos los valores del primer término y de la diferencia común. Entonces, tenemos:
- $latex a=4$
- $latex d=5$
- $latex n=8$
Al aplicar estos valores en la fórmula del término general de una progresión aritmética, tenemos:
$latex a_{n}=a+(n-1)d$
$latex a_{8}=4+(8-1)5$
$latex a_{8}=4+(7)5$
$latex a_{8}=4+35$
$latex a_{8}=39$
EJERCICIO 3
Si es que el primer término de una progresión aritmética es 10 y su diferencia común es -2, encuentra el valor del término 8.
Solución
Usando la información dada, podemos identificar los siguientes valores:
- $latex a=10$
- $latex d=-2$
- $latex n=8$
En este caso, tenemos una diferencia común negativa. Sin embargo, podemos usar la misma fórmula, ya que también aplica en estos casos:
$latex a_{n}=a+(n-1)d$
$latex a_{8}=10+(8-1)(-2)$
$latex a_{8}=10+(7)(-2)$
$latex a_{8}=10-14$
$latex a_{8}=-4$
EJERCICIO 4
Los primeros cuatro términos de una progresión aritmética son 3, 6, 9, 12. ¿Cuál es el valor del término 11 de la progresión?
Solución
En este ejercicio, conocemos el valor del primer término directamente, pero no la diferencia común.
Para encontrar la diferencia común, podemos restar a cualquier término por su término previo. Por ejemplo, tenemos $latex 12-9=3$. Entonces,
- $latex a=3$
- $latex d=3$
- $latex n=11$
Al usar estos valores con la fórmula del término general, tenemos:
$latex a_{n}=a+(n-1)d$
$latex a_{11}=3+(11-1)3$
$latex a_{11}=3+(10)3$
$latex a_{11}=3+30$
$latex a_{11}=33$
EJERCICIO 5
Los primeros cuatro términos de una progresión aritmética son 10, 6, 2, -2. Encuentra el término 8 de la progresión.
Solución
Empezamos encontrando el valor de la diferencia común. Entonces, tenemos $latex -2-2=-4$. Por lo tanto, tenemos lo siguiente:
- $latex a=10$
- $latex d=-4$
- $latex n=8$
Aplicando la fórmula del término general con estos valores, tenemos:
$latex a_{n}=a+(n-1)d$
$latex a_{8}=10+(8-1)(-4)$
$latex a_{8}=10+(7)(-4)$
$latex a_{8}=10-28$
$latex a_{8}=-18$
EJERCICIO 6
Una progresión aritmética empieza con los términos 3, 9, 15, … Encuentra el término 9 de la progresión.
Solución
Encontrando la diferencia común, tenemos $latex 15-9=6$. Entonces, tenemos los siguientes valores:
- $latex a=3$
- $latex d=6$
- $latex n=9$
Usando estos valores en la fórmula del término general, tenemos:
$latex a_{n}=a+(n-1)d$
$latex a_{9}=3+(9-1)6$
$latex a_{9}=3+(8)6$
$latex a_{9}=3+48$
$latex a_{9}=51$
EJERCICIO 7
Encuentra el término 12 de la progresión aritmética que empieza con los términos 12, 7, 2, …
Solución
El valor de la diferencia común es $latex 2-7=-5$. Entonces, observamos los siguientes valores:
- $latex a=12$
- $latex d=-5$
- $latex n=12$
Al usar estos valores con la fórmula del término general, tenemos:
$latex a_{n}=a+(n-1)d$
$latex a_{12}=12+(12-1)(-5)$
$latex a_{12}=12+(11)(-5)$
$latex a_{12}=12-55$
$latex a_{12}=-43$
EJERCICIO 8
Una progresión aritmética empieza con los términos -13, -9, -5, … ¿Cuál es el valor del término 7?
Solución
La diferencia común de la progresión dada es $latex -5-(-9)=4$. Entonces, tenemos:
- $latex a=-13$
- $latex d=4$
- $latex n=7$
Aplicando la fórmula del término general con estos valores, tenemos:
$latex a_{n}=a+(n-1)d$
$latex a_{7}=-13+(7-1)4$
$latex a_{7}=-13+(6)4$
$latex a_{7}=-13+24$
$latex a_{7}=11$
EJERCICIO 9
Una progresión aritmética tiene los primeros cuatro términos: 5, 11, 17, 23. Encuentra el término 30.
Solución
La diferencia común de la progresión dada es $latex 23-17=6$. Por lo tanto, tenemos la siguiente información:
- $latex a=5$
- $latex d=6$
- $latex n=30$
Usando la fórmula del término general con estos valores, tenemos:
$latex a_{n}=a+(n-1)d$
$latex a_{30}=5+(30-1)6$
$latex a_{30}=5+(29)6$
$latex a_{30}=5+174$
$latex a_{30}=179$
EJERCICIO 10
Encuentra el término 26 de la progresión aritmética que empieza con los números 20, 17, 14, …
Solución
La diferencia común de la progresión dada es $latex 14-17=-3$. Entonces, tenemos los siguientes valores:
- $latex a=20$
- $latex d=-3$
- $latex n=26$
Usando la fórmula con los valores dados, tenemos:
$latex a_{n}=a+(n-1)d$
$latex a_{26}=20+(26-1)(-3)$
$latex a_{26}=20+(25)(-3)$
$latex a_{26}=20-75$
$latex a_{26}=-55$
Ejercicios de término general de progresiones aritméticas para resolver


¿Cuál es el término 16 de una progresión aritmética que empieza con los términos 19, 12, 5, …?
Escribe la respuesta en la casilla.
Véase también
¿Interesado en aprender más sobre progresiones aritméticas? Puedes mirar estas páginas: